第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 在公园的$O处附近有E$,$F$,$G$,$H$四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以$O$为圆心,$OA$为半径的圆形水池,要求池中不留树木,则$E$,$F$,$G$,$H$四棵树中需要被移除的为(
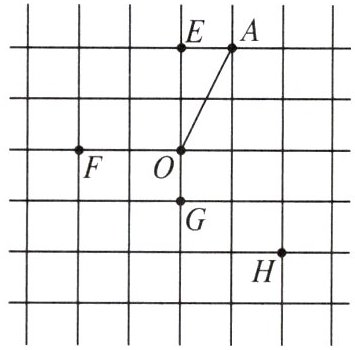
A.$E$,$F$,$G$
B.$F$,$G$,$H$
C.$G$,$H$,$E$
D.$H$,$E$,$F$
A
)
A.$E$,$F$,$G$
B.$F$,$G$,$H$
C.$G$,$H$,$E$
D.$H$,$E$,$F$
答案:
A
2. 下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有(
A.$1$个
B.$2$个
C.$3$个
D.$4$个
B
)A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
B
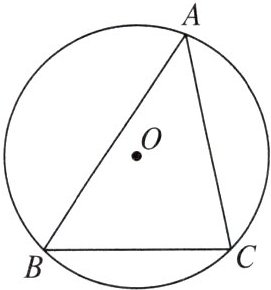
3. 如图,$\odot O是\triangle ABC$的外接圆,$\angle A = 45^{\circ}$,$BC = 4$,则$\odot O$的直径为
4√2
。
答案:
4√2
4. 用反证法证明“在一个三角形中,至少有一个内角大于或等于$60^{\circ}$”时,可先假设“
三角形的三个内角都小于60°
”,然后经证明与“三角形内角和定理
”相矛盾,所以原命题成立。
答案:
三角形的三个内角都小于60° 三角形内角和定理
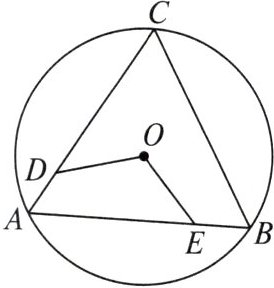
5. 如图,$\triangle ABC是\odot O$的内接正三角形,点$O$是圆心,点$D$,$E分别在边AC$,$AB$上,若$DA = EB$,则$\angle DOE$的度数是
120
度。
答案:
120
1. 用反证法证明“两条直线相交只有一个交点”应该先假设(
A.两条直线相交至少有两个交点
B.两条直线相交没有两个交点
C.两条直线平行时也有一个交点
D.两条直线平行没有交点
A
)A.两条直线相交至少有两个交点
B.两条直线相交没有两个交点
C.两条直线平行时也有一个交点
D.两条直线平行没有交点
答案:
A
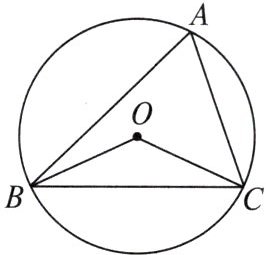
2. 有一题目:“已知点$O为\triangle ABC$的外心,$\angle BOC = 130^{\circ}$,求$\angle A$。”嘉嘉的解答为:画$\triangle ABC以及它的外接圆O$,连接$OB$,$OC$,如图所示。由$\angle BOC = 2\angle A = 130^{\circ}$,得$\angle A = 65^{\circ}$。而淇淇说:“嘉嘉考虑的不周全,$\angle A$还应有另一个不同的值。”下列判断正确的是(
A.淇淇说的对,且$\angle A的另一个值是115^{\circ}$
B.淇淇说的不对,$\angle A就得65^{\circ}$
C.嘉嘉求的结果不对,$\angle A应得50^{\circ}$
D.两人都不对,$\angle A应有3$个不同的值
A
)
A.淇淇说的对,且$\angle A的另一个值是115^{\circ}$
B.淇淇说的不对,$\angle A就得65^{\circ}$
C.嘉嘉求的结果不对,$\angle A应得50^{\circ}$
D.两人都不对,$\angle A应有3$个不同的值
答案:
A
3. 如图,在平面直角坐标系中,点$A$,$B$,$C的坐标分别为(1,4)$,$(5,4)$,$(1,-2)$,则$\triangle ABC$外接圆的圆心坐标是(
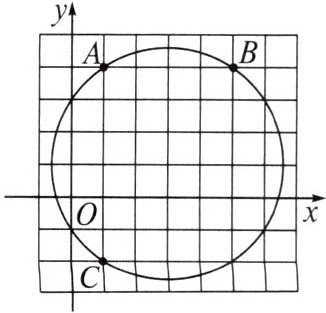
A.$(2,3)$
B.$(3,2)$
C.$(1,3)$
D.$(3,1)$
D
)
A.$(2,3)$
B.$(3,2)$
C.$(1,3)$
D.$(3,1)$
答案:
D
查看更多完整答案,请扫码查看


