第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 把一个平面图形绕着平面内某一点 $ O $ 转动一个角度,叫做图形的
旋转
,点 $ O $ 叫做旋转中心
,转动的角叫做旋转角
。如果图形上的点 $ P $ 经过旋转变为点 $ P' $,那么这两个点叫做这个旋转的对应点
。
答案:
1.旋转 旋转中心 旋转角 对应点
2. 钟表的分针匀速旋转一周需要 $ 60 \min $,钟表的轴心是它的____,经过 $ 20 \min $,分针的旋转角为____度。
答案:
2.旋转中心 120
3. 旋转的性质:
(1)对应点到旋转中心的距离____;
(2)对应点与旋转中心所连线段的夹角等于____;
(3)旋转前、后的图形____。
(1)对应点到旋转中心的距离____;
(2)对应点与旋转中心所连线段的夹角等于____;
(3)旋转前、后的图形____。
答案:
3.
(1)相等
(2)旋转角
(3)全等
(1)相等
(2)旋转角
(3)全等
4. 如图,以点 $ O $ 为旋转中心,将 $ \angle 1 $ 按顺时针方向旋转 $ 110^{\circ} $,得到 $ \angle 2 $。若 $ \angle 1 = 40^{\circ} $,则 $ \angle 2 = $____,$ \angle 3 = $____。
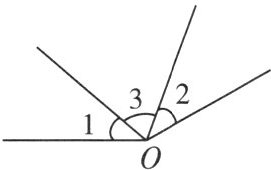

答案:
4.40° 70°
1. 下列几种运动:①单摆上小球的转动;②发电风车上扇叶的运动;③传送带上的物体;④笔直铁轨上飞驰而过的火车。其中属于旋转的有(
A.$ 0 $ 种
B.$ 1 $ 种
C.$ 2 $ 种
D.$ 3 $ 种
C
)A.$ 0 $ 种
B.$ 1 $ 种
C.$ 2 $ 种
D.$ 3 $ 种
答案:
C
2. 有两个直角三角形纸板,一个含 $ 45^{\circ} $ 角,另一个含 $ 30^{\circ} $ 角,按如图①所示方式叠放,先将含 $ 30^{\circ} $ 角的纸板固定不动,再将含 $ 45^{\circ} $ 角的纸板绕顶点 $ A $ 顺时针旋转,使 $ BC // DE $,如图②所示,则旋转角 $ \angle BAD $ 的度数为(
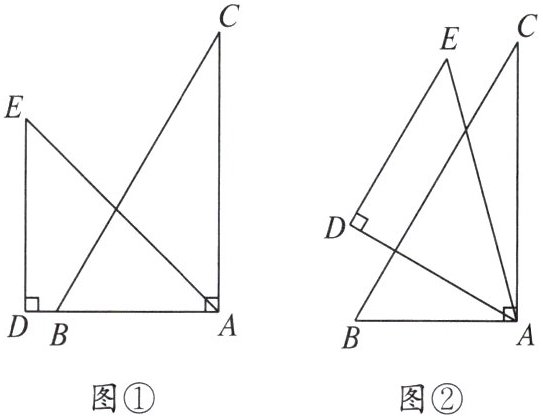
A.$ 15^{\circ} $
B.$ 30^{\circ} $
C.$ 45^{\circ} $
D.$ 60^{\circ} $
B
)
A.$ 15^{\circ} $
B.$ 30^{\circ} $
C.$ 45^{\circ} $
D.$ 60^{\circ} $
答案:
B
3. 下列四个三角形中,不能由 $ \triangle ABC $ 经过旋转或平移得到的是(
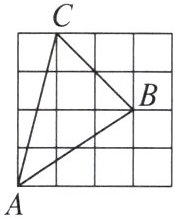
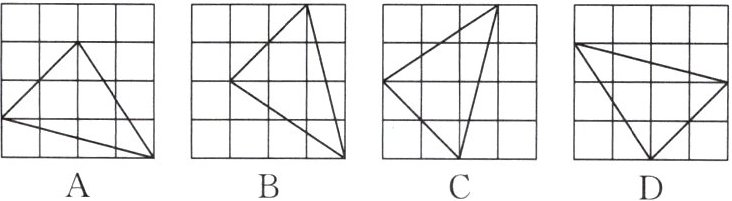
B
)

答案:
B
4. 如图,在等边三角形 $ ABC $ 中,$ D $ 是 $ AC $ 上一点,连接 $ BD $,将 $ \triangle BCD $ 绕点 $ B $ 逆时针旋转 $ 60^{\circ} $,得到 $ \triangle BAE $,连接 $ ED $,若 $ BC = 5 $,$ BD = 4 $,则下列结论错误的是(
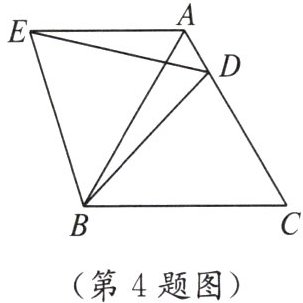
A.$ AE // BC $
B.$ \angle ADE = \angle BDC $
C.$ \triangle BDE $ 是等边三角形
D.$ \triangle ADE $ 的周长是 $ 9 $
B
)
A.$ AE // BC $
B.$ \angle ADE = \angle BDC $
C.$ \triangle BDE $ 是等边三角形
D.$ \triangle ADE $ 的周长是 $ 9 $
答案:
B
查看更多完整答案,请扫码查看


