《2025年同步测控优化设计九年级数学上册人教版精编版》

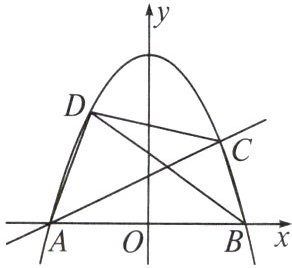
10. 如图,二次函数$y = -\frac{1}{2}x^{2}+c的图象经过点D(-\sqrt{3},\frac{9}{2})$,与$x轴交于A$,$B$两点.
(1)求$c$的值；
(2)设点$C为该二次函数的图象在x$轴上方的一点,直线$AC将四边形ABCD$的面积二等分,试证明线段$BD被直线AC$平分,并求此时直线$AC$的函数解析式.

答案：
分析：
(1)将点D的坐标代入二次函数解析式即可求出c的值；
(2)要证明线段BD被直线AC平分，从“直线AC将四边形ABCD的面积二等分”来寻求解题思路，不难发现S_{△ABC}=S_{△ADC}，通过面积法可得公共边AC上的两条高相等，再通过全等可得线段BD被直线AC平分.
解：
(1)因为抛物线经过点D(−$\sqrt{3}$,$\frac{9}{2}$)，所以−$\frac{1}{2}$×(−$\sqrt{3}$)²+c=$\frac{9}{2}$.所以c=6.
(2)如图，过点D、B分别作直线AC的垂线，垂足分别为E、F，设AC与BD交于点M.

因为直线AC将四边形ABCD的面积二等分，即S_{△ABC}=S_{△ADC}，所以DE=BF.
又因为∠DME=∠BMF，∠DEM=∠BFM，所以△DEM≌△BFM.所以DM=BM，即直线AC平分线段BD.
因为c=6，所以抛物线的解析式为y=−$\frac{1}{2}$x²+6.
所以A(−2$\sqrt{3}$,0)，B(2$\sqrt{3}$,0).
因为直线AC平分线段BD，即M是线段BD的中点，所以M($\frac{\sqrt{3}}{2}$,$\frac{9}{4}$).
设直线AC的解析式为y=kx+b，由直线AC经过点A、M，可得$\begin{cases}-2\sqrt{3}k + b = 0\frac{\sqrt{3}}{2}k + b = \frac{9}{4}\end{cases}$
解得$\begin{cases}k = \frac{3\sqrt{3}}{10}\\b = \frac{9}{5}\end{cases}$
所以直线AC的解析式为y=$\frac{3\sqrt{3}}{10}$x+$\frac{9}{5}$.

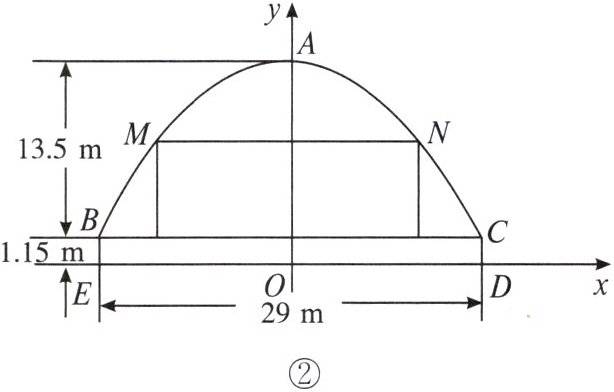
11. 某大剧场的上部为能够旋转的拱形钢结构,并且具有开启、闭合功能,如图①所示.舞台顶部横剖面拱形可近似看作抛物线的一部分,其中舞台高度为$1.15m$,台口高度为$13.5m$,台口宽度为$29m$,如图②所示.以$ED所在直线为x$轴,过拱顶点$A且垂直于ED的直线为y$轴,建立平面直角坐标系.


(1)求拱形抛物线的函数解析式；
(2)舞台大幕悬挂在长度为$20m的横梁MN$上,其下沿恰与舞台面接触,求大幕的高度(精确到$0.01m$).

答案： 解：
(1)由题设可知，OA=13.5+1.15=14.65(m)，OD=$\frac{29}{2}$(m)，则A(0,14.65)，C($\frac{29}{2}$,1.15).
设拱形抛物线的解析式为y=ax²+c，则$\begin{cases}14.65 = a·0² + c\\1.15 = a·(\frac{29}{2})² + c\end{cases}$
解得a=−$\frac{54}{841}$，c=14.65.故所求函数的解析式为y=−$\frac{54}{841}$x²+14.65.
(2)由MN=20m，设点N的坐标为(10,y₀)，代入关系式，得y₀=−$\frac{54}{841}$×10²+14.65≈8.229.
故y₀−1.15=8.229−1.15=7.079≈7.08，即大幕的高度约为7.08m.