《2025年同步测控优化设计九年级数学上册人教版精编版》

2. 一座拱桥的轮廓是抛物线形(如图①),拱高为 $ 6 \ m $,跨度为 $ 20 \ m $,相邻两支柱间的距离均为 $ 5 \ m $.

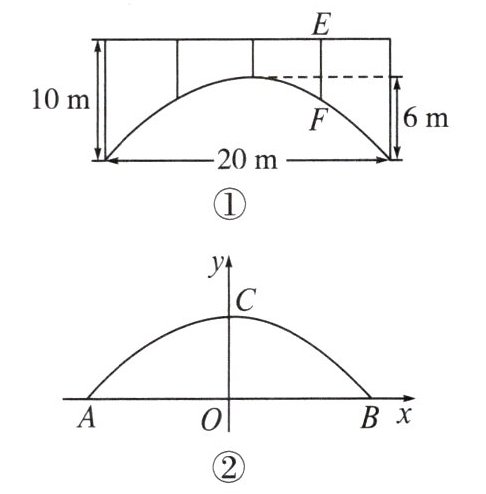
(1) 将抛物线放在所给的平面直角坐标系中(如图②),求抛物线的解析式；
(2) 求支柱 $ EF $ 的长度；
(3) 拱桥下地平面是双向行车道(正中间是一条宽 $ 2 \ m $ 的隔离带),其中的一条行车道能否并排行驶宽为 $ 2 \ m $,高为 $ 3 \ m $ 的三辆汽车(汽车间的间隔忽略不计)？请说明你的理由.

答案：
2.解
(1)根据题目条件，A,B,C的坐标分别是(-10,0),(10,0),(0,6).设抛物线的解析式为y=ax²+c,将B,C的坐标代入y=ax²+c，得{c=6,100a+c=0,解得{a=-3/50,c=6.所以抛物线的解析式是y=-3/50x²+6.
(2)可设F(5,yF)，于是yF=-3/50×5²+6=4.5.从而支柱EF的长度是10 - 4.5 = 5.5(m).
(3)如图，设DN是隔离带的宽，NG的长是三辆车的宽度和，则点G坐标是(7,0).过点G作GH⊥AB交抛物线于点H,则yH=-3/50×7²+6≈3.06＞3.根据抛物线的特点，可知一条行车道能并排行驶这样的三辆汽车

3. 如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点 $ O $ 落在水平面上,对称轴是水平线 $ OC $. 点 $ A $,$ B $ 在抛物线上,且点 $ A $ 到水平面的距离 $ AC = 4 \ m $,点 $ B $ 到水平面的距离为 $ 2 \ m $,$ OC = 8 \ m $.

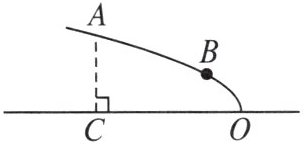
(1) 请建立适当的平面直角坐标系,求抛物线的函数解析式；
(2) 为了安全美观,现需在水平线 $ OC $ 上找一点 $ P $,如果用质地、规格已确定的圆形钢管制作两根支柱 $ PA $,$ PB $ 对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点 $ P $？(无须证明)
(3) 为了施工方便,如果现需计算出点 $ O $,$ P $ 之间的距离,那么两根支柱用料最省时,点 $ O $,$ P $ 之间的距离是多少？(请写出求解过程)

答案：
3.分析此题考查了二次函数的实际应用问题.解此题的关键是根据题意构建二次函数模型，根据二次函数解题.
(1)以点O为原点、射线OC为y轴的正半轴建立平面直角坐标系，可设抛物线的函数解析式为y=ax²，又由点A在抛物线上，即可求得此抛物线的函数解析式;
(2)延长AC,交建筑物造型所在抛物线于点D,连接BD交OC于点P，则点P即为所求;
(3)首先根据题意求得点B与点D的坐标，设直线BD的函数解析式为y=kx+b,利用待定系数法即可求得直线BD的函数解析式，把x=0代入求出的解析式，即可求得点P的坐标.解
(1)如图，以点O为原点、射线OC为y轴的正半轴建立平面直角坐标系，设抛物线的函数解析式为y=ax²，由题意知点A的坐标为(4,8). 因为点A在抛物线上,所以8=4²a,解得a=1/2.所以所求抛物线的函数解析式为y=1/2x².
(2)找法：延长AC,交抛物线于点D,则点A,D关于OC 对称,连接BD交OC于点P，则点P即为所求.
(3)由题意知，点B的横坐标为2,因为点B在抛物线上，所以点B的坐标为(2,2).又点A的坐标为(4,8)，所以点D的坐标为(-4,8).设直线BD的函数解析式为y=kx+b，则{2k+b=2,-4k+b=8,解得k=-1,b=4.所以直线BD的函数解析式为y=-x+4,把x=0代入y=-x+4,得点P的坐标为(0,4),因此两根支柱用料最省时，点O,P之间的距离是4m.