第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [中]如图,在△ABC 中,AB= 6,BC= 5,AC= 4,AD 平分∠BAC,交 BC 于点 D,在 AB 上截取 AE= AC,则△BDE 的周长为(

A.8
B.7
C.6
D.5
B
)
A.8
B.7
C.6
D.5
答案:
B 【解析】
∵ AD 平分∠BAC,
∴ ∠EAD = ∠CAD. 在△ADE 和△ADC 中,$\left\{\begin{array}{l} AE=AC,\\ ∠EAD=∠CAD,\\ AD=AD,\end{array}\right.$
∴ △ADE≌△ADC(SAS),
∴ ED = CD,
∴ BC = BD + CD = BD + DE = 5,
∴ △BDE 的周长为 BE + BD + ED = (6 - 4) + 5 = 7. 故选 B.
∵ AD 平分∠BAC,
∴ ∠EAD = ∠CAD. 在△ADE 和△ADC 中,$\left\{\begin{array}{l} AE=AC,\\ ∠EAD=∠CAD,\\ AD=AD,\end{array}\right.$
∴ △ADE≌△ADC(SAS),
∴ ED = CD,
∴ BC = BD + CD = BD + DE = 5,
∴ △BDE 的周长为 BE + BD + ED = (6 - 4) + 5 = 7. 故选 B.
2 新考法 [2025 四川成都期中,中]如图是由 9 个完全相同的小正方形拼接而成的 3×3 网格,图形 ABCD 中各个顶点均为格点,设∠ABC= α,∠BCD= β,∠BAD= γ,则 α-β-γ 的值为( )

A.45°
B.60°
C.75°
D.135°

A.45°
B.60°
C.75°
D.135°
答案:
A 【解析】如图,根据题意知,BE = AG,∠BEC = ∠AGB = 90°,EC = GB,
∴ △BEC≌△AGB(SAS),
∴ ∠ECB = ∠GBA.
∵ ∠ECB + ∠EBC = 90°,
∴ ∠GBA + ∠EBC = 90°,
∴ ∠ABC = 90° = α.
∵ ∠BCD + ∠CBD = β + ∠CBD = 90°,∠CBD + ∠ABD = 90°,
∴ ∠ABD = β.
∵ ∠ADF = ∠ABD + ∠BAD = 45°,
∴ β + γ = 45°,
∴ α - β - γ = α - (β + γ) = 90° - 45° = 45°,故选 A.

A 【解析】如图,根据题意知,BE = AG,∠BEC = ∠AGB = 90°,EC = GB,
∴ △BEC≌△AGB(SAS),
∴ ∠ECB = ∠GBA.
∵ ∠ECB + ∠EBC = 90°,
∴ ∠GBA + ∠EBC = 90°,
∴ ∠ABC = 90° = α.
∵ ∠BCD + ∠CBD = β + ∠CBD = 90°,∠CBD + ∠ABD = 90°,
∴ ∠ABD = β.
∵ ∠ADF = ∠ABD + ∠BAD = 45°,
∴ β + γ = 45°,
∴ α - β - γ = α - (β + γ) = 90° - 45° = 45°,故选 A.

3 [2024 江苏泰州期中,中]如图,在△ABC 中,∠B= ∠C,BE= CD,BD= CF,则∠EDF 等于(
A.90°- $\frac{1}{2}$∠A
B.∠A
C.90°+∠A
D.90°+ $\frac{1}{2}$∠A
A
)A.90°- $\frac{1}{2}$∠A
B.∠A
C.90°+∠A
D.90°+ $\frac{1}{2}$∠A
答案:
A 【解析】在△BDE 和△CFD 中,$\left\{\begin{array}{l} BE=CD,\\ ∠B=∠C,\\ BD=CF,\end{array}\right.$
∴ △BDE≌△CFD(SAS),
∴ ∠BDE = ∠CFD.
∵ ∠EDF = 180° - (∠BDE + ∠CDF) = 180° - (∠CFD + ∠CDF) = 180° - (180° - ∠C) = ∠C,且∠A + ∠B + ∠C = 180°,
∴ ∠A + 2∠EDF = 180°,
∴ ∠EDF = 90° - $\frac{1}{2}$∠A. 故选 A.
∴ △BDE≌△CFD(SAS),
∴ ∠BDE = ∠CFD.
∵ ∠EDF = 180° - (∠BDE + ∠CDF) = 180° - (∠CFD + ∠CDF) = 180° - (180° - ∠C) = ∠C,且∠A + ∠B + ∠C = 180°,
∴ ∠A + 2∠EDF = 180°,
∴ ∠EDF = 90° - $\frac{1}{2}$∠A. 故选 A.
4 [2025 江苏苏州调研,中]如图,已知 AB= AD,BC= DE,∠CAD= 12°,∠B= ∠D= 30°,∠EAB= 128°,则∠EGF 的度数为
110°
。
答案:
110° 【解析】在△ABC 和△ADE 中,$\left\{\begin{array}{l} AB=AD,\\ ∠B=∠D,\\ BC=DE,\end{array}\right.$
∴ △ABC≌△ADE(SAS),
∴ ∠CAB = ∠EAD.
∵ ∠CAD = 12°,∠EAB = 128°,
∴ ∠CAB = ∠EAD = $\frac{1}{2}$(∠EAB - ∠CAD) = 58°.
∵ ∠AFG = ∠DAB + ∠B = ∠CAD + ∠CAB + ∠B = 12° + 58° + 30° = 100°,∠E = 180° - ∠EAD - ∠D = 180° - 58° - 30° = 92°,
∴ ∠EGF = 360° - ∠E - ∠AFG - ∠EAD = 110°. 故答案为 110°.
∴ △ABC≌△ADE(SAS),
∴ ∠CAB = ∠EAD.
∵ ∠CAD = 12°,∠EAB = 128°,
∴ ∠CAB = ∠EAD = $\frac{1}{2}$(∠EAB - ∠CAD) = 58°.
∵ ∠AFG = ∠DAB + ∠B = ∠CAD + ∠CAB + ∠B = 12° + 58° + 30° = 100°,∠E = 180° - ∠EAD - ∠D = 180° - 58° - 30° = 92°,
∴ ∠EGF = 360° - ∠E - ∠AFG - ∠EAD = 110°. 故答案为 110°.
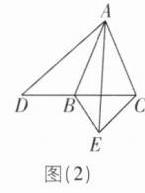
5 [2025 浙江杭州质检,较难]在△ABC 中,AB= AC,点 D 是直线 BC 上一点(不与 B,C 重合),以 AD 为一边在 AD 的右侧作△ADE,使 AD= AE,∠DAE= ∠BAC,连接 CE。

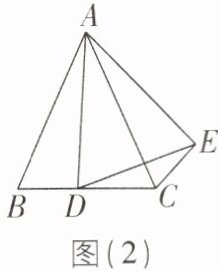
(1)如图(1),当点 D 在线段 BC 上时,若∠BAC= 90°,则∠BCE= ____°;
(2)如图(2),点 D 在直线 BC 上移动,若∠BAC= α,∠BCE= β,则 α 与 β 之间的数量关系为____。


(1)如图(1),当点 D 在线段 BC 上时,若∠BAC= 90°,则∠BCE= ____°;
(2)如图(2),点 D 在直线 BC 上移动,若∠BAC= α,∠BCE= β,则 α 与 β 之间的数量关系为____。
答案:
(1)90
(2)α+β=180°或α=β 【解析】
(1)
∵ ∠DAE = ∠BAC = 90°,
∴ ∠BAC - ∠DAC = ∠DAE - ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE.
∵ ∠BAC = 90°,
∴ ∠B + ∠ACB = 90°,
∴ ∠BCE = ∠ACE + ∠ACB = 90°.
(2)①当点 D 在线段 BC 上时,如题图
(2).
∵ ∠DAE = ∠BAC,
∴ ∠BAC - ∠DAC = ∠DAE - ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE. 在△ABC 中,∠BAC + ∠B + ∠ACB = 180°,
∴ ∠BAC + ∠ACE + ∠ACB = 180°,
∴ ∠BAC + ∠BCE = 180°.
∵ ∠BAC = α,∠BCE = β,
∴ α + β = 180°.
②当点 D 在 BC 的延长线上时,如图
(1).
∵ ∠DAE = ∠BAC,
∴ ∠BAC + ∠DAC = ∠DAE + ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE. 在△ABC 中,∠BAC + ∠B + ∠ACB = 180°,
∴ ∠BAC + ∠ACE + ∠ACB = 180°,
∴ ∠BAC + ∠BCE = 180°.
∵ ∠BAC = α,∠BCE = β,
∴ α + β = 180°.
③当点 D 在 CB 的延长线上时,如图
(2). 同理可得△BAD≌△CAE,
∴ ∠ABD = ∠ACE. 在△ABC 中,∠BAC + ∠ABC + ∠ACB = 180°,
∴ ∠BAC + 180° - ∠ABD + ∠ACE - ∠BCE = 180°,
∴ ∠BAC = ∠BCE.
∵ ∠BAC = α,∠BCE = β,
∴ α = β. 综上所述,α 与 β 之间的数量关系为 α + β = 180°或 α = β.

(1)90
(2)α+β=180°或α=β 【解析】
(1)
∵ ∠DAE = ∠BAC = 90°,
∴ ∠BAC - ∠DAC = ∠DAE - ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE.
∵ ∠BAC = 90°,
∴ ∠B + ∠ACB = 90°,
∴ ∠BCE = ∠ACE + ∠ACB = 90°.
(2)①当点 D 在线段 BC 上时,如题图
(2).
∵ ∠DAE = ∠BAC,
∴ ∠BAC - ∠DAC = ∠DAE - ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE. 在△ABC 中,∠BAC + ∠B + ∠ACB = 180°,
∴ ∠BAC + ∠ACE + ∠ACB = 180°,
∴ ∠BAC + ∠BCE = 180°.
∵ ∠BAC = α,∠BCE = β,
∴ α + β = 180°.
②当点 D 在 BC 的延长线上时,如图
(1).
∵ ∠DAE = ∠BAC,
∴ ∠BAC + ∠DAC = ∠DAE + ∠DAC,
∴ ∠BAD = ∠CAE. 在△BAD 和△CAE 中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right.$
∴ △BAD≌△CAE(SAS),
∴ ∠B = ∠ACE. 在△ABC 中,∠BAC + ∠B + ∠ACB = 180°,
∴ ∠BAC + ∠ACE + ∠ACB = 180°,
∴ ∠BAC + ∠BCE = 180°.
∵ ∠BAC = α,∠BCE = β,
∴ α + β = 180°.
③当点 D 在 CB 的延长线上时,如图
(2). 同理可得△BAD≌△CAE,
∴ ∠ABD = ∠ACE. 在△ABC 中,∠BAC + ∠ABC + ∠ACB = 180°,
∴ ∠BAC + 180° - ∠ABD + ∠ACE - ∠BCE = 180°,
∴ ∠BAC = ∠BCE.
∵ ∠BAC = α,∠BCE = β,
∴ α = β. 综上所述,α 与 β 之间的数量关系为 α + β = 180°或 α = β.


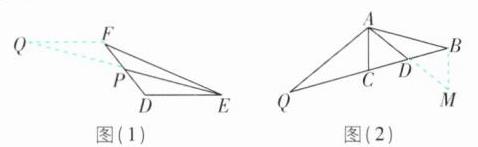
6 核心素养 几何直观 [2025 江苏南通期末,较难]
【探究与发现】
(1)如图(1),AD 是△ABC 的中线,延长 AD 至点 E,使 ED= AD,连接 BE,写出图中的全等三角形:____。(用“≌”连接)
【理解与应用】
(2)填空:如图(2),EP 是△DEF 的中线,若 EF= 5,DE= 3,设 EP= x,则 x 的取值范围是____。
(3)如图(3),AD 是△ABC 的中线,∠BAC= ∠ACB,点 Q 在 BC 的延长线上,QC= BC,求证:AQ= 2AD。
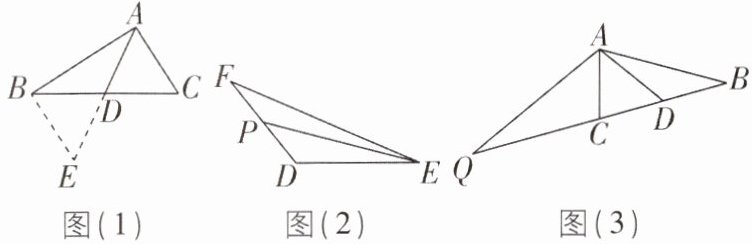
【探究与发现】
(1)如图(1),AD 是△ABC 的中线,延长 AD 至点 E,使 ED= AD,连接 BE,写出图中的全等三角形:____。(用“≌”连接)
【理解与应用】
(2)填空:如图(2),EP 是△DEF 的中线,若 EF= 5,DE= 3,设 EP= x,则 x 的取值范围是____。
(3)如图(3),AD 是△ABC 的中线,∠BAC= ∠ACB,点 Q 在 BC 的延长线上,QC= BC,求证:AQ= 2AD。

答案:
(1)【解】
∵ AD 是△ABC 的中线,
∴ CD = BD. 在△ADC 与△EDB 中,$\left\{\begin{array}{l} AD=DE,\\ ∠ADC=∠BDE,\\ CD=BD,\end{array}\right.$
∴ △ADC≌△EDB(SAS). 故答案为△ADC≌△EDB.
(2)【解】如图
(1),延长 EP 至点 Q,使 PQ = PE,连接 FQ.
∵ EP 是△DEF 的中线,
∴ PD = FP. 在△PDE 与△PQF 中,$\left\{\begin{array}{l} PE=PQ,\\ ∠EPD=∠QPF,\\ PD=PF,\end{array}\right.$
∴ △EDP≌△QFP(SAS),
∴ FQ = DE = 3. 在△EFQ 中,EF - FQ < QE < EF + FQ,即 5 - 3 < 2x < 5 + 3,
∴ x 的取值范围是 1 < x < 4. 故答案为 1 < x < 4.
(3)【证明】如图
(2),延长 AD 至 M,使 MD = AD,连接 BM,
∴ AM = 2AD.
∵ AD 是△ABC 的中线,
∴ BD = CD. 在△BMD 与△CAD 中,$\left\{\begin{array}{l} MD=AD,\\ ∠BDM=∠CDA,\\ BD=CD,\end{array}\right.$
∴ △BMD≌△CAD(SAS),
∴ BM = CA,∠M = ∠CAD,
∴ ∠BAC = ∠BAM + ∠CAD = ∠BAM + ∠M.
∵ ∠ACQ = 180° - ∠ACB,∠MBA = 180° - (∠BAM + ∠M) = 180° - ∠BAC,∠BAC = ∠ACB,
∴ ∠ACQ = ∠MBA.
∵ QC = BC,
∴ QC = AB. 在△ACQ 与△MBA 中,$\left\{\begin{array}{l} CA=BM,\\ ∠ACQ=∠MBA,\\ QC=AB,\end{array}\right.$
∴ △ACQ≌△MBA(SAS),
∴ AQ = AM = 2AD.
(1)【解】
∵ AD 是△ABC 的中线,
∴ CD = BD. 在△ADC 与△EDB 中,$\left\{\begin{array}{l} AD=DE,\\ ∠ADC=∠BDE,\\ CD=BD,\end{array}\right.$
∴ △ADC≌△EDB(SAS). 故答案为△ADC≌△EDB.
(2)【解】如图
(1),延长 EP 至点 Q,使 PQ = PE,连接 FQ.
∵ EP 是△DEF 的中线,
∴ PD = FP. 在△PDE 与△PQF 中,$\left\{\begin{array}{l} PE=PQ,\\ ∠EPD=∠QPF,\\ PD=PF,\end{array}\right.$
∴ △EDP≌△QFP(SAS),
∴ FQ = DE = 3. 在△EFQ 中,EF - FQ < QE < EF + FQ,即 5 - 3 < 2x < 5 + 3,
∴ x 的取值范围是 1 < x < 4. 故答案为 1 < x < 4.
(3)【证明】如图
(2),延长 AD 至 M,使 MD = AD,连接 BM,
∴ AM = 2AD.
∵ AD 是△ABC 的中线,
∴ BD = CD. 在△BMD 与△CAD 中,$\left\{\begin{array}{l} MD=AD,\\ ∠BDM=∠CDA,\\ BD=CD,\end{array}\right.$
∴ △BMD≌△CAD(SAS),
∴ BM = CA,∠M = ∠CAD,
∴ ∠BAC = ∠BAM + ∠CAD = ∠BAM + ∠M.
∵ ∠ACQ = 180° - ∠ACB,∠MBA = 180° - (∠BAM + ∠M) = 180° - ∠BAC,∠BAC = ∠ACB,
∴ ∠ACQ = ∠MBA.
∵ QC = BC,
∴ QC = AB. 在△ACQ 与△MBA 中,$\left\{\begin{array}{l} CA=BM,\\ ∠ACQ=∠MBA,\\ QC=AB,\end{array}\right.$
∴ △ACQ≌△MBA(SAS),
∴ AQ = AM = 2AD.

查看更多完整答案,请扫码查看


