《2025年初中必刷题八年级数学上册苏科版》

2024年国庆假期期间,苏州文旅市场持续七天“人从众”模式,不断升温的消费热情,让网友直呼:“这来了得有一亿人.”据当地通信运营商数据,2024年国庆假期,苏州全市累计接待游客约$1.29×10^7$人次.其中$1.29×10^7$精确到 (A)
A.十万位
B.百万位
C.十分位
D.百分位

答案： @@1. A [解析]1.29×10⁷=12900000,
∴近似值@@1.29×10⁷精确到十万位. 故选 A.
 

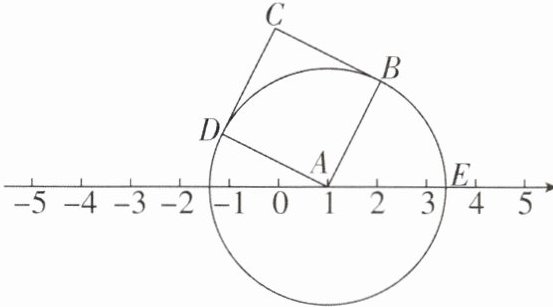
2 [2025江苏镇江质检]如图,已知正方形ABCD的面积为5,点A在数轴上,且表示的数为1.现以点A为圆心,以AB的长为半径作圆,所得圆和数轴交于点E(E在A的右侧),则点E表示的数为 ( )

A.$\sqrt{5}+1$
B.3.2
C.$\sqrt{5}-1$
D.$\sqrt{13}$

答案： 2. A [解析]
∵正方形 ABCD 的面积为 5,且 AB=AE,
∴AB=AE=$\sqrt{5}$.
∵点 A 表示的数是 1,且点 E 在点 A 的右侧,
∴点 E 表示的数为 $\sqrt{5}$+1. 故选 A.

3 若$3(x + y - 4)^2与5\sqrt{2x - y + 1}$互为相反数,则$10x + 2y$的平方根是 (B)
A.16
B.±4
C.±2
D.4

答案： B [解析]由题意得 3(x+y - 4)²+5$\sqrt{2x - y + 1}$=0,
∴$\begin{cases}x + y - 4 = 0\\2x - y + 1 = 0\end{cases}$,
∴$\begin{cases}x = 1\\y = 3\end{cases}$,
∴10x+2y=16,而 16 的平方根为±4,
∴10x+2y 的平方根是±4. 故选 B.

4 设$S_1= 1+\frac{1}{1^2}+\frac{1}{2^2}$,$S_2= 1+\frac{1}{2^2}+\frac{1}{3^2}$,$S_3= 1+\frac{1}{3^2}+\frac{1}{4^2}$,…,$S_n= 1+\frac{1}{n^2}+\frac{1}{(n + 1)^2}$,则$\sqrt{S_1}+\sqrt{S_2}+…+\sqrt{S_{24}}$的值为 (A)
A.$\frac{624}{25}$
B.$\frac{\sqrt{24}}{5}$
C.$\frac{24}{25}$
D.$\frac{575}{24}$

答案： A [解析]$\sqrt{S₁}$=$\sqrt{1 + 1 + \frac{1}{4}}$=$\frac{3}{2}$,$\sqrt{S₂}$=$\sqrt{1 + \frac{1}{4} + \frac{1}{9}}$=$\frac{7}{6}$,$\sqrt{S₃}$=$\sqrt{1 + \frac{1}{9} + \frac{1}{16}}$=$\frac{13}{12}$,$\sqrt{S₄}$=$\sqrt{1 + \frac{1}{16} + \frac{1}{25}}$=$\frac{21}{20}$,…,$\sqrt{Sₙ}$=1 + $\frac{1}{n}$ - $\frac{1}{n + 1}$,
∴$\sqrt{S₁}$+$\sqrt{S₂}$+…+$\sqrt{S₂₄}$=1 + 1 - $\frac{1}{2}$+1 + $\frac{1}{2}$ - $\frac{1}{3}$+…+1 + $\frac{1}{24}$ - $\frac{1}{25}$=24 + 1 - $\frac{1}{25}$=$\frac{624}{25}$. 故选 A.

5 计算$\sqrt{81}+|2-\sqrt{3}|+\sqrt[3]{-125}+6÷(-\frac{3}{4})= $______.

答案： @@5. -2 - $\sqrt{3}$ [解析]原式=9+2 - $\sqrt{3}$ - 5 - 8=-2 - $\sqrt{3}$. 故答案为 -2 - $\sqrt{3}$.
 

6 已知a,b都是实数,$b= \sqrt{1 - 2a}+\sqrt{4a - 2}-2$,则$a^b$的值为______.

答案： 6. 4 [解析]根据题意得$\begin{cases}1 - 2a\geq0\\4a - 2\geq0\end{cases}$,解得 a=$\frac{1}{2}$.当 a=$\frac{1}{2}$时,b=-2,所以 aᵇ=($\frac{1}{2}$)⁻²=4. 故答案为@@4.

在实数$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$,…,$\sqrt{2022}$,$\sqrt{2023}$,$\sqrt{2024}$中,无理数有1980个.

答案： 1980 [解析]
∵44²=1936,45²=2025,
∴44＜$\sqrt{2024}$＜45,
∴在实数$\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$,$\sqrt{4}$,…,$\sqrt{2022}$,$\sqrt{2023}$,$\sqrt{2024}$中,有理数有 44 个,
∴无理数有 2024 - 44=1980(个),故答案为 1980.

8 [2025江苏徐州期中]通过下列方法可将$x= \frac{\sqrt{5}-1}{2}转化为方程x^2 + x - 1 = 0$,我们规定:方程$x^2 + x - 1 = 0为x= \frac{\sqrt{5}-1}{2}$的还原方程.
$x= \frac{\sqrt{5}-1}{2}$,去分母,得$2x= \sqrt{5}-1$,
移项,得$2x + 1= \sqrt{5}$,
两边平方,得$4x^2 + 4x + 1 = 5$,
整理,得$x^2 + x - 1 = 0$.
则$x= \frac{\sqrt{5}+3}{2}$的还原方程是x² - 3x + 1=0.

答案： x² - 3x + 1=0 [解析]x=$\frac{\sqrt{5} + 3}{2}$,去分母,得 2x=$\sqrt{5}$+3,移项,得 2x - 3=$\sqrt{5}$,两边平方,得 4x² - 12x + 9=5,整理,得 x² - 3x + 1=0,故答案为 x² - 3x + 1=0.

9 已知$x - 6和3x + 14$分别是a的两个平方根,$2y + 2$是a的立方根.
(1)求a,x,y的值.
(2)求$1 - 4x$的平方根和算术平方根.

答案： 【解】
(1)由题意得 x - 6+3x + 14=0,解得 x=-2,
∴a=(x - 6)²=64. 又
∵2y + 2 是 a 的立方根,
∴2y + 2=$\sqrt[3]{64}$=4,
∴y=1.综上,a=64,x=-2,y=1.
(2)
∵1 - 4x=9,
∴1 - 4x 的平方根为±3,算术平方根为 3.

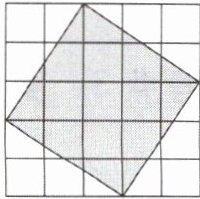
10 如图,已知每个小正方形的边长为1.
(1)图中阴影正方形的面积是______,边长是______,在数轴上准确地作出表示阴影正方形边长的点.

(2)已知x为阴影正方形边长的小数部分,y为$\sqrt{15}$的整数部分.
求:①x,y的值.②$(x + y)^2$的算术平方根.

答案：
【解】
(1)阴影正方形的面积为 5×5 - 4×$\frac{1}{2}$×3×2=13,边长为 $\sqrt{13}$,故答案为 13, $\sqrt{13}$.作出表示阴影正方形边长的点 A 如图所示.

(2)①
∵9＜13＜16,9＜15＜16,
∴3＜$\sqrt{13}$＜4,3＜$\sqrt{15}$＜4.
∵x 为阴影正方形边长的小数部分,y 为$\sqrt{15}$的整数部分,
∴x=$\sqrt{13}$ - 3,y=3.②由①得 x=$\sqrt{13}$ - 3,y=3,
∴(x + y)²=($\sqrt{13}$ - 3+3)²=13,
∴(x + y)² 的算术平方根是$\sqrt{13}$.