《2025年初中必刷题八年级数学上册苏科版》

1 [2024 江苏连云港期中]如图,AC,BD 相交于点 O,若 OA= OD,用“ASA”证明△AOB≌△DOC,还需添加条件(B)

A.∠AOB= ∠DOC
B.∠BAC= ∠BDC
C.∠BCD= ∠ADC
D.AB= CD

答案： B 【解析】还需添加∠BAC=∠BDC.
∵∠BAC=∠BDC,OA=OD,∠AOB=∠DOC,
∴△AOB≌△DOC(ASA),故选B.

2 新考向 开放性试题 如图,AB//CD,AD 与 BC 交于点 O,请添加一个条件：AB=DC,使△AOB≌△DOC.(只填一种情况即可)

答案： AB=DC(答案不唯一) 【解析】
∵AB//CD,
∴∠A=∠D,∠B=∠C,
∴添加AB=DC,由ASA即可证明△AOB≌△DOC. 故答案为AB=DC(答案不唯一).

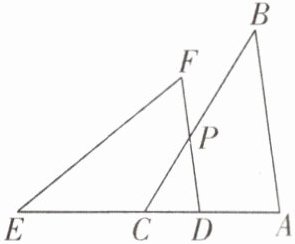
3 [2025 江苏宿迁质检]如图,点 E,C,D,A 在同一条直线上,AB//DF,ED= AB,∠E= ∠CPD,求证：△ABC≌△DEF.

答案： 【证明】
∵AB//DF,
∴∠B=∠CPD,∠A=∠FDE.
∵∠E=∠CPD,
∴∠E=∠B.在△ABC和△DEF中,∠B=∠E,AB=ED,∠A=∠FDE,
∴△ABC≌△DEF(ASA).

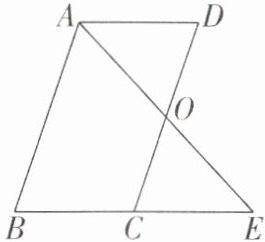
4 [2025 江苏连云港质检]如图,AB//CD,∠B= ∠D,O 是 CD 的中点,连接 AO 并延长,交 BC 的延长线于点 E.
(1)试判断 AD 与 BE 的位置关系,并说明理由；
(2)试说明△AOD≌△EOC.

答案： 【解】
(1)AD//BE. 理由:
∵AB//CD,
∴∠B=∠DCE.
∵∠B=∠D,
∴∠DCE=∠D,
∴AD//BE.
(2)
∵O是CD的中点,
∴DO=CO.在△ADO和△ECO中,∠D=∠OCE,DO=CO,∠AOD=∠COE,
∴△AOD≌△EOC(ASA).

5 [2024 江苏南京浦口区质检]如图是嘉淇测量水池 AB 宽度的方案,下列说法不正确的是(D)
①过点 B 作 BF⊥AB；②在 BF 上取 C,D 两点,使得△BC=CD；③过点 D 作 DE⊥BF；④作射线AC,交 DE 于点 M；⑤测量DM的长度,即为水池 AB 的宽度.

A.△代表 BC= CD
B.□代表 AC
C.☆代表 DM
D.该方案的依据是 SAS

答案： D 【解析】完整步骤为①过点B作BF⊥AB;②在BF上取C,D两点,使得BC=CD;③过点D作DE⊥BF;④作射线AC,交DE于点M;⑤测量DM的长度，即为水池AB的宽度.
∵BF⊥AB,DE⊥BF,
∴∠ABC=∠MDC=90°.
∵BC=CD,∠ACB=∠MCD,
∴△ABC≌△MDC(ASA),
∴AB=DM,
∴该方案的依据是ASA,
∴选项D错误.故选D.

6 小明不慎将一块三角形玻璃打碎成如图所示的四块(图中所标 1,2,3,4),你认为将其中的4带去商店,就能配一块与原来完全一样的三角形玻璃.

答案： 4 【解析】由题图可知，应该带4去商店，符合“角边角”，可以配一块与原来完全一样的三角形玻璃.

7 [2025 江苏宿迁质检]如图,在△ABC 中,高 AD,CE 交于点 H. 若 AB= 19,CE= AE= 12,则 CH= ______.


5

答案： 5 【解析】
∵高AD,CE交于点H,
∴∠BCE+∠CHD=90°,∠EAH+∠AHE=90°.又
∵∠AHE=∠CHD,
∴∠BCE=∠EAH.在△BCE和△HAE中,∠BCE=∠HAE,CE=AE,∠CEB=∠AEH=90°,
∴△BCE≌△HAE(ASA),
∴BE=EH.
∵BE+AE=AB=19,CE=AE=12,
∴BE=EH=7,
∴CH=CE - HE=12 - 7=5,故答案为5.

8 [2025 江苏镇江调研]如图,四边形 ABCD 中,对角线 AC,BD 交于点 O,AB= AC,点 E 是 BD 上一点,且∠ABD= ∠ACD,∠EAD= ∠BAC.
(1)求证：AE= AD；
(2)若∠BAC= 50°,求∠BDC 的度数.

答案：
(1)【证明】
∵∠BAC=∠EAD,
∴∠BAC - ∠EAC=∠EAD - ∠EAC,
∴∠BAE=∠CAD.在△ABE和△ACD中,∠ABD=∠ACD,AB=AC,∠BAE=∠CAD,
∴△ABE≌△ACD(ASA),
∴AE=AD.
(2)【解】
∵∠ABD=∠ACD,∠AOB=∠COD,∠BAC+∠ABD+∠AOB=∠COD+∠ACD+∠BDC=180°,
∴∠BDC=∠BAC=50°.