《2025年初中必刷题八年级数学上册苏科版》

1在$Rt△ABC$中,$∠A,∠B,∠C$的对边分别是a,b,c,若$∠B+∠C= 90^{\circ }$,则下列等式中成立的是(B)
A.$a^{2}+b^{2}= c^{2}$
B.$b^{2}+c^{2}= a^{2}$
C.$a^{2}+c^{2}= b^{2}$
D.$b+c= a$

答案： B　[解析]
∵∠B+∠C=90°,
∴∠A=90°,
∴b²+c²=a².故选B.

如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,6,3,则正方形D的面积为(C)
A.6
B.8
C.11
D.12

答案： C　[解析]设正方形A,B,C,D的边长分别为a,b,c,d,中间阴影正方形的边长为x.
∵两个三角形为直角三角形，
∴a²+b²=x²,x²+c²=d²,
∴d²=a²+b²+c².
∵A,B,C三个正方形的面积分别为2,6,3,
∴d²=a²+b²+c²=2+6+3=11,
∴正方形D的面积为11.故选C.

3若一个直角三角形的两边长分别为4和5,则第三条边长为3或$\sqrt{41}$.

答案： 3或$\sqrt{41}$　[解析]当5为直角边长时，第三条边长的平方为4²+5²=41;当5为斜边长时,第三条边长的平方为5²−4²=9,故第三条边长为3或$\sqrt{41}$.故答案为3或$\sqrt{41}$

在$Rt△ABC$中,$∠C= 90^{\circ },∠A,∠B,∠C$的对边分别为a,b,c.若$a:b= 3:4,c= 20cm$,则$b= $16cm.

答案： 16cm　[解析]
∵a:b=3:4,
∴设a=3xcm,b=4xcm.
∵c=20cm,
∴由勾股定理可得(3x)²+(4x)²=20²,解得x=4(负值已舍去),
∴b=4×4=16(cm).故答案为16cm.

如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 3,AB= 5,AB$的垂直平分线交BC于点D,连接AD,则$△ACD$的周长是(A)
A.7
B.8
C.9
D.10

答案： A　[解析]
∵∠C=90°,AC=3,AB=5,
∴BC²=AB²−AC²=16,
∴BC=4.
∵AB的垂直平分线交BC于点D,
∴AD=BD,
∴△ACD的周长为AC+AD+CD=AC+CD+BD=AC+BC=4+3=7.故选A.

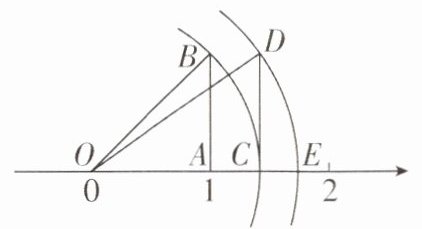
6[2025山西临汾期末]如图所示,点O为数轴的原点,点A在数轴上表示1,作腰长为1的等腰直角三角形OAB,其中$∠OAB= 90^{\circ }$,以点O为圆心,OB长为半径作弧,交数轴于点C,作直角三角形OCD,其中$∠OCD= 90^{\circ },CD= 1$,以点O为圆心,OD长为半径作弧,交数轴于点E,则点E表示的实数为$\sqrt{3}$.

答案： $\sqrt{3}$　[解析]
∵在等腰直角三角形OAB中，∠OAB=90°,OA=1,
∴OC=OB=$\sqrt{1²+1²}$=$\sqrt{2}$.
∵∠OCD=90°,CD=1,
∴OE=OD=$\sqrt{(\sqrt{2})²+1²}$=$\sqrt{3}$,
∴点E表示的实数为$\sqrt{3}$.故答案为$\sqrt{3}$

7[2025江苏南京期中]在$△ABC$中,$∠BAC和∠ABC$都是锐角,$BC= a,AC= b,AB= c$.如图(1),当$∠ACB= 90^{\circ }$时,$a^{2}+b^{2}= c^{2}$.
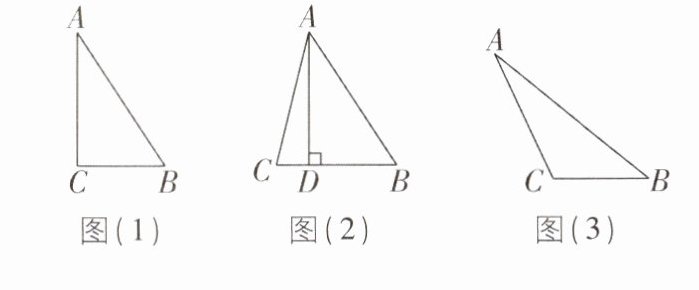
(1)如图(2),当$∠ACB＜90^{\circ }$时,小明猜想$a^{2}+b^{2}＞c^{2}$,理由如下:
过点A作$AD⊥BC$,垂足为D,设$CD= x$,…完成小明的证明过程.
(2)如图(3),当$∠ACB＞90^{\circ }$时,猜想$a^{2}+b^{2}与c^{2}$的大小关系,并证明你的猜想.

答案： [解]
(1)
∵AD²=b²−x²,AD²=c²−(a−x)²,则b²−x²=c²−(a−x)²,
∴a²+b²=c²+2ax.
∵a＞0,x＞0,
∴2ax＞0,
∴a²+b²＞c²,
∴当∠ACB＜90°时,a²+b²＞c².
(2)当∠ACB＞90°时,a²+b²与c²的大小关系为a²+b²＜c².证明:如图,过点A作AD⊥BC,交BC的延长线于点D,设CD=x.
本题因为没有图形，所以在解题时画出符合条件的图形就显得尤为重要，应按∠ACB为锐角或钝角两种情况分类讨论
根据勾股定理得到AC²+BC²=AB²,再结合三角形及圆的面积公式和完全平方公式求解.
∵AD²=AC²−DC²=b²−x²,AD²=AB²−BD²=c²−(a+x)²,
∴b²−x²=c²−(a+x)²,
∴a²+b²=c²−2ax.
∵a＞0,x＞0,
∴2ax＞0,
∴a²+b²=c²−2ax＜c²,
∴当∠ACB＞90°时,a²+b²＜c².

8在$△ABC$中,$AB= 20,AC= 15,BC$边上的高AD为12,则BC的长为____.

答案：
25或7　[解析]分两种情况讨论:如图
(1),当∠ACB为锐角时,在Rt△ABD中,BD²=AB²−AD²=20²−12²=256,
∴BD=16.在Rt△ACD中,CD²=AC²−AD²=15²−12²=81,
∴CD=9,
∴BC=BD+CD=25.
如图
(2),当∠ACB为钝角时,在Rt△ABD中,BD²=AB²−AD²=20²−12²=256,
∴BD=16.在Rt△ACD中,CD²=AC²−AD²=15²−12²=81,
∴CD=9,
∴BC=BD−CD=7. 综上所述,BC的长为25或7.