《2025年初中必刷题八年级数学上册苏科版》

1 [2024江苏镇江期中]若△ABC的三边分别是a,b,c,则下列条件能判断△ABC是直角三角形的是(D)
A.∠A= ∠B= 2∠C
B.∠A:∠B:∠C= 3:4:5
C.a= 4,b= 5,c= 6

$D.a = m^2 - n^2,b = 2mn,c = m^2 + n^2(m ＞ n ＞ 0)$

答案： D【解析】
∵∠A = ∠B = 2∠C，且∠A + ∠B + ∠C = 180°，
∴∠A = ∠B = 72°，∠C = 36°，
∴△ABC不是直角三角形，选项A不符合题意.
∵∠A:∠B:∠C = 3:4:5，
∴∠C为最大角，且∠C = $\frac{5}{3 + 4 + 5}$×180° = 75°，
∴△ABC不是直角三角形，选项B不符合题意.
∵a = 4，b = 5，c = 6，
∴a² + b² ≠ c²，
∴△ABC不是直角三角形，选项C不符合题意.
∵a = m² - n²，b = 2mn，c = m² + n²(m ＞ n ＞ 0)，
∴c² - a² = (m² + n²)² - (m² - n²)² = (m² + n² + m² - n²)(m² + n² - m² + n²) = 4m²n² = (2mn)² = b²，即a² + b² = c²，
∴△ABC是直角三角形，选项D符合题意.故选D.

如果正整数a,b,c满足等式$a^2 + b^2 = c^2,$那么正整数a,b,c叫作勾股数,某同学将自己探究勾股数的过程列成右表,观察表中每列数的规律,可知x + y的值为(C)
A.47
B.62
C.79
D.98

答案： C【解析】由题可得，3 = 2² - 1，4 = 2×2，5 = 2² + 1；8 = 3² - 1，6 = 2×3，10 = 3² + 1；……，
∴a = n² - 1，b = 2n，c = n² + 1，
∴当c = n² + 1 = 65时，n² = 65 - 1 = 64 = 8²，
∴n = 8，
∴x = 63，y = 16，
∴x + y = 79.故选C.

3 如图,三角形纸片ABC中,∠BAC= 90°,AB= 2,AC= 3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处；再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是(A)
A.$\frac{13}{6}$
B.$\frac{5}{6}$
C.$\frac{7}{6}$
D.$\frac{6}{5}$

答案： A【解析】由折叠的性质可知，AD = AB = 2，∠B = ∠ADB，CE = DE，∠C = ∠CDE.
∵∠BAC = 90°，
∴∠B + ∠C = 90°，
∴∠ADB + ∠CDE = 90°，
∴∠ADE = 90°，
∴AD² + DE² = AE².设AE = x，则CE = DE = 3 - x，
∴2² + (3 - x)² = x²，解得x = $\frac{13}{6}$，
∴AE = $\frac{13}{6}$.故选A.

4 如图,点D在△ABC的边BC上,点E是AC的中点,若AB= 13,AD= 12,BD= 5,DE= 10,则CD的长为(D)
A.13
B.14
C.15
D.16

答案： D【解析】
∵AB = 13，AD = 12，BD = 5，
∴BD² + AD² = AB²，
∴△ABD为直角三角形，∠ADB = 90°，
∴AD⊥BC.在Rt△ADC中，点E是斜边AC的中点，且DE = 10，
∴AC = 20，由勾股定理，得CD² = AC² - AD² = 20² - 12² = 256 = 16²，
∴CD = 16.故选D.

5 [2025江苏连云港期末]如图,∠MON= 90°,已知△ABC中,AC= BC= 10,AB= 12,△ABC的顶点A,B分别在边OM,ON上,当点B在边ON上运动时,点A随之在边OM上运动,△ABC的形状保持不变,在运动过程中,点C到点O的最
大距离为( )


A.12.5
B.13
C.14
D.15

答案：
C【解析】取AB的中点D，连接CD，如图所示.
∵AC = BC = 10，AB = 12，点D是AB边中点，
∴BD = $\frac{1}{2}$AB = 6，CD⊥AB，
∴CD = $\sqrt{BC² - BD²}$ = $\sqrt{10² - 6²}$ = 8.连接OD，OC，则OC ≤ OD + DC，
∴当O，D，C三点共线时，OC有最大值，最大值是OD + CD.又
∵△AOB为直角三角形，D为斜边AB的中点，
∴OD = $\frac{1}{2}$AB = 6，
∴OD + CD = 6 + 8 = 14，即点C到点O的最大距离为14，故选C.

6 [2024浙江舟山期末]如图,在Rt△ABC和Rt△BDE中,∠ABC= ∠BDE= 90°,点A是边DE的中点,若AB= BC,DB= DE= 2,连接CE,则$CE^2$的值为( )


A.14
B.15
C.16
D.17

答案：
D【解析】延长ED到F，使得DF = DE，连接CF，BF，如图所示.
∵BD = DE = 2，∠BDE = 90°，
∴∠BDE = ∠BDF = 90°，EF = 4.又
∵BD = BD，
∴△BDE≌△BDF(SAS)，
∴BE = BF，∠BEA = ∠BFA = ∠EBD = ∠FBD = 45°，
∴∠EBF = 90°.
∵∠EBA + ∠ABF = 90°，∠ABF + ∠FBC = 90°，
∴∠EBA = ∠FBC.
∵BE = BF，BA = BC，
∴△EBA≌△FBC(SAS)，
∴∠BEA = ∠BFC = 45°，AE = CF，
∴∠CFE = ∠BFC + ∠AFB = 90°.
∵点A为DE的中点，
∴AE = 1，
关键点拨：本题考查了折叠问题、勾股定理以及三角形面积的计算，熟练掌握折叠的性质是解题的关键.
思路分析：延长ED到F，使得DF = DE，连接CF，BF，然后根据全等三角形的判定和性质以及勾股定理，即可求得CE²的值.
∴CF = 1，
∴EC² = EF² + CF² = 4² + 1² = 17.故选D.

7 [2025安徽阜阳期中]如图,四边形ABCD的对角线AC⊥BD,相交于点O.若AB= 3CD= 6,则$AD^2 + BC^2 = $40.

答案： 40【解析】
∵AB = 3CD = 6，
∴CD = 2.
∵AC⊥BD，
∴AD² + BC² = (AO² + DO²) + (BO² + CO²) = (AO² + BO²) + (DO² + CO²) = AB² + CD² = 6² + 2² = 40.故答案为40.

8 [2024吉林长春调研]如图是由小正方形组成的网格,点A,B,C,D,E是网格线的交点,则∠DAE - ∠BAC的度数为____°.

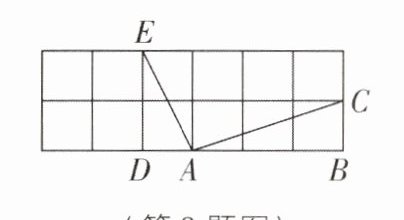
答案：
45【解析】连接AF，EF，如图所示.由图易得△AFG≌△ACB，
∴∠BAC = ∠GAF，
∴∠DAE - ∠BAC = ∠DAE - ∠GAF = ∠FAE.设每个小正方形的边长为a，则AE² = EF² = a² + (2a)² = 5a²，AF² = a² + (3a)² = 10a²，
∴AE = EF，AE² + EF² = AF²，
∴△AEF是等腰直角三角形，
∴∠FAE = 45°，
∴∠DAE - ∠BAC = 45°.故答案为45.

9 [2024江苏江阴期中]如图,将△ABC沿AC翻折得到△ADC,BD交AC于点E,F为CD中点,连接AF并延长交BC的延长线于点G,连接EF,若AB= 15,AE= 9,△ADF的面积为42,则△DEF的面积为____15.

答案： 15【解析】
∵将△ABC沿AC翻折得到△ADC，
∴AC⊥BD，BE = DE.
∵AB = 15，AE = 9，
∴BE² = DE² = AB² - AE² = 12²，
∴BE = DE = 12.
∵△ADF的面积为42，F为CD中点，
$∴S_{△ACD} = 2S_{△ADF} = 2×42 = 84，$
∴$\frac{1}{2}$AC·DE = 84，
∴AC = 14，
∴CE = AC - AE = 5，
$∴S_{△CDE} = 2S_{△DEF} = \frac{1}{2}CE·DE = \frac{1}{2}×5×12 = 30，$
∴△DEF的面积为15.故答案为15.

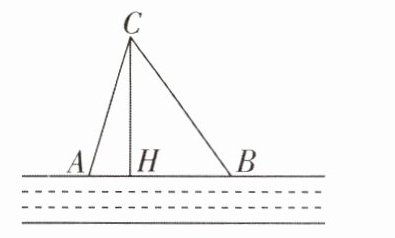
10 [2024江苏盐城质检]如图,笔直的河流一侧有一营地C,河边有两个漂流点A,B,其中AB= AC,由于周边施工,由C到A的路AC现在已经不通,为方便游客通行,在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC= 10千米,CH= 8千米,BH= 6千米,则原路AC的长为$8\frac{1}{3}$千米.

答案： $8\frac{1}{3}$【解析】
∵BC = 10千米，CH = 8千米，BH = 6千米，
∴CH² + BH² = 8² + 6² = 100，BC² = 100，
∴CH² + BH² = BC²，
∴△HBC是直角三角形且∠CHB = 90°.设AC = AB = x千米，则AH = AB - BH = (x - 6)千米.在Rt△ACH中，由勾股定理得AC² = AH² + CH²，
∴x² = (x - 6)² + 8²，解得x = $8\frac{1}{3}$，故答案为$8\frac{1}{3}$.