《2025年初中必刷题八年级数学上册苏科版》

我国是最早了解勾股定理的国家之一,《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现的,故又称之为商高定理.下列四幅图中(每个图中的阴影三角形均为全等的直角三角形),不能证明勾股定理的是(C)

答案： C 【解析】A 选项,梯形的面积为$\frac {1}{2}(a+b)(a+b)=\frac {1}{2}(a^{2}+b^{2})+ab$,该梯形也可看作是由2个直角三角形和一个等腰直角三角形组成的,则其面积为$\frac {1}{2}ab×2+\frac {1}{2}c^{2}=ab+\frac {1}{2}c^{2},\therefore ab+\frac {1}{2}c^{2}=\frac {1}{2}(a^{2}+b^{2})+ab,\therefore a^{2}+b^{2}=c^{2}$,故A 选项能证明勾股定理;B 选项,大正方形的面积为$c^{2}$,该大正方形也可看作是由4个直角三角形和一个小正方形组成的,则其面积为$\frac {1}{2}ab×4+(b-a)^{2}=a^{2}+b^{2},\therefore a^{2}+b^{2}=c^{2}$,故 B 选项能证明勾股定理;C 选项,大正方形的面积为$(a+b)^{2}$,该大正方形也可看作是由2个长方形和2个小正方形组成的,则其面积为$a^{2}+b^{2}+2ab,\therefore (a+b)^{2}=a^{2}+b^{2}+2ab$,
∴ C 选项不能证明勾股定理;D 选项,大正方形的面积为$(a+b)^{2}$,该大正方形也可看作是由4个直角三角形和一个小正方形组成的,则其面积为$\frac {1}{2}ab×4+c^{2}=2ab+c^{2},\therefore (a+b)^{2}=2ab+c^{2},\therefore a^{2}+b^{2}=c^{2}$,故 D 选项能证明勾股定理. 故选 C.

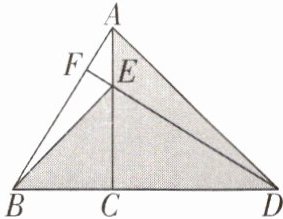
2[2024江苏南京期末]如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连接BE,DE,DE的延长线交AB于F,已知DE= AB,∠CAD= 45°.
(1)求证：DF⊥AB；
(2)利用图中阴影部分面积完成勾股定理的证明：已知：如图,在△ABC中,∠ACB= 90°,BC= a,AC= b,AB= c,求证：$a^{2}+b^{2}= c^{2}$.

答案： 【证明】
(1)$\because AC⊥BD,∠CAD=45^{\circ },\therefore AC=DC,∠ACB=∠DCE=90^{\circ }$. 在$Rt△ABC$与$Rt△DEC$中,$\left\{\begin{array}{l} AC=DC,\\ AB=DE,\end{array}\right. \therefore Rt△ABC\cong Rt△DEC(HL),\therefore ∠BAC=∠EDC.\because ∠EDC+∠CED=90^{\circ },∠CED=∠AEF,\therefore ∠AEF+∠BAC=90^{\circ },\therefore ∠AFE=90^{\circ },\therefore DF⊥AB.$
(2)$\because △ABC\cong △DEC,\therefore BC=CE.\because S_{△BCE}+S_{△ACD}=S_{△ABD}-S_{△ABE},\therefore \frac {1}{2}a^{2}+\frac {1}{2}b^{2}=\frac {1}{2}\cdot c\cdot DF-\frac {1}{2}\cdot c\cdot EF=\frac {1}{2}\cdot c\cdot (DF-EF)=\frac {1}{2}\cdot c\cdot DE=\frac {1}{2}c^{2},\therefore a^{2}+b^{2}=c^{2}.$

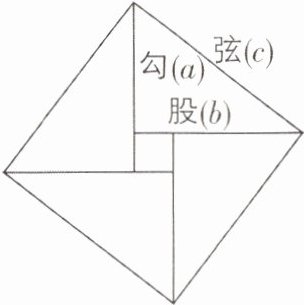
3新考向传统文化[2023江苏扬州中考]我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a,b,斜边长为c,若b-a= 4,c= 20,则每个直角三角形的面积为______.

96

答案： 96 【解析】由题图可得,$a^{2}+b^{2}=c^{2},\therefore a^{2}+b^{2}=20^{2},\therefore (b-a)^{2}+2ab=400,\therefore 4^{2}+2ab=400,\therefore ab=192$,
∴ 每个直角三角形的面积为$\frac {1}{2}ab=\frac {1}{2}×192=96$,故答案为 96.

(1)填空：用古人的方法计算$DF^{2}$的值如下：
$DF^{2}= DE^{2}-EF^{2}= BH^{2}-CH^{2}= ($AB$^{2}-$AH$^{2})-($AC$^{2}-$AH$^{2})= $16；
(2)试直接利用阅读材料中勾股定理的推论继续完成△ABC面积的计算过程；
在$Rt△DEF$中,由勾股定理的推论$a=\frac {(c+a)^{2}-b^{2}}{2(c+a)}$,可得$EF=\frac {(DE+EF)^{2}-DF^{2}}{2(DE+EF)}.\because DE+EF=BH+CH=BC=8,DF^{2}=16,\therefore EF=\frac {8^{2}-16}{2×8}=\frac {64-16}{16}=3,\therefore CH=3$. 在$Rt△ACH$中,$AH^{2}=AC^{2}-CH^{2}=5^{2}-3^{2}=16,\therefore AH=4,\therefore S_{△ABC}=\frac {1}{2}\cdot BC\cdot AH=16.$
(3)你还有其他计算△ABC的面积的方法吗？写出解答过程.
设$CH=x$,则$BH=8-x.$由勾股定理,得$AH^{2}=AB^{2}-BH^{2}=AC^{2}-CH^{2},\therefore (\sqrt {41})^{2}-(8-x)^{2}=5^{2}-x^{2}$,解得$x=3,\therefore CH=3,\therefore AH=\sqrt {5^{2}-3^{2}}=4,\therefore S_{△ABC}=\frac {1}{2}BC\cdot AH=\frac {1}{2}×8×4=16.$

答案： 【解】
(1)$DF^{2}=DE^{2}-EF^{2}=BH^{2}-CH^{2}=(AB^{2}-AH^{2})-(AC^{2}-AH^{2})=16$,故答案为 AB,AH,AC,AH,16.
(2)在$Rt△DEF$中,由勾股定理的推论$a=\frac {(c+a)^{2}-b^{2}}{2(c+a)}$,可得$EF=\frac {(DE+EF)^{2}-DF^{2}}{2(DE+EF)}.\because DE+EF=BH+CH=BC=8,DF^{2}=16,\therefore EF=\frac {8^{2}-16}{2×8}=\frac {64-16}{16}=3,\therefore CH=3$. 在$Rt△ACH$中,$AH^{2}=AC^{2}-CH^{2}=5^{2}-3^{2}=16,\therefore AH=4,\therefore S_{△ABC}=\frac {1}{2}\cdot BC\cdot AH=16.$
(3)如题图
(2),设$CH=x$,则$BH=8-x.$由勾股定理,得$AH^{2}=AB^{2}-BH^{2}=AC^{2}-CH^{2},\therefore (\sqrt {41})^{2}-(8-x)^{2}=5^{2}-x^{2}$,解得$x=3,\therefore CH=3,\therefore AH=\sqrt {5^{2}-3^{2}}=4,\therefore S_{△ABC}=\frac {1}{2}BC\cdot AH=\frac {1}{2}×8×4=16.$