第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [中]如图,已知$AB⊥CD$,$AB= CD$,$E$,$F是AD$上的两个点,$CE⊥AD$,$BF⊥AD$。若$AD= a$,$BF= b$,$CE= c$,则$EF$的长为(
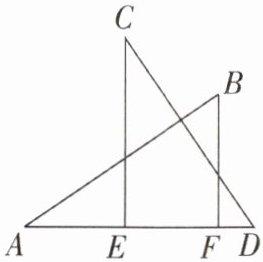
A.$a+b-c$
B.$b+c-a$
C.$a+c-b$
D.$a-b$
B
)
A.$a+b-c$
B.$b+c-a$
C.$a+c-b$
D.$a-b$
答案:
B 【解析】
∵ AB⊥CD,CE⊥AD,
∴ ∠C + ∠D = 90°,∠A + ∠D = 90°,
∴ ∠A = ∠C. 又
∵ AB = CD,∠AFB = ∠CED = 90°,
∴ △ABF≌△CDE(AAS),
∴ BF = DE = b,CE = AF = c.
∵ AE = AD - DE = a - b,
∴ EF = AF - AE = c - (a - b) = c - a + b. 故选 B.
∵ AB⊥CD,CE⊥AD,
∴ ∠C + ∠D = 90°,∠A + ∠D = 90°,
∴ ∠A = ∠C. 又
∵ AB = CD,∠AFB = ∠CED = 90°,
∴ △ABF≌△CDE(AAS),
∴ BF = DE = b,CE = AF = c.
∵ AE = AD - DE = a - b,
∴ EF = AF - AE = c - (a - b) = c - a + b. 故选 B.
2 [2025 河北唐山期中,较难]已知$∠AOB= 90^{\circ }$,$OA= OB$,直线$l是经过∠AOB顶点O$的一条直线($l$不与角的两边重合),作$AC⊥l$,$BD⊥l$,垂足分别为$C$,$D$。甲、乙两位同学给出自己的结论:
甲:当直线$l穿过∠AOB$内部时,$DC= BD-AC$;
乙:当直线$l在∠AOB$外部时,$DC= BD+AC$。
对于上述的两个结论,下列说法正确的是( )
A.只有甲正确
B.只有乙正确
C.甲、乙都正确
D.甲、乙都不正确
甲:当直线$l穿过∠AOB$内部时,$DC= BD-AC$;
乙:当直线$l在∠AOB$外部时,$DC= BD+AC$。
对于上述的两个结论,下列说法正确的是( )
A.只有甲正确
B.只有乙正确
C.甲、乙都正确
D.甲、乙都不正确
答案:
B 【解析】
(1)如图
(1),当直线 l 穿过∠AOB 内部,且点 C 在点 D 的左侧时,
∵ AC⊥l,BD⊥l,
∴ ∠ACO = ∠ODB = 90°,
∴ ∠A + ∠AOC = 90°.
∵ ∠AOB = 90°,
∴ ∠AOC + ∠BOD = 90°,
∴ ∠A = ∠BOD. 在△ACO 和△ODB 中,{∠ACO = ∠ODB,∠A = ∠BOD,OA = OB},
∴ △ACO ≌ △ODB(AAS),
∴ AC = OD,OC = BD,
∴ 此时 CD = OD - OC = AC - BD,故甲不正确.
如图
(2),当直线 l 在∠AOB 外部时,
∵ AC⊥l,BD⊥l,
∴ ∠ACO = ∠ODB = 90°,
∴ ∠A + ∠AOC = 90°.
∵ ∠AOB = 90°,
∴ ∠AOC + ∠BOD = 90°,
∴ ∠A = ∠BOD. 在△ACO 和△ODB 中,{∠ACO = ∠ODB,∠A = ∠BOD,OA = OB},
∴ △ACO≌△ODB(AAS),
∴ AC = OD,OC = BD,
∴ CD = OD + OC = AC + BD,故乙正确. 故选 B.
B 【解析】
(1)如图
(1),当直线 l 穿过∠AOB 内部,且点 C 在点 D 的左侧时,
∵ AC⊥l,BD⊥l,
∴ ∠ACO = ∠ODB = 90°,
∴ ∠A + ∠AOC = 90°.
∵ ∠AOB = 90°,
∴ ∠AOC + ∠BOD = 90°,
∴ ∠A = ∠BOD. 在△ACO 和△ODB 中,{∠ACO = ∠ODB,∠A = ∠BOD,OA = OB},
∴ △ACO ≌ △ODB(AAS),
∴ AC = OD,OC = BD,
∴ 此时 CD = OD - OC = AC - BD,故甲不正确.

如图
(2),当直线 l 在∠AOB 外部时,
∵ AC⊥l,BD⊥l,
∴ ∠ACO = ∠ODB = 90°,
∴ ∠A + ∠AOC = 90°.
∵ ∠AOB = 90°,
∴ ∠AOC + ∠BOD = 90°,
∴ ∠A = ∠BOD. 在△ACO 和△ODB 中,{∠ACO = ∠ODB,∠A = ∠BOD,OA = OB},
∴ △ACO≌△ODB(AAS),
∴ AC = OD,OC = BD,
∴ CD = OD + OC = AC + BD,故乙正确. 故选 B.

3 [2025 江苏南京质检,中]如图,在正方形$ABCD$中,$AB= 11$,$E在AB$边上,$F在BC$边上,且$BF= 3$,将$EF绕着点F顺时针旋转90^{\circ }得到GF$,连接$DG$,则$DG$的长的最小值为______。
答案:
8 【解析】如图,过点 G 作 GH⊥BC,垂足为 H,
∴ ∠GHF = 90°.
∵ 四边形 ABCD 是正方形,
∴ AB = CD = 11,∠B = 90°,
∴ ∠B = ∠GHF = 90°. 由旋转得 EF = FG,∠EFG = 90°,
∴ ∠EFB + ∠GFH = 90°.
∵ ∠BEF + ∠BFE = 90°,
∴ ∠BEF = ∠GFH,
∴ △EBF≌△FHG(AAS),
∴ BF = GH = 3,
∴ 点 G 在与 BC 平行且与 BC 的距离为 3 的直线上,
∴ 当点 G 在 CD 边上时,DG 的长最小,此时 DG = 11 - 3 = 8,
∴ DG 的长的最小值为 8,故答案为 8.
8 【解析】如图,过点 G 作 GH⊥BC,垂足为 H,
∴ ∠GHF = 90°.
∵ 四边形 ABCD 是正方形,
∴ AB = CD = 11,∠B = 90°,
∴ ∠B = ∠GHF = 90°. 由旋转得 EF = FG,∠EFG = 90°,
∴ ∠EFB + ∠GFH = 90°.
∵ ∠BEF + ∠BFE = 90°,
∴ ∠BEF = ∠GFH,
∴ △EBF≌△FHG(AAS),
∴ BF = GH = 3,
∴ 点 G 在与 BC 平行且与 BC 的距离为 3 的直线上,
∴ 当点 G 在 CD 边上时,DG 的长最小,此时 DG = 11 - 3 = 8,
∴ DG 的长的最小值为 8,故答案为 8.

4 [2025 江苏南通期中,中]如图所示,$AC平分∠BAD$,$∠B+∠D= 180^{\circ }$,$CE⊥AD于点E$,$AD= 13cm$,$AB= 7cm$,则$DE$的长度为______$cm$。
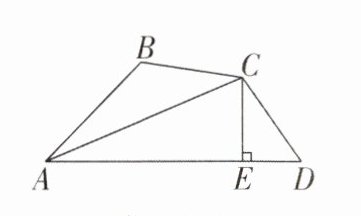

答案:
3 【解析】如图,过 C 作 CF⊥AB 交 AB 的延长线于点 F.
∵ AC 平分∠BAD,
∴ ∠FAC = ∠EAC.
∵ CE⊥AD,CF⊥AB,
∴ ∠BFC = ∠CEA = ∠CED = 90°. 在△AFC 和△AEC 中,{∠FAC = ∠EAC,∠CFA = ∠CEA,AC = AC},
∴ △AFC≌△AEC(AAS),
∴ AF = AE,CF = CE.
∵ ∠ABC + ∠D = 180°,∠ABC + ∠FBC = 180°,
∴ ∠FBC = ∠EDC,
∴ △FBC≌△EDC(AAS),
∴ BF = ED,
∴ AD + AB = AE + ED + AF - BF = 2AE. 又
∵ AD = 13 cm,AB = 7 cm,
∴ 2AE = 13 + 7 = 20(cm),
∴ AE = 10 cm,
∴ DE = AD - AE = 13 - 10 = 3(cm). 故答案为 3.
3 【解析】如图,过 C 作 CF⊥AB 交 AB 的延长线于点 F.
∵ AC 平分∠BAD,
∴ ∠FAC = ∠EAC.
∵ CE⊥AD,CF⊥AB,
∴ ∠BFC = ∠CEA = ∠CED = 90°. 在△AFC 和△AEC 中,{∠FAC = ∠EAC,∠CFA = ∠CEA,AC = AC},
∴ △AFC≌△AEC(AAS),
∴ AF = AE,CF = CE.
∵ ∠ABC + ∠D = 180°,∠ABC + ∠FBC = 180°,
∴ ∠FBC = ∠EDC,
∴ △FBC≌△EDC(AAS),
∴ BF = ED,
∴ AD + AB = AE + ED + AF - BF = 2AE. 又
∵ AD = 13 cm,AB = 7 cm,
∴ 2AE = 13 + 7 = 20(cm),
∴ AE = 10 cm,
∴ DE = AD - AE = 13 - 10 = 3(cm). 故答案为 3.

5 [较难]如图,在$△ABC$中,$∠ACB= 90^{\circ }$,$AC= 7cm$,$BC= 3cm$,$CD为AB$边上的高,点$E从点B$出发,在直线$BC上以2cm/s$的速度运动,过点$E作BC的垂线交直线CD于点F$,当点$E$运动______$s$时,$CF= AB$。
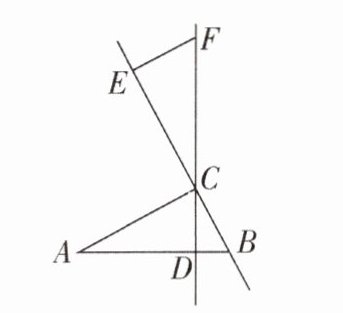

答案:
2 或 5 【解析】
∵ ∠ACB = 90°,
∴ ∠A + ∠CBD = 90°.
∵ CD 为 AB 边上的高,
∴ ∠CDB = 90°,
∴ ∠BCD + ∠CBD = 90°,
∴ ∠A = ∠BCD.
∵ ∠BCD = ∠ECF,
∴ ∠ECF = ∠A.
∵ 过点 E 作 BC 的垂线交直线 CD 于点 F,
∴ ∠CEF = 90° = ∠ACB. 在△CEF 和△ACB 中,{∠ECF = ∠A,∠CEF = ∠ACB,CF = AB},
∴ △CEF≌△ACB(AAS),
∴ CE = AC = 7 cm. 如图,分两种情况:①当点 E 在线段 BC 的延长线上运动时,BE = CE + BC = 7 + 3 = 10(cm).
∵ 点 E 从点 B 出发,在直线 BC 上以 2 cm/s 的,
∴ E 运动了$\frac{10}{2}$ = 5(s);②当点 E 在线段 CB 的延长线上运动时,BE' = CE' - BC = 7 - 3 = 4(cm),
∴ E 运动了$\frac{4}{2}$ = 2(s). 故答案为 2 或 5.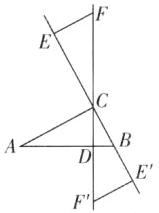
思路分析
(2)由 FD//BC 得到一对同位角相等,再结合
(1)的结论等量代换得到一对角相等,然后根据 AF 为∠BAE 的平分线得到一对角相等,结合 AF = AF,利用“AAS”证明△ABF≌△ADF,利用全等三角形对应边相等得到 AB = AD,由 DC = AC - AD 即可求解.
易错警示 注意点 E 的位置有两种情况,可以在线段 BC 的延长线上,也可以在线段 CB 的延长线上.
2 或 5 【解析】
∵ ∠ACB = 90°,
∴ ∠A + ∠CBD = 90°.
∵ CD 为 AB 边上的高,
∴ ∠CDB = 90°,
∴ ∠BCD + ∠CBD = 90°,
∴ ∠A = ∠BCD.
∵ ∠BCD = ∠ECF,
∴ ∠ECF = ∠A.
∵ 过点 E 作 BC 的垂线交直线 CD 于点 F,
∴ ∠CEF = 90° = ∠ACB. 在△CEF 和△ACB 中,{∠ECF = ∠A,∠CEF = ∠ACB,CF = AB},
∴ △CEF≌△ACB(AAS),
∴ CE = AC = 7 cm. 如图,分两种情况:①当点 E 在线段 BC 的延长线上运动时,BE = CE + BC = 7 + 3 = 10(cm).
∵ 点 E 从点 B 出发,在直线 BC 上以 2 cm/s 的,
∴ E 运动了$\frac{10}{2}$ = 5(s);②当点 E 在线段 CB 的延长线上运动时,BE' = CE' - BC = 7 - 3 = 4(cm),
∴ E 运动了$\frac{4}{2}$ = 2(s). 故答案为 2 或 5.

思路分析
(2)由 FD//BC 得到一对同位角相等,再结合
(1)的结论等量代换得到一对角相等,然后根据 AF 为∠BAE 的平分线得到一对角相等,结合 AF = AF,利用“AAS”证明△ABF≌△ADF,利用全等三角形对应边相等得到 AB = AD,由 DC = AC - AD 即可求解.
易错警示 注意点 E 的位置有两种情况,可以在线段 BC 的延长线上,也可以在线段 CB 的延长线上.
6 核心素养 几何直观 [2025 江苏泰州调研,较难]小聪同学学了《全等三角形的判定》后,在已知条件不变的情况下,对一道练习题进行了拓展探究。
【原题呈现】如图(1),$AC⊥BC$,$DC⊥EC$,$AC= BC$,$DC= EC$。图中$AE$,$BD$有怎样的数量关系和位置关系?试证明你的结论。
(1)解决上述问题;
(2)如图(2),连接$BE$,若$BC$,$EC分别平分∠DBE$,$∠AEB$,求$∠BCE$的度数;
(3)如图(3),连接$AD$,$BE$,过点$C作CF⊥BE于点F$,延长$FC交AD于点G$,求证:点$G是AD$的中点。
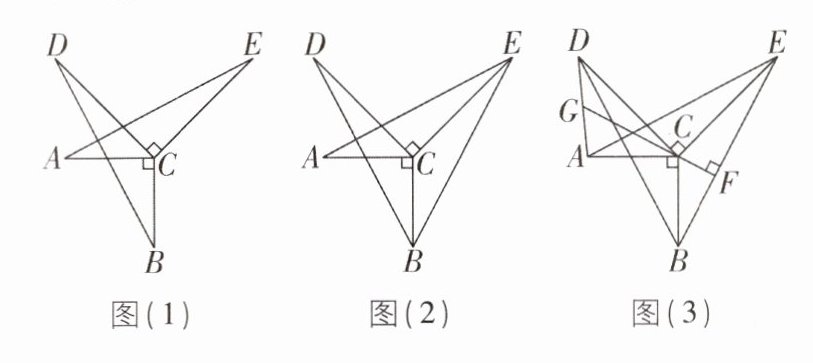
【原题呈现】如图(1),$AC⊥BC$,$DC⊥EC$,$AC= BC$,$DC= EC$。图中$AE$,$BD$有怎样的数量关系和位置关系?试证明你的结论。
(1)解决上述问题;
(2)如图(2),连接$BE$,若$BC$,$EC分别平分∠DBE$,$∠AEB$,求$∠BCE$的度数;
(3)如图(3),连接$AD$,$BE$,过点$C作CF⊥BE于点F$,延长$FC交AD于点G$,求证:点$G是AD$的中点。

答案:
(1)【解】AE = BD,AE⊥BD. 证明:如图
(1),设 AE,BD 相交于点 P,AE,CD 相交于点 K.
∵ AC⊥BC,DC⊥EC,
∴ ∠ACB = ∠DCE = 90°,
∴ ∠ACB + ∠ACD = ∠DCE + ∠ACD,即∠BCD = ∠ACE. 在△ACE 和△BCD 中,{AC = BC,∠ACE = ∠BCD,EC = DC},
∴ △ACE≌△BCD(SAS),
∴ AE = BD,∠AEC = ∠BDC.
∵ ∠CKE = ∠PKD,
∴ ∠DPK = ∠DCE = 90°,
∴ AE⊥BD.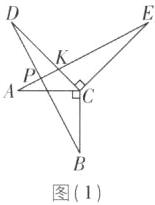
(2)【解】
∵ BC,EC 分别平分∠DBE,∠AEB,
∴ ∠CBD = ∠CBE,∠CEA = ∠CEB.
∵ △ACE≌△BCD,
∴ ∠CAE = ∠CBD,
∴ ∠CAE = ∠CBE. 又
∵ CE = CE,
∴ △CAE≌△CBE(AAS),
∴ ∠ACE = ∠BCE.
∵ ∠ACB = 90°,
∴ ∠BCE = ∠ACE = $\frac{360° - 90°}{2}$ = 135°.
(3)【证明】如图
(2),过点 D 作 DH⊥FG 交 FG 的延长线于点 H,过点 A 作 AM⊥FG 于点 M,则∠DHG = ∠AMG = ∠AMC = 90°.
∵ CF⊥BE,
∴ ∠CFE = ∠CFB = 90°,
∴ ∠FCE + ∠CEF = 90°.
∵ ∠DCE = 90°,
∴ ∠DCH + ∠FCE = 90°,
∴ ∠DCH = ∠CEF. 又
∵ ∠CHD = ∠CFE = 90°,DC = EC,
∴ △CHD≌△EFC(AAS),
∴ DH = CF. 同理可得△AMC≌△CFB,
∴ AM = CF,
∴ DH = AM.
∵ ∠DHG = ∠AMG = 90°,∠DGH = ∠AGM,
∴ △DGH≌△AGM(AAS),
∴ DG = AG,即点 G 是 AD 的中点.
(1)【解】AE = BD,AE⊥BD. 证明:如图
(1),设 AE,BD 相交于点 P,AE,CD 相交于点 K.
∵ AC⊥BC,DC⊥EC,
∴ ∠ACB = ∠DCE = 90°,
∴ ∠ACB + ∠ACD = ∠DCE + ∠ACD,即∠BCD = ∠ACE. 在△ACE 和△BCD 中,{AC = BC,∠ACE = ∠BCD,EC = DC},
∴ △ACE≌△BCD(SAS),
∴ AE = BD,∠AEC = ∠BDC.
∵ ∠CKE = ∠PKD,
∴ ∠DPK = ∠DCE = 90°,
∴ AE⊥BD.

(2)【解】
∵ BC,EC 分别平分∠DBE,∠AEB,
∴ ∠CBD = ∠CBE,∠CEA = ∠CEB.
∵ △ACE≌△BCD,
∴ ∠CAE = ∠CBD,
∴ ∠CAE = ∠CBE. 又
∵ CE = CE,
∴ △CAE≌△CBE(AAS),
∴ ∠ACE = ∠BCE.
∵ ∠ACB = 90°,
∴ ∠BCE = ∠ACE = $\frac{360° - 90°}{2}$ = 135°.
(3)【证明】如图
(2),过点 D 作 DH⊥FG 交 FG 的延长线于点 H,过点 A 作 AM⊥FG 于点 M,则∠DHG = ∠AMG = ∠AMC = 90°.
∵ CF⊥BE,
∴ ∠CFE = ∠CFB = 90°,
∴ ∠FCE + ∠CEF = 90°.
∵ ∠DCE = 90°,
∴ ∠DCH + ∠FCE = 90°,
∴ ∠DCH = ∠CEF. 又
∵ ∠CHD = ∠CFE = 90°,DC = EC,
∴ △CHD≌△EFC(AAS),
∴ DH = CF. 同理可得△AMC≌△CFB,
∴ AM = CF,
∴ DH = AM.
∵ ∠DHG = ∠AMG = 90°,∠DGH = ∠AGM,
∴ △DGH≌△AGM(AAS),
∴ DG = AG,即点 G 是 AD 的中点.

查看更多完整答案,请扫码查看


