第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2025 北京海淀区期中,中]如图,在直角三角形 ABC 中,∠ABC = 90°,点 D 沿 CB 自点 C 向点 B 运动(点 D 与点 C,B 不重合),作 BE⊥AD 于点 E,CF⊥AD 的延长线于点 F,在点 D 的运动过程中,BE + CF 的值逐渐(
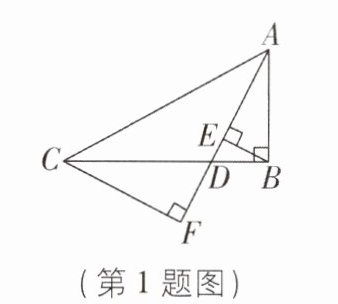
A.变小
B.变大
C.不变
D.无法确定
B
)
A.变小
B.变大
C.不变
D.无法确定
答案:
B 【解析】
∵ △ABC 的面积不变,点 D 沿 CB 自点 C 向点 B 运动时 AD 逐渐减小,
∴ BE+CF 的值逐渐变大,故选 B.
∵ △ABC 的面积不变,点 D 沿 CB 自点 C 向点 B 运动时 AD 逐渐减小,
∴ BE+CF 的值逐渐变大,故选 B.
如图,点 E 是长方形 ABCD 内任意一点,连接 AE,BE,CE,DE 把长方形分成 4 个三角形,将△ABE,△BCE,△CDE,△ADE 的面积分别记为$ S_1,S_2,S_3,S_4.$已知长方形的面积,则一定可求出的值是(
$A.S_1$
$B.S_1 + S_2$
$C.S_1 + S_2 + S_3$
$D.S_1 + S_3$
D
)$A.S_1$
$B.S_1 + S_2$
$C.S_1 + S_2 + S_3$
$D.S_1 + S_3$
答案:
D 【解析】设△ABE 的边 AB 上的高为 h₁,△BCE 的边 BC 上的高为 h₂,△CDE 的边 CD 上的高为 h₃,△ADE 的边 AD 上的高为 h₄.
∵ 长方形 ABCD 中,AB=CD,AD=BC,
∴ h₁+h₃=BC,h₂+h₄=AB.
∵ S₁=$\frac{1}{2}$AB·h₁,S₂=$\frac{1}{2}$BC·h₂,S₃=$\frac{1}{2}$CD·h₃,S₄=$\frac{1}{2}$AD·h₄,已知长方形的面积,即已知 AB·BC 的值,
∴ S₁ 不可求,故 A 选项不符合题意;S₁+S₂=$\frac{1}{2}$(AB·h₁+BC·h₂)不可求,故 B 选项不符合题意;S₁+S₂+S₃=$\frac{1}{2}$(AB·h₁+BC·h₂+CD·h₃)=$\frac{1}{2}$(AB·BC+BC·h₂)不可求,故 C 选项不符合题意;S₁+S₃=$\frac{1}{2}$AB·h₁$\frac{+1}{2}$CD·h₃=$\frac{1}{2}$AB·BC 可求,故 D 选项符合题意. 故选 D.
∵ 长方形 ABCD 中,AB=CD,AD=BC,
∴ h₁+h₃=BC,h₂+h₄=AB.
∵ S₁=$\frac{1}{2}$AB·h₁,S₂=$\frac{1}{2}$BC·h₂,S₃=$\frac{1}{2}$CD·h₃,S₄=$\frac{1}{2}$AD·h₄,已知长方形的面积,即已知 AB·BC 的值,
∴ S₁ 不可求,故 A 选项不符合题意;S₁+S₂=$\frac{1}{2}$(AB·h₁+BC·h₂)不可求,故 B 选项不符合题意;S₁+S₂+S₃=$\frac{1}{2}$(AB·h₁+BC·h₂+CD·h₃)=$\frac{1}{2}$(AB·BC+BC·h₂)不可求,故 C 选项不符合题意;S₁+S₃=$\frac{1}{2}$AB·h₁$\frac{+1}{2}$CD·h₃=$\frac{1}{2}$AB·BC 可求,故 D 选项符合题意. 故选 D.
3 [2025 江苏宿迁质检,中]如图,在△ABC 中,AD 为 BC 边上的中线,DE⊥AB 于点 E,DF⊥AC 于点 F,AB = 3,AC = 4,DF = 1.5,则 DE = ______.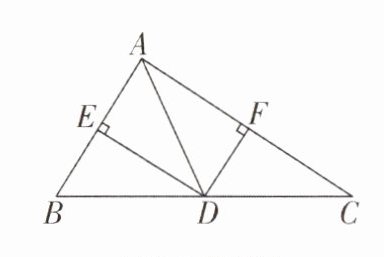

2
答案:
∵AD为BC边上的中线,
∴BD=DC,
∴S△ABD=S△ADC.
∵DE⊥AB,DF⊥AC,AB=3,AC=4,DF=1.5,
∴$\frac{1}{2}AB·DE=\frac{1}{2}AC·DF$,
即$\frac{1}{2}×3×DE=\frac{1}{2}×4×1.5$,
解得DE=2.
故答案为2.
∵AD为BC边上的中线,
∴BD=DC,
∴S△ABD=S△ADC.
∵DE⊥AB,DF⊥AC,AB=3,AC=4,DF=1.5,
∴$\frac{1}{2}AB·DE=\frac{1}{2}AC·DF$,
即$\frac{1}{2}×3×DE=\frac{1}{2}×4×1.5$,
解得DE=2.
故答案为2.
4 [2025 湖北武汉调研,中]如图,点 G 为△ABC 的重心,CF⊥BE 于 G,若 AG×BC = 16,则△BGC 面积的最大值是______.


4
答案:
∵G是△ABC的重心,
∴AG=2GD。
∵CF⊥BE于G,即CG⊥BG,
∴S△BGC=$\frac{1}{2}$×BG×CG。
又AG×BC=16,AG=2GD,
∴GD=$\frac{1}{2}$AG,BC=$\frac{16}{AG}$。
当GD⊥BC时,S△BGC=$\frac{1}{2}$×BC×GD=$\frac{1}{2}$×$\frac{16}{AG}$×$\frac{1}{2}$AG=4。
故△BGC面积的最大值是4。
4
∵G是△ABC的重心,
∴AG=2GD。
∵CF⊥BE于G,即CG⊥BG,
∴S△BGC=$\frac{1}{2}$×BG×CG。
又AG×BC=16,AG=2GD,
∴GD=$\frac{1}{2}$AG,BC=$\frac{16}{AG}$。
当GD⊥BC时,S△BGC=$\frac{1}{2}$×BC×GD=$\frac{1}{2}$×$\frac{16}{AG}$×$\frac{1}{2}$AG=4。
故△BGC面积的最大值是4。
4
(1)通过观察,可以发现△ABC 是(
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 直角三角形或锐角三角形
(2)仅利用无刻度的直尺画出△ABC 的中线 AD 与角平分线 CE.
(3)△ABC 的面积为______
C
)A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 直角三角形或锐角三角形
(2)仅利用无刻度的直尺画出△ABC 的中线 AD 与角平分线 CE.
如图,线段 AD 即为所求作的△ABC 的中线,线段 CE 即为所求作的△ABC 的角平分线.
(3)△ABC 的面积为______
12
,△ABD 的面积为______6
.
答案:
【解】
(1)由格点可知,∠ACB=45°+45°=90°,
∴ △ABC 是直角三角形,故选 C.
(2)如图,线段 AD 即为所求作的△ABC 的中线,线段 CE 即为所求作的△ABC 的角平分线.
(3)由题意知 S△ABC=(3+4)×$\frac{7}{2}$ - 3×$\frac{3}{2}$ - 4×$\frac{4}{2}$=12,
∴ S△ABD=$\frac{1}{2}$S△ABC=6,故答案为 12,6.
(1)由格点可知,∠ACB=45°+45°=90°,
∴ △ABC 是直角三角形,故选 C.
(2)如图,线段 AD 即为所求作的△ABC 的中线,线段 CE 即为所求作的△ABC 的角平分线.
(3)由题意知 S△ABC=(3+4)×$\frac{7}{2}$ - 3×$\frac{3}{2}$ - 4×$\frac{4}{2}$=12,
∴ S△ABD=$\frac{1}{2}$S△ABC=6,故答案为 12,6.
6 核心素养 模型观念 [2025 江苏南京质检,较难]如图(1),有一块三角形菜地,若从顶点 A 修一条笔直的小路交 BC 于点 D,小路正好将菜地分成面积相等的两部分.
(1)找出 D 点的位置并说明理由.
(2)假设在菜地中有一点 E,如图(2)所示,BC 上是否存在点 F,使折线 A - E - F 将△ABC 分为面积相等的两部分?若存在,请找出 F 点的位置,并说明理由.
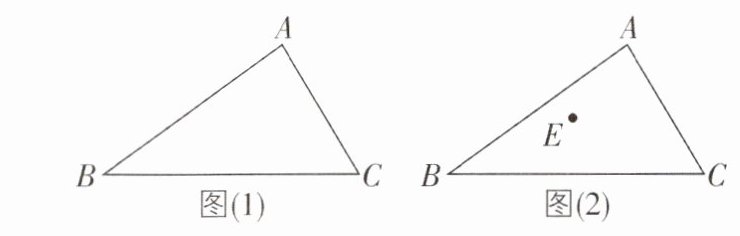
(1)找出 D 点的位置并说明理由.
(2)假设在菜地中有一点 E,如图(2)所示,BC 上是否存在点 F,使折线 A - E - F 将△ABC 分为面积相等的两部分?若存在,请找出 F 点的位置,并说明理由.

答案:
$(1)$ 找出$D$点的位置并说明理由
解:$D$点是$BC$边的中点。
理由:根据三角形面积公式$S = \frac{1}{2}ah$($a$表示底,$h$表示这条底对应的高)。
在$\triangle ABC$中,$\triangle ABD$与$\triangle ACD$的高相同(都是$A$到$BC$的距离),当$BD = CD$时,根据三角形面积公式$S_{\triangle ABD}=\frac{1}{2}BD× h$,$S_{\triangle ACD}=\frac{1}{2}CD× h$,因为$BD = CD$,所以$S_{\triangle ABD}=S_{\triangle ACD}$,即$D$为$BC$中点时,小路$AD$正好将菜地分成面积相等的两部分。
$(2)$ 判断$BC$上是否存在点$F$,使折线$A - E - F$将$\triangle ABC$分为面积相等的两部分,并找出$F$点的位置,说明理由
解:存在。
连接$AE$,过点$D$($D$为$BC$中点)作$DF// AE$交$BC$于点$F$,则点$F$即为所求。
理由:连接$AF$,因为$DF// AE$,所以$S_{\triangle ADE}=S_{\triangle AFE}$(同底等高的三角形面积相等,$\triangle ADE$与$\triangle AFE$以$AE$为底时,高相等)。
又因为$D$是$BC$中点,所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$。
$S_{ABEF}=S_{\triangle ABD}-S_{\triangle ADE}+S_{\triangle AFE}=S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$,$S_{AFCC}=S_{\triangle ACD}+S_{\triangle ADE}-S_{\triangle AFE}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$。
所以折线$A - E - F$将$\triangle ABC$分为面积相等的两部分。
综上,$(1)$$\boldsymbol{D}$为$\boldsymbol{BC}$中点;$(2)$存在,连接$\boldsymbol{AE}$,过$\boldsymbol{BC}$中点$\boldsymbol{D}$作$\boldsymbol{DF// AE}$交$\boldsymbol{BC}$于点$\boldsymbol{F}$,点$\boldsymbol{F}$即为所求 。
解:$D$点是$BC$边的中点。
理由:根据三角形面积公式$S = \frac{1}{2}ah$($a$表示底,$h$表示这条底对应的高)。
在$\triangle ABC$中,$\triangle ABD$与$\triangle ACD$的高相同(都是$A$到$BC$的距离),当$BD = CD$时,根据三角形面积公式$S_{\triangle ABD}=\frac{1}{2}BD× h$,$S_{\triangle ACD}=\frac{1}{2}CD× h$,因为$BD = CD$,所以$S_{\triangle ABD}=S_{\triangle ACD}$,即$D$为$BC$中点时,小路$AD$正好将菜地分成面积相等的两部分。
$(2)$ 判断$BC$上是否存在点$F$,使折线$A - E - F$将$\triangle ABC$分为面积相等的两部分,并找出$F$点的位置,说明理由
解:存在。
连接$AE$,过点$D$($D$为$BC$中点)作$DF// AE$交$BC$于点$F$,则点$F$即为所求。
理由:连接$AF$,因为$DF// AE$,所以$S_{\triangle ADE}=S_{\triangle AFE}$(同底等高的三角形面积相等,$\triangle ADE$与$\triangle AFE$以$AE$为底时,高相等)。
又因为$D$是$BC$中点,所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$。
$S_{ABEF}=S_{\triangle ABD}-S_{\triangle ADE}+S_{\triangle AFE}=S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$,$S_{AFCC}=S_{\triangle ACD}+S_{\triangle ADE}-S_{\triangle AFE}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$。
所以折线$A - E - F$将$\triangle ABC$分为面积相等的两部分。
综上,$(1)$$\boldsymbol{D}$为$\boldsymbol{BC}$中点;$(2)$存在,连接$\boldsymbol{AE}$,过$\boldsymbol{BC}$中点$\boldsymbol{D}$作$\boldsymbol{DF// AE}$交$\boldsymbol{BC}$于点$\boldsymbol{F}$,点$\boldsymbol{F}$即为所求 。
查看更多完整答案,请扫码查看


