《2025年初中必刷题八年级数学上册苏科版》

有甲、乙、丙三人,它们所在的位置不同,他们三人都以相同的单位长度建立不同的平面直角坐标系,甲说:“如果以我为坐标原点,乙的位置是$(4,3)$.”丙说:“如果以我为坐标原点,乙的位置是$(-3,-4)$. ”如果以乙为坐标原点,甲和丙的位置分别是 (D)
A.$(3,4),(-3,-4)$
B.$(4,-3),(3,-4)$
C.$(-3,-4),(4,3)$
D.$(-4,-3),(3,4)$

答案： 1.D 【解析】以甲为坐标原点，乙的位置是(4,3)，则以乙为坐标原点，甲的位置是(-4,-3)；以丙为坐标原点，乙的位置是(-3,-4)，则以乙为坐标原点，丙的位置是(3,4).故选D.

2 新素材 [2025 山东临沂期末]2024 年 5 月 5 日在四川成都举行的尤伯杯羽毛球团体赛决赛中,中国队第 16 次夺得冠军.如图(1)是比赛场馆图,图(2)是场馆某正方形座位示意图,小李、小亮、小东的座位如图所示(网格中,每个小正方形的边长都是 1).若小亮的座位用$(-1,0)$表示,小李的座位用$(1,3)$表示,则小东的座位可以表示为____.

答案：
2.(3,-1) 【解析】由题意建立平面直角坐标系如图，则小东的座位可以表示为(3,-1)，故答案为(3,-1).

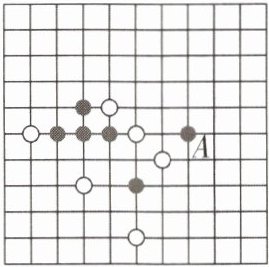
3 [2024 湖南长沙调研]五子棋是一种两人对弈的棋类游戏,规则是在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者正方形对角线的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.将每个棋子看成一个点,每个小方格的边长记为 1.若黑子 A 的坐标为$(7,5)$,为了不让白方获胜,此时黑方应该将黑子下在坐标为____的位置.

答案：
3.(3,7)或(7,3)
【解析】根据题意，建立平面直线坐标系如图所示.因为白方已有(4,6),(5,5),(6,4)三点在一条直线上，所以黑方只有在此三点两端任加一点才可保证不会让白方获胜，即此时黑方应该将黑子下在坐标为(3,7)或(7,3)的位置.故答案为(3,7)或(7,3).

4 [2024 江苏苏州姑苏区调研]如图,方格纸中每个小方格都是边长为 1 个单位长度的正方形,学校位置坐标为$A(2,1)$,图书馆位置坐标为$B(-1,-2)$,解答下列问题:
(1)在图中建立平面直角坐标系,并标出坐标原点 O;
(2)若体育馆位置坐标为$C(1,3)$,请在坐标系中标出体育馆的位置 C;
(3)点 C 绕原点顺时针旋转$90^{\circ }$得到点 D,直接写出点 D 的坐标;
(4)顺次连接学校、图书馆、体育馆,得到$\triangle ABC$,求$\triangle ABC$的面积.

答案：
4.【解】
(1)如图所示.
(2)如图，点C即为所求.
(3)如图，D(3,-1).
(4)$S_{\triangle ABC}=3×5-\frac {1}{2}×2×5-\frac {1}{2}×3×3-\frac {1}{2}×1×2=4.5.$

5 [2024 甘肃酒泉期中]如图所示,在长方形 ABCD 中,已知$AB= 6,AD= 4$,在长方形 ABCD 外画$\triangle ABE$,使$AE= BE= 5$,请建立适当的平面直角坐标系,并求出各顶点的坐标.
 

答案：
5.【解】如图，以D为坐标原点，CD和AD所在直线为x轴和y轴建立平面直角坐标系，则A点的坐标是(0,4)，B点的坐标是(6,4)，C点的坐标是(6,0)，D点的坐标是(0,0).过点E作$EG⊥CD$交AB于点F，交CD于点G.
∵ AE = BE，$\therefore AF=\frac {1}{2}AB=\frac {1}{2}×6=3$.在$Rt\triangle AEF$中，$EF=\sqrt {AE^{2}-AF^{2}}=\sqrt {5^{2}-3^{2}}=4$，$\therefore EG=4 + 4 = 8$，
∴ E的坐标是(3,8).(答案不唯一)