第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
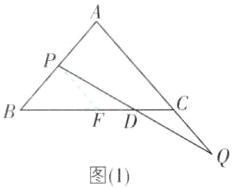
1 [2025山东菏泽调研,较难]如图,在$\triangle ABC$中,$AB= AC$,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,当点P移动至点A时,P,Q两点同时停止移动.已知点P,Q移动的速度相同,PQ与BC相交于点D.
(1)如图(1),试说明:$PD= QD$.
(2)如图(2),过点P作BC的垂线,垂足为E,点P,Q在移动的过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.

(1)如图(1),试说明:$PD= QD$.
(2)如图(2),过点P作BC的垂线,垂足为E,点P,Q在移动的过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.

答案:
1.[解]
(1)过P点作PF//AC交BC于F,如图
(1).
因为点P和点Q同时出发,且移动的速度相同,所以BP=CQ.因为PF//AQ,所以∠PFB=∠ACB,∠DPF=∠DQC.因为AB=AC,所以∠B=∠ACB,所以∠B=∠PFB,所以BP=PF,所以PF=CQ.
因为∠PDF=∠QDC,PF=CQ,∠DPF=∠DQC,
所以△PFD≌△QCD,所以PD=QD.
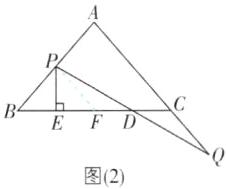
(2)存在,ED的长度保持不变.理由如下:
过点P作PF//AQ交BC于点F,如图
(2).由
(1)知PB=PF.
因为PE⊥BF,所以BE=EF.
由
(1)知△PFD≌△QCD,所以FD=DC,
所以ED=EF+FD=BE+DC=$\frac{1}{2}$BC,
所以ED的长度保持不变.
1.[解]
(1)过P点作PF//AC交BC于F,如图
(1).
因为点P和点Q同时出发,且移动的速度相同,所以BP=CQ.因为PF//AQ,所以∠PFB=∠ACB,∠DPF=∠DQC.因为AB=AC,所以∠B=∠ACB,所以∠B=∠PFB,所以BP=PF,所以PF=CQ.
因为∠PDF=∠QDC,PF=CQ,∠DPF=∠DQC,
所以△PFD≌△QCD,所以PD=QD.


(2)存在,ED的长度保持不变.理由如下:
过点P作PF//AQ交BC于点F,如图
(2).由
(1)知PB=PF.
因为PE⊥BF,所以BE=EF.
由
(1)知△PFD≌△QCD,所以FD=DC,
所以ED=EF+FD=BE+DC=$\frac{1}{2}$BC,
所以ED的长度保持不变.
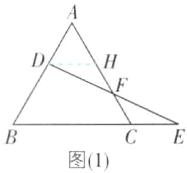
2 [2025河南郑州期末,较难]如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E.
(1)如图(1),若$FE= FD$,试说明$AD= CE$.
(2)如图(2),若$FE= FD,AB= 2$,过点D作$DG\perp AC$,垂足为点G,问GF的长是否为定值?若是,请求出这个定值;若不是,请说明理由.
(1)如图(1),若$FE= FD$,试说明$AD= CE$.
(2)如图(2),若$FE= FD,AB= 2$,过点D作$DG\perp AC$,垂足为点G,问GF的长是否为定值?若是,请求出这个定值;若不是,请说明理由.

答案:
2.[解]
(1)如图
(1),过点D作DH//BC交AC于点H,所以∠DHF=∠ECF.在△DHF和△ECF中,{∠DHF=∠ECF,∠HFD=∠CFE,DF=EF,所以△DHF≌△ECF,所以DH=CE.
因为△ABC是等边三角形,
所以∠ABC=∠A=60°.
因为DH//BC,所以∠ADH=∠ABC=60°=∠A,所以△ADH是等边三角形,所以AD=DH.因为DH=CE,所以AD=CE.
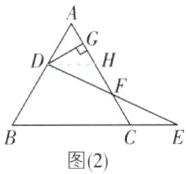
(2)GF的长是定值.如图
(2),
过点D作DH//BC交AC于点H.
由
(1)知△DHF≌△ECF,
所以FH=FC=$\frac{1}{2}$CH.
由
(1)得△ADH是等边三角形,所以AD=AH,
所以CH=BD,所以FH=$\frac{1}{2}$BD.
因为DG⊥AC,所以AG=HG=$\frac{1}{2}$AH=$\frac{1}{2}$AD,
所以GF=HG+HF=$\frac{1}{2}$AD+$\frac{1}{2}$BD=$\frac{1}{2}$(AD+BD)=$\frac{1}{2}$AB=1,即GF的长是定值,为1.
2.[解]
(1)如图
(1),过点D作DH//BC交AC于点H,所以∠DHF=∠ECF.在△DHF和△ECF中,{∠DHF=∠ECF,∠HFD=∠CFE,DF=EF,所以△DHF≌△ECF,所以DH=CE.
因为△ABC是等边三角形,
所以∠ABC=∠A=60°.
因为DH//BC,所以∠ADH=∠ABC=60°=∠A,所以△ADH是等边三角形,所以AD=DH.因为DH=CE,所以AD=CE.


(2)GF的长是定值.如图
(2),
过点D作DH//BC交AC于点H.
由
(1)知△DHF≌△ECF,
所以FH=FC=$\frac{1}{2}$CH.
由
(1)得△ADH是等边三角形,所以AD=AH,
所以CH=BD,所以FH=$\frac{1}{2}$BD.
因为DG⊥AC,所以AG=HG=$\frac{1}{2}$AH=$\frac{1}{2}$AD,
所以GF=HG+HF=$\frac{1}{2}$AD+$\frac{1}{2}$BD=$\frac{1}{2}$(AD+BD)=$\frac{1}{2}$AB=1,即GF的长是定值,为1.
3 [2025江苏泰州质检,中]如图,在$\triangle ABC$中,$\angle BAC= 2\angle B$,CD平分$\angle ACB$交AB于点D,求证:$AC+AD= BC$.


答案:
3.[证明]如图,在BC上截取CE=AC,连接DE.
∵CD是∠ACB的平分线,
∴∠ACD=∠ECD.在△ACD与△ECD中,{AC=EC,∠ACD=∠ECD,CD=CD,
∴△ACD≌△ECD(SAS),
∴∠CED=∠BAC=2∠B,AD=DE.又
∵∠CED=∠B+∠BDE,
∴∠BDE=∠B,
∴BE=DE=AD,
∴BC=CE+EB=AC+AD.

3.[证明]如图,在BC上截取CE=AC,连接DE.
∵CD是∠ACB的平分线,
∴∠ACD=∠ECD.在△ACD与△ECD中,{AC=EC,∠ACD=∠ECD,CD=CD,
∴△ACD≌△ECD(SAS),
∴∠CED=∠BAC=2∠B,AD=DE.又
∵∠CED=∠B+∠BDE,
∴∠BDE=∠B,
∴BE=DE=AD,
∴BC=CE+EB=AC+AD.

查看更多完整答案,请扫码查看


