第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
线段AB的垂直平分线上一点P到点A的距离为5,则点P到点B的距离(
A.等于5
B.大于5
C.小于5
D.无法确定
A
)A.等于5
B.大于5
C.小于5
D.无法确定
答案:
1.A [解析]
∵点P在线段AB的垂直平分线上,
∴PB=PA=5.故选A.
∵点P在线段AB的垂直平分线上,
∴PB=PA=5.故选A.
如图,在△ABC中,DE是边AC的垂直平分线,AE= 5cm,△ABD的周长为24cm,则△ABC的周长为
34
cm.
答案:
2.34 [解析]
∵DE是边AC的垂直平分线,AE=5cm,
∴AD=CD,AC=2AE=10cm.
∵△ABD的周长为24cm,
∴AB+BD+AD=AB+BD+CD=AB+BC=24cm,
∴C△ABC=AB+BC+AC=24+10=34(cm).故答案为34.
∵DE是边AC的垂直平分线,AE=5cm,
∴AD=CD,AC=2AE=10cm.
∵△ABD的周长为24cm,
∴AB+BD+AD=AB+BD+CD=AB+BC=24cm,
∴C△ABC=AB+BC+AC=24+10=34(cm).故答案为34.
3如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D,E.已知△ADE的周长为15cm,分别连接OA,OB,OC,若△OBC的周长为32cm,则OA的长为
8.5
cm.
答案:
3.8.5 [解析]
∵OM,ON分别为AB,AC的垂直平分线,
∴DA=DB,OA=OB,EA=EC,OA=OC.
∵△ADE的周长为15cm,
∴AD+DE+EA=15cm,
∴BD+DE+EC=15cm,即BC=15cm.
∵△OBC的周长为32cm,
∴OB+BC+OC=32cm,
∴OB+OC=32−15=17(cm),
∴OA=8.5cm.故答案为8.5.
∵OM,ON分别为AB,AC的垂直平分线,
∴DA=DB,OA=OB,EA=EC,OA=OC.
∵△ADE的周长为15cm,
∴AD+DE+EA=15cm,
∴BD+DE+EC=15cm,即BC=15cm.
∵△OBC的周长为32cm,
∴OB+BC+OC=32cm,
∴OB+OC=32−15=17(cm),
∴OA=8.5cm.故答案为8.5.
4[2025江苏苏州调研]如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB= CD,∠ABD= 116°,∠CDB= 28°,则∠OBD= ______°.
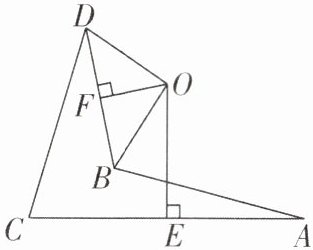

答案:
4.44 [解析]如图,连接OA,OC.
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∴∠OBD=∠ODB.在△AOB和△COD中,{OA=OC,AB=CD,OB=OD},
∴△AOB≌△COD(SSS),
∴∠ABO=∠CDO.
∵∠ABD=116°,∠CDB=28°,
∴∠ABO+∠OBD=116°,∠CDO−∠ODB=28°,即∠CDO−∠OBD=28°,
∴∠ABO=72°,∠OBD=44°,故答案为44.

4.44 [解析]如图,连接OA,OC.
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∴∠OBD=∠ODB.在△AOB和△COD中,{OA=OC,AB=CD,OB=OD},
∴△AOB≌△COD(SSS),
∴∠ABO=∠CDO.
∵∠ABD=116°,∠CDB=28°,
∴∠ABO+∠OBD=116°,∠CDO−∠ODB=28°,即∠CDO−∠OBD=28°,
∴∠ABO=72°,∠OBD=44°,故答案为44.

5如图,在四边形ABCD中,边BC,CD的垂直平分线AE,AF恰好相交于顶点A.
(1)求证:∠BAE+∠DAF= ∠EAF.
(2)连接BD,若∠EAF= 65°,∠DBC= 40°,求∠ADC的度数.
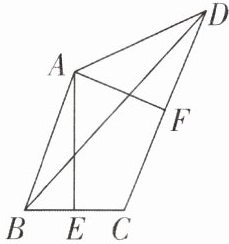
(1)求证:∠BAE+∠DAF= ∠EAF.
(2)连接BD,若∠EAF= 65°,∠DBC= 40°,求∠ADC的度数.

答案:
5.
(1)[证明]连接AC.
∵AF垂直平分CD,
∴AC=AD.在Rt△ACF和Rt△ADF中,{AC=AD,AF=AF},
∴Rt△ACF≌Rt△ADF(HL),
∴∠CAF=∠DAF;同理可证Rt△ABE≌Rt△ACE,
∴∠BAE=∠CAE,
∴∠BAE+∠DAF=∠CAE+∠CAF=∠EAF.
(2)[解]过点A作AG⊥BD于点G;由
(1)得,∠BAE+∠DAF=∠EAF=65°,
∴∠BAD=2∠EAF=130°.又
∵直线AE,AF分别是边BC,CD的垂直平分线,
∴∠AEC=∠AFC=90°,
∴∠ECF=360°−∠EAF−∠AEC−∠AFC=360°−245°=115°.
∵∠DBC=40°,
∴∠BDC=180°−115°−40°=25°.
∵∠BAD=130°,
∴∠ABD+∠ADB=50°.在Rt△ABG和Rt△ADG中,{AB=AD,AG=AG},
∴Rt△ABG≌Rt△ADG (HL),
∴∠ABG=∠ADG,
∴∠ADG=25°,
∴∠ADC=∠ADB+∠BDC=25°+25°=50°.
(1)[证明]连接AC.
∵AF垂直平分CD,
∴AC=AD.在Rt△ACF和Rt△ADF中,{AC=AD,AF=AF},
∴Rt△ACF≌Rt△ADF(HL),
∴∠CAF=∠DAF;同理可证Rt△ABE≌Rt△ACE,
∴∠BAE=∠CAE,
∴∠BAE+∠DAF=∠CAE+∠CAF=∠EAF.
(2)[解]过点A作AG⊥BD于点G;由
(1)得,∠BAE+∠DAF=∠EAF=65°,
∴∠BAD=2∠EAF=130°.又
∵直线AE,AF分别是边BC,CD的垂直平分线,
∴∠AEC=∠AFC=90°,
∴∠ECF=360°−∠EAF−∠AEC−∠AFC=360°−245°=115°.
∵∠DBC=40°,
∴∠BDC=180°−115°−40°=25°.
∵∠BAD=130°,
∴∠ABD+∠ADB=50°.在Rt△ABG和Rt△ADG中,{AB=AD,AG=AG},
∴Rt△ABG≌Rt△ADG (HL),
∴∠ABG=∠ADG,
∴∠ADG=25°,
∴∠ADC=∠ADB+∠BDC=25°+25°=50°.
6[2025江苏盐城射阳调研]如图,在△ABC中,已知点D在BC上,且BD+AD= BC,则点D在(

A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点处
D.AB的垂直平分线上
A
)
A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点处
D.AB的垂直平分线上
答案:
6.A [解析]
∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,故选A.
∵BD+DC=BC,BD+AD=BC,
∴DC=DA,
∴点D在AC的垂直平分线上,故选A.
7[2025山东滨州质检]如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,下列结论中不一定成立的是(

A.PA= PB
B.AB垂直平分OP
C.OA= OB
D.PO平分∠APB
B
)
A.PA= PB
B.AB垂直平分OP
C.OA= OB
D.PO平分∠APB
答案:
7.B [解析]
∵OP平分∠AOB,
∴∠POA=∠POB.在△APO与△BPO中,{∠POA=∠POB,∠PAO=∠PBO=90°,OP=OP},
∴△APO≌△BPO(AAS),
∴PA=PB,OA=OB,∠APO=∠BPO,即PO平分∠APB,故A、C、D不符合题意.AB不一定垂直平分OP,故B符合题意,故选B.
∵OP平分∠AOB,
∴∠POA=∠POB.在△APO与△BPO中,{∠POA=∠POB,∠PAO=∠PBO=90°,OP=OP},
∴△APO≌△BPO(AAS),
∴PA=PB,OA=OB,∠APO=∠BPO,即PO平分∠APB,故A、C、D不符合题意.AB不一定垂直平分OP,故B符合题意,故选B.
8如图,Rt△ABC中,∠ACB= 90°,D是AB上一点,BD= BC,过点D作AB的垂线交AC于点E,连接BE交CD于点F,求证:BE垂直平分CD.
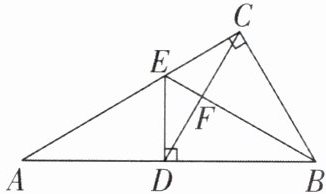

答案:
8.[证明]
∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中,{BE=BE,BD=BC},
∴Rt△BDE≌Rt△BCE(HL),
∴ED=EC.又
∵BD=BC,
∴BE垂直平分CD.
∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中,{BE=BE,BD=BC},
∴Rt△BDE≌Rt△BCE(HL),
∴ED=EC.又
∵BD=BC,
∴BE垂直平分CD.
9[2024江苏无锡调研]如图,在△ABC中,AD是BC边上的高,在线段DC上取一点E,使BD= DE,已知AB+BD= DC,求证:E点在线段AC的垂直平分线上.
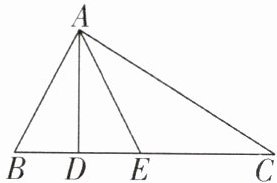

答案:
9.[证明]
∵AD是BC边上的高,
∴AD⊥BC.又
∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE.又
∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE,
∴EC=AE,
∴点E在线段AC的垂直平分线上.
∵AD是BC边上的高,
∴AD⊥BC.又
∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE.又
∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE,
∴EC=AE,
∴点E在线段AC的垂直平分线上.
查看更多完整答案,请扫码查看


