第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
11 [2025山东青岛期末]在直角三角形纸片ABC中,∠A= 90°,折叠纸片使得点A落在BC边上点D处,折痕是BE(如图(1)).将纸片复原,再次折叠纸片,使得点B落在边AC上的点E处,折痕是MN(如图(2)).若AB= 6,AC= 8,则CN的长为____
$\frac{25}{4}$
.
答案:
$\frac{25}{4}$【解析】
∵AB = 6,AC = 8,∠A = 90°,
∴$BC = \sqrt{AB² + AC²}$ = 10.如题图
(1),
∵折叠纸片使得点A落在BC边上点D处,折痕是BE,
∴AB = BD = 6,AE = DE,∠BDE = ∠A = 90°,∠ABE = ∠CBE,
∴∠CDE = 90°,CD = BC - BD = 4,
∴DE² + CD² = CE²,
∴AE² + 4² = (8 - AE)²,
∴AE = 3.如题图
(2),
∵折叠纸片,使得点B落在边AC上的点E处,折痕是MN,
∴BN = EN,
∴∠NBE = ∠NEB.
∵∠ABE = ∠CBE,
∴∠ABE = ∠NEB,
∴EN//AB,
∴∠CEN = ∠A = 90°,
∴CN² = NE² + CE²,
∴CN² = (10 - CN)² + (8 - 3)²,
∴$CN = \frac{25}{4}$,故答案为$\frac{25}{4}$.
∵AB = 6,AC = 8,∠A = 90°,
∴$BC = \sqrt{AB² + AC²}$ = 10.如题图
(1),
∵折叠纸片使得点A落在BC边上点D处,折痕是BE,
∴AB = BD = 6,AE = DE,∠BDE = ∠A = 90°,∠ABE = ∠CBE,
∴∠CDE = 90°,CD = BC - BD = 4,
∴DE² + CD² = CE²,
∴AE² + 4² = (8 - AE)²,
∴AE = 3.如题图
(2),
∵折叠纸片,使得点B落在边AC上的点E处,折痕是MN,
∴BN = EN,
∴∠NBE = ∠NEB.
∵∠ABE = ∠CBE,
∴∠ABE = ∠NEB,
∴EN//AB,
∴∠CEN = ∠A = 90°,
∴CN² = NE² + CE²,
∴CN² = (10 - CN)² + (8 - 3)²,
∴$CN = \frac{25}{4}$,故答案为$\frac{25}{4}$.
12 [2025江苏宿迁质检]如图,△ABC是等边三角形,AB= 2cm,求高AD的长和△ABC的面积.

答案:
【解】
∵△ABC是等边三角形,AD是△ABC的高,AB = 2cm,
∴BC = AB = 2cm,
∴$BD = \frac{1}{2}BC = 1$cm,
∴$AD = \sqrt{AB² - BD²} = \sqrt{3}$cm,
∴△ABC的面积 = $\frac{1}{2}BC·AD = \frac{1}{2}×2×\sqrt{3} = \sqrt{3}$(cm²).
∵△ABC是等边三角形,AD是△ABC的高,AB = 2cm,
∴BC = AB = 2cm,
∴$BD = \frac{1}{2}BC = 1$cm,
∴$AD = \sqrt{AB² - BD²} = \sqrt{3}$cm,
∴△ABC的面积 = $\frac{1}{2}BC·AD = \frac{1}{2}×2×\sqrt{3} = \sqrt{3}$(cm²).
13 如图,在△ABC中,AB= AC.
(1)若P为BC的中点,求证:$AB^2 - AP^2 = BP·CP.$
(2)若P为BC上的任意一点,(1)中的结论是否还成立?请说明理由.
(3)若P为BC延长线上一点,说明AB,AP,BP,CP之间的数量关系.

(1)若P为BC的中点,求证:$AB^2 - AP^2 = BP·CP.$
(2)若P为BC上的任意一点,(1)中的结论是否还成立?请说明理由.
(3)若P为BC延长线上一点,说明AB,AP,BP,CP之间的数量关系.

答案:
(1)【证明】如图
(1)所示,连接AP.
∵AB = AC,P是BC中点,
∴AP⊥BC,BP = CP.在Rt△ABP中,AB² = BP² + AP²,
∴AB² - AP² = BP².又
∵BP = CP,
∴BP·CP = BP²,
∴AB² - AP² = BP·CP.

【解】
(2)成立.理由:如图
(2)所示,连接AP,作AD⊥BC交BC于D.
∵AB = AC,AD⊥BC,
∴BD = CD.在Rt△ABD中,AB² = AD² + BD².同理,AP² = AD² + DP²,
∴AB² - AP² = AD² + BD² - (AD² + DP²) = BD² - DP².又
∵BP = BD + DP,CP = CD - DP = BD - DP,
∴BP·CP = (BD + DP)(BD - DP) = BD² - DP²,
∴AB² - AP² = BP·CP.

(3)AP² - AB² = BP·CP.如图
(3),P是BC延长线上任意一点,连接AP,并作AD⊥BC交BC于D.
∵AB = AC,AD⊥BC,
∴BD = CD.在Rt△ABD中,AB² = AD² + BD²,在Rt△ADP中,AP² = AD² + DP²,
∴AP² - AB² = (AD² + PD²) - (AD² + DB²) = PD² - BD²,又
∵BP = BD + DP,CP = DP - CD = DP - BD,
∴BP·CP = (BD + DP)(DP - BD) = DP² - BD²,
∴AP² - AB² = BP·CP.

(1)【证明】如图
(1)所示,连接AP.
∵AB = AC,P是BC中点,
∴AP⊥BC,BP = CP.在Rt△ABP中,AB² = BP² + AP²,
∴AB² - AP² = BP².又
∵BP = CP,
∴BP·CP = BP²,
∴AB² - AP² = BP·CP.

【解】
(2)成立.理由:如图
(2)所示,连接AP,作AD⊥BC交BC于D.
∵AB = AC,AD⊥BC,
∴BD = CD.在Rt△ABD中,AB² = AD² + BD².同理,AP² = AD² + DP²,
∴AB² - AP² = AD² + BD² - (AD² + DP²) = BD² - DP².又
∵BP = BD + DP,CP = CD - DP = BD - DP,
∴BP·CP = (BD + DP)(BD - DP) = BD² - DP²,
∴AB² - AP² = BP·CP.

(3)AP² - AB² = BP·CP.如图
(3),P是BC延长线上任意一点,连接AP,并作AD⊥BC交BC于D.
∵AB = AC,AD⊥BC,
∴BD = CD.在Rt△ABD中,AB² = AD² + BD²,在Rt△ADP中,AP² = AD² + DP²,
∴AP² - AB² = (AD² + PD²) - (AD² + DB²) = PD² - BD²,又
∵BP = BD + DP,CP = DP - CD = DP - BD,
∴BP·CP = (BD + DP)(DP - BD) = DP² - BD²,
∴AP² - AB² = BP·CP.

14 [2025广东佛山期中]综合运用:
“在△ABC中,AB,BC,AC三边的长分别为$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$,求这个三角形的面积.”小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图(1)所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫作构图法.
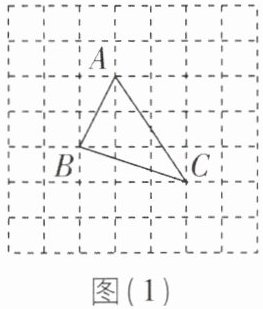


(1)直接运用:
①请直接写出图(1)中△ABC的面积:____.
②请在图(2)中画出一个面积为10且顶点都在格点上的等腰直角三角形.
(2)变式应用:若△MNP的边长分别为MN = $\sqrt{m^2 + 16n^2}$,PN = $\sqrt{9m^2 + 4n^2}$,PM = $\sqrt{4m^2 + 4n^2}$(n > m > 0,且m ≠ n),试运用构图法在图(3)中(已标注m,n的长度)画出相应的△MNP,并用m,n表示△MNP的面积.
(3)拓展应用:求代数式$\sqrt{x^2 + 1} + \sqrt{(4 - x)^2 + 4}$(0 ≤ x ≤ 4)的最小值.
“在△ABC中,AB,BC,AC三边的长分别为$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$,求这个三角形的面积.”小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图(1)所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫作构图法.



(1)直接运用:
①请直接写出图(1)中△ABC的面积:____.
②请在图(2)中画出一个面积为10且顶点都在格点上的等腰直角三角形.
(2)变式应用:若△MNP的边长分别为MN = $\sqrt{m^2 + 16n^2}$,PN = $\sqrt{9m^2 + 4n^2}$,PM = $\sqrt{4m^2 + 4n^2}$(n > m > 0,且m ≠ n),试运用构图法在图(3)中(已标注m,n的长度)画出相应的△MNP,并用m,n表示△MNP的面积.
(3)拓展应用:求代数式$\sqrt{x^2 + 1} + \sqrt{(4 - x)^2 + 4}$(0 ≤ x ≤ 4)的最小值.
答案:
【解】
(1)①由网格可得S△ABC = 3×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3 = $\frac{7}{2}$,故答案为$\frac{7}{2}$.
②如图
(1),△DEF即为所求.

(2)如图
(2),△MNP即为所求.

△MNP的面积 = 3m×4n - $\frac{1}{2}$×m×4n - $\frac{1}{2}$×2m×2n - $\frac{1}{2}$×3m×2n = 12mn - 2mn - 2mn - 3mn = 5mn.
(3)构造图形如图
(3),其中四边形CDBE为长方形,点P为CD上一点,点A在射线EC上,AC = 1,DB = 2,CD = 4,CP = x,PD = 4 - x,
∴$AP + BP = \sqrt{x² + 1} + \sqrt{(4 - x)² + 4}$(0 ≤ x ≤ 4),连接AB,交CD于点F,则AP + BP的最小值为AB的长.
∵AE = AC + CE = 1 + 2 = 3,BE = CD = 4,
∴由勾股定理,得AB = $\sqrt{AE² + BE²} = \sqrt{3² + 4²} = 5$,
∴代数式$\sqrt{x² + 1} + \sqrt{(4 - x)² + 4}$(0 ≤ x ≤ 4)的最小值是5.

【解】
(1)①由网格可得S△ABC = 3×3 - $\frac{1}{2}$×1×3 - $\frac{1}{2}$×1×2 - $\frac{1}{2}$×2×3 = $\frac{7}{2}$,故答案为$\frac{7}{2}$.
②如图
(1),△DEF即为所求.

(2)如图
(2),△MNP即为所求.

△MNP的面积 = 3m×4n - $\frac{1}{2}$×m×4n - $\frac{1}{2}$×2m×2n - $\frac{1}{2}$×3m×2n = 12mn - 2mn - 2mn - 3mn = 5mn.
(3)构造图形如图
(3),其中四边形CDBE为长方形,点P为CD上一点,点A在射线EC上,AC = 1,DB = 2,CD = 4,CP = x,PD = 4 - x,
∴$AP + BP = \sqrt{x² + 1} + \sqrt{(4 - x)² + 4}$(0 ≤ x ≤ 4),连接AB,交CD于点F,则AP + BP的最小值为AB的长.
∵AE = AC + CE = 1 + 2 = 3,BE = CD = 4,
∴由勾股定理,得AB = $\sqrt{AE² + BE²} = \sqrt{3² + 4²} = 5$,
∴代数式$\sqrt{x² + 1} + \sqrt{(4 - x)² + 4}$(0 ≤ x ≤ 4)的最小值是5.

查看更多完整答案,请扫码查看


