《2025年初中必刷题八年级数学上册苏科版》

比较$2,\sqrt {5},\sqrt [3]{7}$的大小,正确的是 (C)
A.$\sqrt {5}＜\sqrt [3]{7}＜2$
B.$2＜\sqrt [3]{7}＜\sqrt {5}$
C.$\sqrt [3]{7}＜2＜\sqrt {5}$
D.$2＜\sqrt {5}＜\sqrt [3]{7}$

答案： C [解析]因为$2^{2}=4$,$(\sqrt{5})^{2}=5$,$4＜5$,所以$2＜\sqrt{5}$.因为$2^{3}=8$,$(\sqrt[3]{7})^{3}=7$,$7＜8$,所以$\sqrt[3]{7}＜2$,所以$\sqrt[3]{7}＜2＜\sqrt{5}$.故选C.

(1)$-\frac {1}{2}$＞$-\frac {\sqrt {3}}{2}$; (2)3＞$\sqrt [3]{9}$.

答案：
(1)＞
(2)＞ [解析]
(1)因为$1＜3$,所以$1＜\sqrt{3}$,所以$\frac{1}{2}＜\frac{\sqrt{3}}{2}$,所以$-\frac{1}{2}＞-\frac{\sqrt{3}}{2}$,故答案为＞.
(2)因为$3=\sqrt[3]{27}$,$27＞9$,所以$\sqrt[3]{27}＞\sqrt[3]{9}$,所以$3＞\sqrt[3]{9}$,故答案为＞.

3 [中]如图,点A是数轴上表示实数a的点.
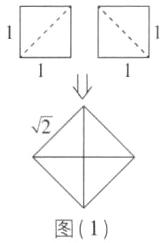
(1)用直尺和圆规在数轴上作出表示实数$\sqrt {2}$的点P.(保留作图痕迹,不写作法)
(2)利用数轴比较$\sqrt {2}$和a的大小,并说明理由.

答案：
[解]
(1)如图
(1)、图
(2)所示,点P即为所求
(2)$a＞\sqrt{2}$.理由如下:如图
(2)所示，由
(1)知点P表示的数为$\sqrt{2}$,因为点A在点P右侧，所以$a＞\sqrt{2}$

(1)比较大小:$3+\sqrt {5}$＜$\sqrt {10}+\sqrt {5}$.(填“＜”“=”或“＞”)
(2)已知$2y-2= x$,且$x≥0$,若$A= 5xy+y+1,B= 5xy+2y$,试比较A和B的大小.
因为$x=2y-2$,$x\geq0$,所以$2y-2\geq0$,所以$y-1\geq0$,所以$-y+1\leq0$,所以$A-B=(5xy+y+1)-(5xy+2y)=-y+1\leq0$,所以$A\leq B$.

答案： [解]
(1)$3+\sqrt{5}-(\sqrt{10}+\sqrt{5})=3+\sqrt{5}-\sqrt{10}-\sqrt{5}=3-\sqrt{10}$.因为$3-\sqrt{10}＜0$,所以$3+\sqrt{5}-(\sqrt{10}+\sqrt{5})＜0$,所以$3+\sqrt{5}＜\sqrt{10}+\sqrt{5}$.故答案为＜.
(2)因为$x=2y-2$,$x\geq0$,所以$2y-2\geq0$,所以$y-1\geq0$,所以$-y+1\leq0$,所以$A-B=(5xy+y+1)-(5xy+2y)=-y+1\leq0$,所以$A\leq B$.

5 [2024江苏南京期末,中]已知$a= 5+\sqrt {5},b= 3+\sqrt {10},c= \sqrt {30}$,通过估算,比较a,b,c的大小.

答案： [解]
∵$4＜5＜9$,
∴$2＜\sqrt{5}＜3$,
∴$7＜5+\sqrt{5}＜8$,即$7＜a＜8$.
∵$9＜10＜16$,
∴$3＜\sqrt{10}＜4$,
∴$6＜3+\sqrt{10}＜7$,即$6＜b＜7$.
∵$25＜30＜36$,
∴$5＜\sqrt{30}＜6$,即$5＜c＜6$.
∴$a,b,c$的大小关系为$c＜b＜a$.

6 [难]观察下列一组等式,再解答问题:
$(\sqrt {2}+1)(\sqrt {2}-1)= 1,(\sqrt {3}+\sqrt {2})(\sqrt {3}-\sqrt {2})= 1,$
$(\sqrt {4}+\sqrt {3})(\sqrt {4}-\sqrt {3})= 1,(\sqrt {5}+\sqrt {4})(\sqrt {5}-\sqrt {4})= 1,… .$
(1)利用上面的规律,计算下列式子的值.
$(\frac {1}{\sqrt {2}+1}+\frac {1}{\sqrt {3}+\sqrt {2}}+\frac {1}{\sqrt {4}+\sqrt {3}}+… +\frac {1}{\sqrt {2022}+\sqrt {2021}})× (\sqrt {2022}+1).$
(2)利用上面的规律,比较$\sqrt {11}-\sqrt {10}与\sqrt {12}-\sqrt {11}$的大小.

答案： [解]
(1)由规律易知$\frac{1}{\sqrt{n + 1}+\sqrt{n}}=\sqrt{n + 1}-\sqrt{n}$($n$为正整数).
原式$=[(\sqrt{2}-1)+(\sqrt{3}-\sqrt{2})+(\sqrt{4}-\sqrt{3})+\cdots+(\sqrt{2022}-\sqrt{2021})]×(\sqrt{2022}+1)$
$=(\sqrt{2022}-1)×(\sqrt{2022}+1)$
$=2021$.
(2)因为$\frac{1}{\sqrt{11}-\sqrt{10}}=\sqrt{11}+\sqrt{10}$,$\frac{1}{\sqrt{12}-\sqrt{11}}=\sqrt{12}+\sqrt{11}$,且$\sqrt{11}+\sqrt{10}＜\sqrt{12}+\sqrt{11}$,所以$\frac{1}{\sqrt{11}-\sqrt{10}}＜\frac{1}{\sqrt{12}-\sqrt{11}}$,所以$\sqrt{11}-\sqrt{10}＞\sqrt{12}-\sqrt{11}$.