《2025年初中必刷题八年级数学上册苏科版》

1 [2024四川内江中考]16的平方根是 (D)
A.-4
B.4
C.2
D.±4

答案： D [解析]16 的平方根是±4,故选 D.

2 [2024广东中考]完全相同的4个正方形面积之和是100,则正方形的边长是 (B)
A.2
B.5
C.10
D.20

答案： B [解析]
∵完全相同的 4 个正方形面积之和是 100,
∴1 个正方形的面积为 100÷4=25,
∴正方形的边长为 $\sqrt{25}$=5，故选 B.

3 [2024四川成都中考]若m,n为实数,且$(m + 4)^2+\sqrt{n - 5}= 0$,则$(m + n)^2$的值为______1.

答案： 1 [解析]
∵m,n 为实数,且(m+4)²+$\sqrt{n - 5}$=0,
∴m+4=0,n - 5=0,解得 m=-4,n=5,
∴(m+n)²=(-4+5)²=1²=1. 故答案为 1.

已知$a= \sqrt{5}$,$b = 2$,$c= \sqrt{3}$,则a,b,c的大小关系是 (C)
A.$b ＞ a ＞ c$
B.$a ＞ c ＞ b$
C.$a ＞ b ＞ c$
D.$b ＞ c ＞ a$

答案： C [解析]
∵3＜4＜5,
∴$\sqrt{3}$＜$\sqrt{4}$＜$\sqrt{5}$,
∴$\sqrt{3}$＜2＜$\sqrt{5}$,即 a＞b＞c,故选 C.

5 [四川绵阳中考]正整数a,b分别满足$\sqrt[3]{53}＜a＜\sqrt[3]{98}$,$\sqrt{2}＜b＜\sqrt{7}$,则$b^a= $ (D)
A.4
B.8
C.9
D.16

答案： D [解析]
∵$\sqrt[3]{53}$＜$\sqrt[3]{64}$＜$\sqrt[3]{98}$,$\sqrt{2}$＜$\sqrt{4}$＜$\sqrt{7}$,
∴a=4,b=2,
∴bᵃ=2⁴=16. 故选 D.

6 [2024天津中考]估计$\sqrt{10}$的值在 (C)
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间

答案： C [解析]
∵$\sqrt{9}$＜$\sqrt{10}$＜$\sqrt{16}$,
∴3＜$\sqrt{10}$＜4,
∴$\sqrt{10}$的值在 3 和 4 之间. 故选 C.

7 [2024四川资阳中考]若$\sqrt{5}＜m＜\sqrt{10}$,则整数m的值为 (B)
A.2
B.3
C.4
D.5

答案： B [解析]
∵$\sqrt{4}$＜$\sqrt{5}$＜$\sqrt{9}$,
∴2＜$\sqrt{5}$＜3.
∵$\sqrt{9}$＜$\sqrt{10}$＜$\sqrt{16}$,
∴3＜$\sqrt{10}$＜4. 又
∵$\sqrt{5}$＜m＜$\sqrt{10}$,
∴整数 m 的值为 3,故选 B.

8 [2024广东深圳中考]如图所示,四边形ABCD,DEFG,GHIJ均为正方形,且$S_{正方形ABCD}= 10$,$S_{正方形GHIJ}= 1$,则正方形DEFG的边长可以是 ______.(写出一个答案即可)


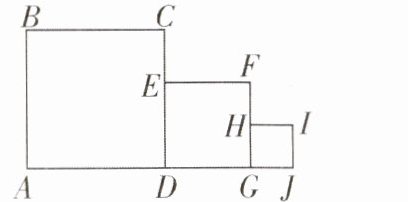
2

答案： 2(答案不唯一) [解析]
∵S_正方形ABCD=10,
∴AB=CD=$\sqrt{10}$.
∵S_正方形GHIJ=1,
∴GH=GJ=1.
∵3＜$\sqrt{10}$＜4,即 3＜CD＜4,正方形 DEFG 的边长满足 GH＜DE＜CD,
∴正方形 DEFG 的边长可以是 2,故答案为 2(答案不唯一).

9 [2024山东日照中考]计算:$|\sqrt{2}-2|+\sqrt{2}-2024^0= $1.

答案： 1 [解析]|$\sqrt{2}$ - 2|+$\sqrt{2}$ - 2024⁰=2 - $\sqrt{2}$+$\sqrt{2}$ - 1=1,故答案为 1.

10 [2023湖北仙桃中考]计算$4^{-1}-\sqrt{\frac{1}{16}}+(3-\sqrt{2})^0$的结果是1.

答案： 1 [解析]4⁻¹ - $\sqrt{\frac{1}{16}}$+(3 - $\sqrt{2}$)⁰=$\frac{1}{4}$ - $\frac{1}{4}$+1=1. 故答案为 1.

11 [2024广东中考]计算:$2^0×|-\frac{1}{3}|+\sqrt{4}-3^{-1}$.

答案： 【解】原式=1×$\frac{1}{3}$+2 - $\frac{1}{3}$=$\frac{1}{3}$+2 - $\frac{1}{3}$=2.

12 [2024吉林中考]先化简,再求值:$(a + 1)(a - 1)+a^2 + 1$,其中$a= \sqrt{3}$.

答案： 【解】(a+1)(a - 1)+a²+1=a² - 1+a²+1=2a².
∵a=$\sqrt{3}$,
∴原式=2×($\sqrt{3}$)²=6.

13 [2024四川南充中考]如图,数轴上表示$\sqrt{2}$的点是 (C)

A.点A
B.点B
C.点C
D.点D

答案： C [解析]
∵$\sqrt{1}$＜$\sqrt{2}$＜$\sqrt{4}$,
∴1＜$\sqrt{2}$＜2. 由数轴可知,只有点 C 表示的数在 1 和 2 之间,故选 C.

14 [内蒙古赤峰中考]实数a,b,c在数轴上对应点的位置如图所示.如果$a + b = 0$,那么下列结论正确的是 (C)

A.$|a|＞|c|$
B.$a + c ＜ 0$
C.$abc ＜ 0$
D.$\frac{a}{b}= 1$

答案： C [解析]
∵a+b=0,
∴a,b 互为相反数,
∴a 所对应的点到原点的距离小于 c 所对应的点到原点的距离,
∴|a|＜|c|,a+c＞0,故 A 选项错误,B 选项错误;
∵a＜0＜b＜c,
∴abc＜0,故 C 选项正确;
∵a+b=0,
∴a,b 互为相反数,
∴$\frac{a}{b}$=-1,故 D 选项错误. 故选 C.