《2025年初中必刷题八年级数学上册苏科版》

1 [中]如图,已知AC,BD相交于点O,且AB= DC,AC= DB,那么∠A= ∠D吗？说明理由。

答案：
【解】∠A=∠D。理由如下：
如图，连接BC。在△ABC和△DCB中，
AB=DC，
{AC=DB，
BC=CB，
∴△ABC≌△DCB(SSS)，
∴∠A=∠D。

2 [中]如图,△AOB中,OA= OB,∠AOB= 90°,BD平分∠ABO交OA于D,AE⊥BD交BD的延长线于E。求证：BD= 2AE。

答案：
【证明】如图，延长BO，AE交于F。
∵BD平分∠ABO，AF⊥BD，
∴∠1=∠2，∠AEB=∠FEB=90°。
在△ABE和△FBE中，{∠1=∠2，
BE=BE，
∠AEB=∠FEB，
思路分析：延长BO，AE交于F，先证△ABE≌△FBE，推出AE=EF，再证△OBD≌△OAF，推出BD=AF，进而即可得证。
关键点拨：本题主要考查了全等三角形的判定及性质，平行线的性质，角平分线的定义，正确作出辅助线是解题的关键。
∴△ABE≌△FBE(ASA)，
∴AE=EF。
∵∠AOB=90°，∠AED=90°，∠ADE=∠BDO，
∴∠2=∠OAF。
∵∠AOB=90°，
∴∠DOB=∠FOA=90°。
在△OBD和△OAF中，{∠2=∠FAO，
BO=AO，
∠BOD=∠AOF，
∴△OBD≌△OAF(ASA)，
∴BD=AF。
∵AE=EF，
∴BD=2AE。

3 [中]如图,在四边形ABCD中,AB//CD,E是边AD上的点,BE平分∠ABC,CE平分∠BCD。求证：(1)BE⊥CE；(2)BC= AB+CD。

答案：
【证明】
(1)
∵AB//CD，
∴∠ABC+∠DCB=180°。
∵BE平分∠ABC，CE平分∠BCD，
∴∠EBC=1/2∠ABC，∠ECB=1/2∠BCD，
∴∠EBC+∠ECB=1/2(∠ABC+∠BCD)=90°，
∴∠BEC=180°-(∠EBC+∠ECB)=180°-90°=90°，
∴BE⊥CE。
(2)如图，在BC上截取BF=AB，连接EF。
∵BE平分∠ABC，
∴∠ABE=∠FBE。
在△BAE和△BFE中，{BA=BF，
∠ABE=∠FBE，
BE=BE，
∴△BAE≌△BFE(SAS)，
∴∠BEA=∠BEF。
∵BE⊥CE，
∴∠BEF+∠CEF=∠AEB+∠DEC=90°，
∴∠FEC=∠DEC。
∵CE平分∠BCD，
∴∠ECF=∠ECD。
在△CFE和△CDE中，{∠FEC=∠DEC，
CE=CE，
∠ECF=∠ECD，
∴△CFE≌△CDE(ASA)，
∴CF=CD，
∴BC=BF+CF=AB+CD。

4 [中]如图,AD是△ABC的中线,点E在BC的延长线上,CE= AB,∠BAC= ∠BCA,求证：AE= 2AD。

答案：
【证明】如图，延长AD至M，使DM=AD，连接CM。因为AD是△ABC的中线，所以BD=CD。
在△ABD和△MCD中，{BD=CD，
∠ADB=∠MDC，
AD=MD，
所以△ABD≌△MCD(SAS)，所以MC=AB，∠B=∠MCD。因为AB=CE，所以CM=CE。因为∠BAC=∠BCA，所以∠B+∠BAC=∠ACB+∠MCD，即∠ACE=∠ACM。
在△ACE和△ACM中，{AC=AC，
∠ACE=∠ACM，
CE=CM，
所以△ACE≌△ACM(SAS)，所以AE=AM。因为AM=2AD，所以AE=2AD。

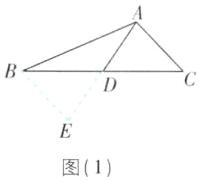
5 [2025江苏南京质检,较难](1)如图(1),在△ABC中,AB= 9,AC= 5,求BC边上的中线AD的取值范围。
(2)如图(2),AD是△ABC的中线,AB= AE,AC= AF,∠BAE= ∠FAC= 90°,试探究线段AD与EF的数量和位置关系,并加以证明。

答案：
【解】
(1)如图
(1)，延长AD到E，使得AD=DE，则AE=2AD。
∵D是BC的中点，
∴BD=CD。在△ACD和△EBD中，{CD=BD，
∠ADC=∠EDB，
AD=DE，
∴△ACD≌△EBD(SAS)，
∴BE=AC。在△ABE中，由三角形的三边关系可得AB - BE＜AE＜AB + BE，即AB - BE＜2AD＜AB + BE。
∵AB=9，AC=BE=5，
∴9 - 5＜2AD＜9 + 5，
∴2＜AD＜7，
∴BC边上的中线AD的取值范围为2＜AD＜7。

(2)EF=2AD且EF⊥AD。证明如下：如图
(2)，延长AD到G，使得AD=DG，延长DA交EF于点H。同
(1)可证△ACD≌△GBD，
∴AC=BG，∠DAC=∠DGB，
∴∠BAC=∠BAD+∠DAC=∠BAD+∠DGB，
∴∠ABG+∠BAD+∠DGB=∠ABG+∠BAC=180°。
∵∠BAE=∠FAC=90°，
∴∠EAF+∠BAC=180°，
∴∠EAF=∠ABG。
∵AC=AF，AC=BG，
∴BG=AF。在△ABG和△EAF中，{AB=AE，
∠ABG=∠EAF，
BG=AF，
∴△ABG≌△EAF(SAS)，
∴EF=AG，∠HEA=∠BAG。
∵AG=2AD，
∴EF=2AD。
∵∠BAE=90°，
∴∠EAH+∠BAG=90°。
∵∠HEA=∠BAG，
∴∠HEA+∠EAH=90°，
∴∠AHE=90°，
∴AD⊥EF。综上所述，EF=2AD且EF⊥AD。