第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2024 江苏苏州工业园区期末]如图,已知$∠BAC= ∠DCA$。若添加一个条件后,可得$△ABC\cong △CDA$,则在下列条件中,不能添加的是(
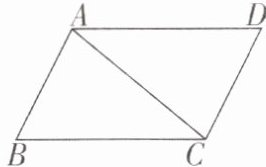
A.$AB= CD$
B.$∠B= ∠D$
C.$BC// AD$
D.$BC= DA$
D
)
A.$AB= CD$
B.$∠B= ∠D$
C.$BC// AD$
D.$BC= DA$
答案:
D 【解析】
∵ AB = CD,∠BAC = ∠ACD,AC = CA,
∴ △ABC≌△CDA(SAS),
∴ 选项 A 不符合题意
∵ ∠B = ∠D,∠BAC = ∠ACD,AC = CA,
∴ △ABC≌△CDA(AAS),
∴ 选项 B 不符合题意
∵ BC//AD,
∴ ∠ACB = ∠CAD.
∵ ∠BAC = ∠ACD,AC = CA,
∴ △ABC ≌ △CDA(ASA),
∴ 选项 C 不符合题意
添加 BC = DA 不能判定△ABC≌△CDA,
∴ 选项 D 符合题意
∵ AB = CD,∠BAC = ∠ACD,AC = CA,
∴ △ABC≌△CDA(SAS),
∴ 选项 A 不符合题意
∵ ∠B = ∠D,∠BAC = ∠ACD,AC = CA,
∴ △ABC≌△CDA(AAS),
∴ 选项 B 不符合题意
∵ BC//AD,
∴ ∠ACB = ∠CAD.
∵ ∠BAC = ∠ACD,AC = CA,
∴ △ABC ≌ △CDA(ASA),
∴ 选项 C 不符合题意
添加 BC = DA 不能判定△ABC≌△CDA,
∴ 选项 D 符合题意
2 已知$△ABC$如图所示,则甲、乙、丙三个三角形中与$△ABC$全等的是(
A.甲、乙
B.乙、丙
C.只有乙
D.只有丙
B
)A.甲、乙
B.乙、丙
C.只有乙
D.只有丙
答案:
B 【解析】已知△ABC 中,∠B = 50°,∠C = 58°,∠A = 72°,BC = a,AB = c,AC = b. 甲:只有一条边和 AB 相等,没有其他条件,不符合三角形全等的判定定理,故与△ABC 不一定全等;乙:有两个角对应相等,其中一角的对边相等,符合三角形全等的判定定理“AAS”,故与△ABC 全等;丙:符合“SAS”判定定理,故与△ABC 全等. 故选 B.
3 [2024 江苏南京建邺区期中]已知:如图,线段$AC$,$BD相交于点O$,分别连接$AB$,$CD$,$BC$,则$△ABC\cong △DCB$。求证:$△ABO\cong △DCO$。
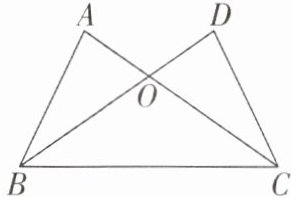

答案:
【证明】
∵ △ABC≌△DCB,
∴ AB = DC,∠A = ∠D. 在△ABO 与△DCO 中,{∠A = ∠D,∠AOB = ∠DOC,AB = DC},
∴ △ABO≌△DCO(AAS).
∵ △ABC≌△DCB,
∴ AB = DC,∠A = ∠D. 在△ABO 与△DCO 中,{∠A = ∠D,∠AOB = ∠DOC,AB = DC},
∴ △ABO≌△DCO(AAS).
如图,龙龙用长方体积木垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一块三角板($AC= BC$,$∠ACB= 90^{\circ }$),点$C在DE$上,点$A$,$B$恰好与木墙的顶端重合,$AD= 6$,$BE= 14$,则两堵木墙之间的距离$DE$的长为(
A.6
B.10
C.14
D.20
D
)A.6
B.10
C.14
D.20
答案:
D 【解析】由题意得∠ADC = ∠CEB = ∠ACB = 90°,
∴ ∠ACD + ∠BCE = ∠ACD + ∠CAD = 90°,
∴ ∠CAD = ∠BCE. 在△ACD 和△CBE 中,{∠ADC = ∠CEB,∠CAD = ∠BCE,AC = BC},
∴ △ACD ≌ △CBE(AAS),
∴ AD = CE = 6,CD = BE = 14,
∴ DE = CD + CE = 14 + 6 = 20,故选 D.
∴ ∠ACD + ∠BCE = ∠ACD + ∠CAD = 90°,
∴ ∠CAD = ∠BCE. 在△ACD 和△CBE 中,{∠ADC = ∠CEB,∠CAD = ∠BCE,AC = BC},
∴ △ACD ≌ △CBE(AAS),
∴ AD = CE = 6,CD = BE = 14,
∴ DE = CD + CE = 14 + 6 = 20,故选 D.
5 [2025 江苏南京质检]如图,地面上有一根旗杆$AO$,小明两次紧拉从顶端垂下的绳子到$OC$,$OD$的位置($OC$,$OA$,$OD$在同一平面内),测得$∠COD= 90^{\circ }$,且$C$,$D两点到OA的水平距离CE$,$DF分别为1.4m和1.8m$,则$F$,$E$两点的高度差(即$FE$的长)为______$m$。


0.4
答案:
0.4 【解析】
∵ CE⊥OA,DF⊥OA,
∴ ∠CEO = ∠OFD = 90°.
∵ ∠COD = 90°,
∴ ∠COE + ∠OCE = ∠COE + ∠DOF,
∴ ∠OCE = ∠DOF. 在△COE 与△ODF 中,{∠OCE = ∠DOF,∠OEC = ∠DFO,OC = OD},
∴ △COE≌△ODF(AAS),
∴ OF = CE = 1.4 m,OE = DF = 1.8 m,
∴ EF = OE - OF = 0.4 m. 故答案为 0.4.
∵ CE⊥OA,DF⊥OA,
∴ ∠CEO = ∠OFD = 90°.
∵ ∠COD = 90°,
∴ ∠COE + ∠OCE = ∠COE + ∠DOF,
∴ ∠OCE = ∠DOF. 在△COE 与△ODF 中,{∠OCE = ∠DOF,∠OEC = ∠DFO,OC = OD},
∴ △COE≌△ODF(AAS),
∴ OF = CE = 1.4 m,OE = DF = 1.8 m,
∴ EF = OE - OF = 0.4 m. 故答案为 0.4.
6 [2025 江苏扬州质检]如图,点$B$,$F$,$C$,$E在直线l$上($F$,$C$之间不能直接测量),点$A$,$D在直线l$异侧,测得$AB= DE$,$AB// DE$,$∠ACB= ∠DFC$。
(1)求证:$△ABC\cong △DEF$;
(2)若$BE= 10m$,$BF= 3m$,求$FC$的长度。
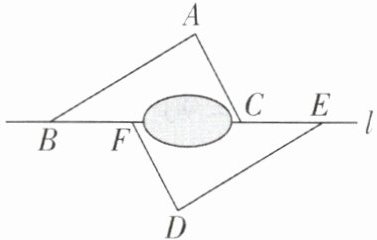
(1)求证:$△ABC\cong △DEF$;
(2)若$BE= 10m$,$BF= 3m$,求$FC$的长度。

答案:
(1)【证明】
∵ AB//DE,
∴ ∠ABC = ∠DEF. 在△ABC 与 △DEF 中,{∠ACB = ∠DFC,∠ABC = ∠DEF,AB = DE},
∴ △ABC≌△DEF(AAS).
(2)【解】
∵ △ABC ≌ △DEF,
∴ BC = EF,
∴ BF + FC = EC + FC,
∴ BF = EC.
∵ BE = 10 m,BF = 3 m,
∴ FC = 10 - 3 - 3 = 4(m).
(1)【证明】
∵ AB//DE,
∴ ∠ABC = ∠DEF. 在△ABC 与 △DEF 中,{∠ACB = ∠DFC,∠ABC = ∠DEF,AB = DE},
∴ △ABC≌△DEF(AAS).
(2)【解】
∵ △ABC ≌ △DEF,
∴ BC = EF,
∴ BF + FC = EC + FC,
∴ BF = EC.
∵ BE = 10 m,BF = 3 m,
∴ FC = 10 - 3 - 3 = 4(m).
7 如图,$E在△ABC的边AC$上,且$∠AEB= ∠ABC$。
(1)求证:$∠ABE= ∠C$。
(2)若$∠BAE的平分线AF交BE于点F$,$FD// BC交AC于点D$,$AB= 8$,$AC= 10$,求$DC$的长。
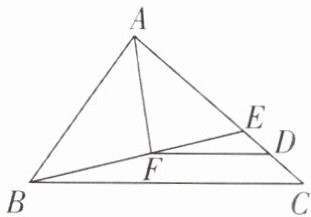
(1)求证:$∠ABE= ∠C$。
(2)若$∠BAE的平分线AF交BE于点F$,$FD// BC交AC于点D$,$AB= 8$,$AC= 10$,求$DC$的长。

答案:
(1)【证明】在△ABE 中,∠ABE = 180° - ∠BAE - ∠AEB. 在△ABC 中,∠C = 180° - ∠BAC - ∠ABC.
∵ ∠AEB = ∠ABC,∠BAE = ∠BAC,
∴ ∠ABE = ∠C.
(2)【解】
∵ FD//BC,
∴ ∠ADF = ∠C. 又
∵ ∠ABE = ∠C,
∴ ∠ABE = ∠ADF.
∵ AF 平分∠BAE,
∴ ∠BAF = ∠DAF. 在△ABF 和△ADF 中,{∠ABE = ∠ADF,∠BAF = ∠DAF,AF = AF},
∴ △ABF ≌ △ADF(AAS),
∴ AB = AD.
∵ AB = 8,AC = 10,
∴ DC = AC - AD = AC - AB = 10 - 8 = 2.
(1)【证明】在△ABE 中,∠ABE = 180° - ∠BAE - ∠AEB. 在△ABC 中,∠C = 180° - ∠BAC - ∠ABC.
∵ ∠AEB = ∠ABC,∠BAE = ∠BAC,
∴ ∠ABE = ∠C.
(2)【解】
∵ FD//BC,
∴ ∠ADF = ∠C. 又
∵ ∠ABE = ∠C,
∴ ∠ABE = ∠ADF.
∵ AF 平分∠BAE,
∴ ∠BAF = ∠DAF. 在△ABF 和△ADF 中,{∠ABE = ∠ADF,∠BAF = ∠DAF,AF = AF},
∴ △ABF ≌ △ADF(AAS),
∴ AB = AD.
∵ AB = 8,AC = 10,
∴ DC = AC - AD = AC - AB = 10 - 8 = 2.
查看更多完整答案,请扫码查看


