《2025年初中必刷题八年级数学上册苏科版》

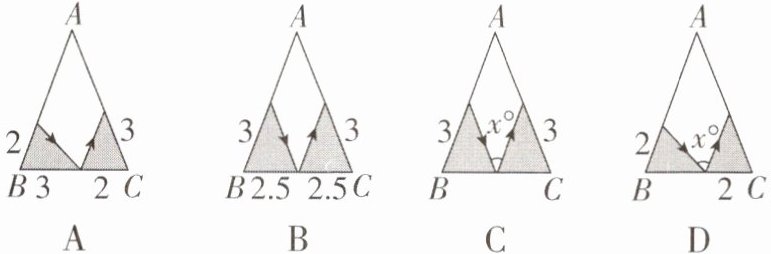
1 [中]如图,有一张三角形纸片 ABC,已知∠B= ∠C= x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )

答案：
C 【解析】A选项,由全等三角形的判定定理“SAS”证得题图中两个小三角形全等,故本选项不符合题意.B选项,由全等三角形的判定定理“SAS”证得题图中两个小三角形全等,故本选项不符合题意.C选项,如图
(1),
∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
∴BE和CF是对应边,而已知给出的是BD=FC=3,
∴不能判定两个小三角形全等,故本选项符合题意.D选项,如图
(2),
∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE.
∵BD=EC=2,∠B=∠C,
∴△BDE≌△CEF(ASA),
∴能判定两个小三角形全等,故本选项不符合题意.故选C.

如图,在△ABC 中,AB= AC,AB＞BC,点 D 在边 BC 上,CD= 2BD,点 E,F 在线段 AD 上,∠1= ∠2= ∠BAC,若△ABC 的面积为 18,则△ACF 与△BDE 的面积之和是(A)
A.6
B.8
C.9
D.12

答案： 1. 首先，利用三角形内角和定理和已知条件证明三角形全等：
因为$\angle 1=\angle BAC$，$\angle 1=\angle BAE + \angle ABE$，$\angle BAC=\angle BAE+\angle CAF$，所以$\angle ABE=\angle CAF$。
同理，因为$\angle 2=\angle BAC$，$\angle 2=\angle FCA+\angle CAF$，$\angle BAC=\angle BAE+\angle CAF$，所以$\angle BAE=\angle FCA$。
又因为$AB = AC$，在$\triangle ABE$和$\triangle CAF$中：
$\left\{\begin{array}{l}\angle ABE=\angle CAF\\AB = AC\\\angle BAE=\angle FCA\end{array}\right.$，根据$ASA$（角 - 边 - 角）定理，可得$\triangle ABE\cong\triangle CAF$。
所以$S_{\triangle ABE}=S_{\triangle CAF}$。
2. 然后，根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），求$S_{\triangle ABD}$：
已知$CD = 2BD$，设$BD=x$，则$CD = 2x$，$BC=BD + CD=3x$。
因为$\triangle ABC$和$\triangle ABD$的高相同（以$A$到$BC$的距离为高），根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），$S_{\triangle ABC}=\frac{1}{2}BC\cdot h$，$S_{\triangle ABD}=\frac{1}{2}BD\cdot h$（$h$是$A$到$BC$的距离）。
所以$\frac{S_{\triangle ABD}}{S_{\triangle ABC}}=\frac{BD}{BC}$（高相等时，三角形面积比等于底之比）。
已知$S_{\triangle ABC}=18$，$\frac{BD}{BC}=\frac{BD}{BD + CD}=\frac{1}{3}$，则$S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$。
3. 最后，求$S_{\triangle ACF}+S_{\triangle BDE}$：
因为$S_{\triangle ACF}+S_{\triangle BDE}=S_{\triangle ABE}+S_{\triangle BDE}$（$S_{\triangle ABE}=S_{\triangle CAF}$）。
而$S_{\triangle ABE}+S_{\triangle BDE}=S_{\triangle ABD}$。
又因为$S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$，$S_{\triangle ABC}=18$，所以$S_{\triangle ABD}=6$。
所以$\triangle ACF$与$\triangle BDE$的面积之和是$6$，答案是A。

3 [2024 江苏苏州昆山调研,较难]如图,在△ABC 中,∠BCA= 90°,AC= BC,AE 平分∠BAC,BE⊥AE,且 BE= 2,则△ABD 的面积是______.

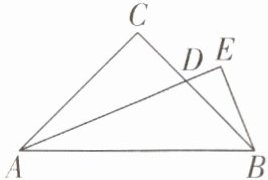
答案：
4 【解析】延长AC,BE交于点F,如图.
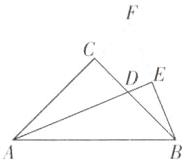
∵AE平分∠CAB,
∴∠EAB=∠EAF.
∵BE⊥AE,
∴∠AEB=∠AEF=90°.在△ABE与△AFE中,∠EAB=∠EAF,AE=AE,∠AEB=∠AEF,
∴△ABE≌△AFE(ASA),
∴BE=FE,
∴BF=2BE=4.
∵∠ACB=∠AEB=90°,∠ADC=∠EDB,
∴∠CAD=∠CBF.在△ACD与△BCF中,∠CAD=∠CBF,AC=BC,∠ACD=∠BCF=90°,
∴△ACD≌△BCF(ASA),
∴AD=BF=4,
∴△ABD的面积为$\frac{1}{2}$·AD·BE=$\frac{1}{2}$×4×2=4. 故答案为4.

4 [2025 江苏连云港期末,中]如图,AE 与 BD 相交于点 C,AC= EC,BC= DC,AB= 4cm,点 P 从点 A 出发,沿 A→B→A 方向以 3cm/s 的速度运动,点 Q 从点 D 出发,沿 D→E 方向以 1cm/s 的速度运动,P,Q 两点同时出发,当点 P 返回到点 A 时,P,Q 两点同时停止运动. 设点 P 的运动时间为 t s. 连接 PQ,当线段 PQ 经过点 C 时,求 t 的值.

答案： 【解】如图,在△ABC和△EDC中,AC=EC,∠ACB=∠ECD,BC=DC,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,ED=AB=4cm. 在△ACP和△ECQ中,∠A=∠E,AC=CE,∠ACP=∠ECQ,
∴△ACP≌△ECQ(ASA),
∴AP=EQ.当0≤t≤$\frac{4}{3}$时,3t=4 - t,解得t=1;当$\frac{4}{3}$＜t≤$\frac{8}{3}$时,8 - 3t=4 - t,解得t=2. 综上所述,当线段PQ经过点C时,t的值为1或2.

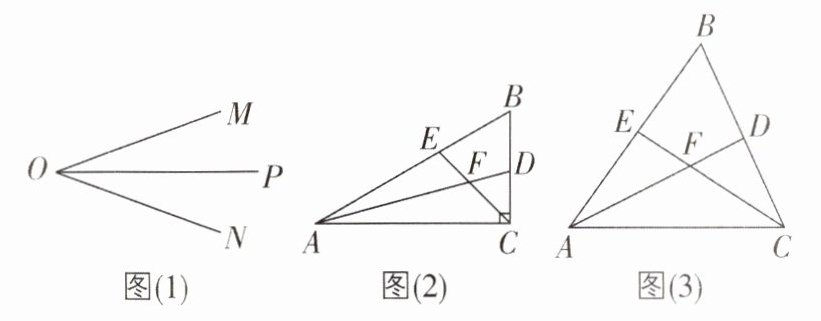
5 核心素养 模型观念 [较难]如图(1),OP 是∠MON 的平分线,请你利用该图形画一对以 OP 所在直线为对称轴的全等三角形,并写出添加的全等条件.
请你参考这个作全等三角形的方法,解答下列问题：
(1)如图(2),在△ABC 中,∠ACB 是直角,∠B= 60°,AD,CE 分别是∠BAC 和∠BCA 的平分线,AD,CE 相交于点 F,求∠EFA 的度数.
(2)在(1)的条件下,请判断 FE 与 FD 之间的数量关系,并说明理由.
(3)如图(3),在△ABC 中,如果∠ACB 不是直角,而(1)中的其他条件不变,试问(2)中所得结论是否仍然成立？若成立,请证明；若不成立,请说明理由.

答案：
【解】如图,添加的全等条件为OB=OC,则连接FG,证明△BOD≌△COD(SAS).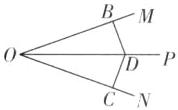
(1)
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°.
∵AD,CE分别是∠BAC和∠BCA的平分线,
∴∠DAC=$\frac{1}{2}$∠BAC=15°,∠ECA=$\frac{1}{2}$∠ACB=45°,
∴∠EFA=∠DAC+∠ECA=15°+45°=60°.
(2)FE=FD. 理由如下:在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF.在△EAF和△GAF中,AE=AG,∠EAF=∠FAG,AF=AF,
∴△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA=60°,
∴∠GFC=180° - 60° - 60°=60°.又
∵∠DFC=∠EFA=60°,
∴∠DFC=∠GFC.在△FDC和△FGC中,∠DFC=∠GFC,FC=FC,∠FCD=∠FCG,
∴△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
(3)
(2)中的结论FE=FD仍然成立. 证明:在AC上截取AH=AE,连接FH. 同
(2)可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA.又由
(1)知∠FAC=$\frac{1}{2}$∠BAC,∠FCA=$\frac{1}{2}$∠ACB,
∴∠FAC+∠FCA=$\frac{1}{2}$(∠BAC+∠ACB)=$\frac{1}{2}$(180° - ∠B)=60°,
∴∠AFC=180° - (∠FAC+∠FCA)=120°,
∴∠EFA=∠HFA=180° - 120°=60°,
∴∠HFC=60°=∠DFC. 同
(2)可得△FDC≌△FHC,
∴FD=FH,
∴FE=FD.