第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1已知点$P(x,|x|)$,则点P一定(
A.在第一象限
B.在第一或第四象限
C.在x轴上方
D.不在x轴下方
D
)A.在第一象限
B.在第一或第四象限
C.在x轴上方
D.不在x轴下方
答案:
1.D [解析]已知点P(x,|x|),其中|x|≥0.当|x|>0时,点P在x轴的上方;当|x|=0时,点P在x轴上,只有D选项符合.故选D.
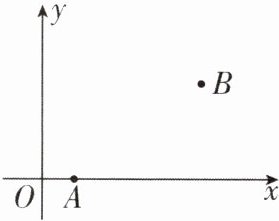
2[2025贵州贵阳期中]如图,已知在平面直角坐标系内有两点$A(1,0),B(5,3)$,在x轴上有一点C,使得三角形ABC为等腰三角形,则满足条件的点C的个数为( )
A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
2.D [解析]连接AB,作BE⊥x轴于点E,如图所示.
∵A(1,0),B(5,3),
∴AB=5.以A为圆心,AB长为半径作弧,交x轴于C₁和C₂,则AC₁=AC₂=5,
∴OC₁=4,OC₂=6,
∴C₁(−4,0),C₂(6,0);以B为圆心,AB长为半径作弧,交x轴于C₃(除点A),则易知AE=EC₃=4,
∴OC₃=9,
∴C₃(9,0).作AB的垂直平分线,交x轴于C₄,交AB于D,连接BC₄,则BD=2.5.设C₄(x,0),则BC₄=AC₄=x - 1,EC₄=5 - x.在Rt△BC₄E中,由勾股定理得(x - 1)²=3²+(5 - x)²,解得x=$\frac{33}{8}$,
∴C₄($\frac{33}{8}$,0).综上所述,满足条件的点C有4个.故选D.

2.D [解析]连接AB,作BE⊥x轴于点E,如图所示.
∵A(1,0),B(5,3),
∴AB=5.以A为圆心,AB长为半径作弧,交x轴于C₁和C₂,则AC₁=AC₂=5,
∴OC₁=4,OC₂=6,
∴C₁(−4,0),C₂(6,0);以B为圆心,AB长为半径作弧,交x轴于C₃(除点A),则易知AE=EC₃=4,
∴OC₃=9,
∴C₃(9,0).作AB的垂直平分线,交x轴于C₄,交AB于D,连接BC₄,则BD=2.5.设C₄(x,0),则BC₄=AC₄=x - 1,EC₄=5 - x.在Rt△BC₄E中,由勾股定理得(x - 1)²=3²+(5 - x)²,解得x=$\frac{33}{8}$,
∴C₄($\frac{33}{8}$,0).综上所述,满足条件的点C有4个.故选D.

3[2025江苏泰州期中]平面直角坐标系中,已知点$A(3,2)$,直线$AB// y$轴,且$AB= 4$,则点B坐标为____.
答案:
3.(3,6)或(3,−2) [解析]设点B的坐标为(x,y).
∵AB//y轴,A(3,2),
∴x=3.
∵AB=4,
∴|y - 2|=4,
∴y - 2=±4,
∴y=6或 - 2,
∴点B的坐标为(3,6)或(3,−2),故答案为(3,6)或(3,−2)
∵AB//y轴,A(3,2),
∴x=3.
∵AB=4,
∴|y - 2|=4,
∴y - 2=±4,
∴y=6或 - 2,
∴点B的坐标为(3,6)或(3,−2),故答案为(3,6)或(3,−2)
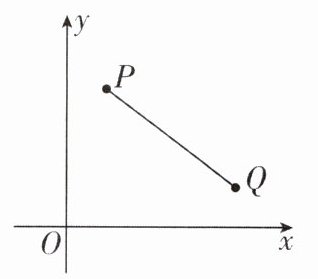
4[2024江苏扬州邗江区调研]如图,在第一象限内有$P(m-4,n),Q(m,n-3)$两点,将线段PQ平移,使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是____.

答案:
4.(0,3)或(−4,0) [解析]设平移后点P,Q的对应点分别是P',Q'.分两种情况:①若P'在y轴上,Q'在x轴上,则P'横坐标为0,Q'纵坐标为0.
∵0 - (n - 3)= - n + 3,
∴n - n + 3=3,
∴点P平移后的对应点的坐标是(0,3).②若P'在x轴上,Q'在y轴上,则P'纵坐标为0,Q'横坐标为0.
∵0 - m= - m,
∴m - 4 - m= - 4,
∴点P平移后的对应点的坐标是(−4,0).综上可知,点P平移后的对应点的坐标是(0,3)或(−4,0).故答案为(0,3)或(−4,0).
∵0 - (n - 3)= - n + 3,
∴n - n + 3=3,
∴点P平移后的对应点的坐标是(0,3).②若P'在x轴上,Q'在y轴上,则P'纵坐标为0,Q'横坐标为0.
∵0 - m= - m,
∴m - 4 - m= - 4,
∴点P平移后的对应点的坐标是(−4,0).综上可知,点P平移后的对应点的坐标是(0,3)或(−4,0).故答案为(0,3)或(−4,0).
5如图,一个粒子在第一象限内及x轴、y轴上运动,第1次,它从原点运动到点$(1,0)$;第2次,它从点$(1,0)运动到点(1,1)$,而后它接着按图中箭头所示在与x轴、y轴平行的方向上来回运动,且每次运动1个单位长度,那么第2023次,这个粒子所在位置的坐标是______
(44,1)
.
答案:
(44,1) [解析]由题意知(0,0)表示粒子运动了0次,(1,1)表示粒子运动了1×2=2(次),粒子将向左运动,(2,2)表示粒子运动了2×3=6(次),粒子将向下运动,(3,3)表示粒子运动了3×4=12(次),粒子将向左运动,…,
∴(44,44)表示粒子运动了44×45=1980(次),此时粒子将向下运动,
∴到第2023次,粒子又向下运动了2023 - 1980=43(个)单位长度.
∵44 - 43=1,
∴粒子所在位置的坐标是(44,1),故答案为(44,1).
∴(44,44)表示粒子运动了44×45=1980(次),此时粒子将向下运动,
∴到第2023次,粒子又向下运动了2023 - 1980=43(个)单位长度.
∵44 - 43=1,
∴粒子所在位置的坐标是(44,1),故答案为(44,1).
6[2025江苏南京期中]$△ABC$在如图所示的正方形网格中,已知点A的坐标为$(0,-3)$,点B的坐标为$(3,-1)$.
(1)在网格中画出平面直角坐标系,并写出点C的坐标为____;
(2)作$△ABC$关于y轴对称的$△A'B'C'$;
(3)若P为x轴上一点,且$△PAB$的面积为4,求点P的坐标.

答案:
(1)(3,3) [解析]画出的平面直角坐标系如图
(1)所示,点C的坐标为(3,3).故答案为(3,3).
(2)如图
(2)所示,△A'B'C'即为所求.
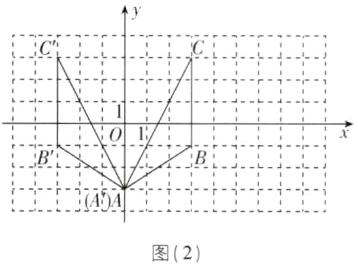
(3)如图
(3),延长AB交x轴于Q,设BC交x轴于M,则MB⊥x轴.设点Q的坐标为(a,0),则MQ=a - 3,OQ=a.
∵$S_{梯形ABMO}=S_{△AOQ} - S_{△BMQ}$,即$\frac{1}{2}$×(1+3)×3=$\frac{1}{2}$×3a - $\frac{1}{2}$×1×(a - 3),解得a=$\frac{9}{2}$.设点P的坐标为(t,0).
∵$S_{△PAB}=S_{△APQ} - S_{△BPQ}$=4,即$\frac{1}{2}$PQ·|yA| - $\frac{1}{2}$PQ·|yB|=4,则PQ=$|\frac{9}{2}-t|$=4,
∴t=$\frac{1}{2}$或t=$\frac{17}{2}$.综上可知,点P的坐标为($\frac{1}{2}$,0)或($\frac{17}{2}$,0).

(1)(3,3) [解析]画出的平面直角坐标系如图
(1)所示,点C的坐标为(3,3).故答案为(3,3).
(2)如图
(2)所示,△A'B'C'即为所求.

(3)如图
(3),延长AB交x轴于Q,设BC交x轴于M,则MB⊥x轴.设点Q的坐标为(a,0),则MQ=a - 3,OQ=a.
∵$S_{梯形ABMO}=S_{△AOQ} - S_{△BMQ}$,即$\frac{1}{2}$×(1+3)×3=$\frac{1}{2}$×3a - $\frac{1}{2}$×1×(a - 3),解得a=$\frac{9}{2}$.设点P的坐标为(t,0).
∵$S_{△PAB}=S_{△APQ} - S_{△BPQ}$=4,即$\frac{1}{2}$PQ·|yA| - $\frac{1}{2}$PQ·|yB|=4,则PQ=$|\frac{9}{2}-t|$=4,
∴t=$\frac{1}{2}$或t=$\frac{17}{2}$.综上可知,点P的坐标为($\frac{1}{2}$,0)或($\frac{17}{2}$,0).

(1)$(\sqrt {2},\sqrt {2})$
(2)当$(a,b)$在坐标轴上时,若$(a,b)$为“n倍理想坐标”,求a,b的值,并指出$(a,b)$在平面直角坐标系中的哪个位置.
(3)若$(a,b)$是象限角平分线上的点(原点除外),求$(a,b)$是几倍理想坐标.
是
“2倍理想坐标”(填“是”或“不是”);$(2,3)$是$\frac{13}{6}$
倍理想坐标.(2)当$(a,b)$在坐标轴上时,若$(a,b)$为“n倍理想坐标”,求a,b的值,并指出$(a,b)$在平面直角坐标系中的哪个位置.
当(a,b)在坐标轴上时,a=0或b=0,∴ab=0.∵(a,b)为“n倍理想坐标”,∴a²+b²=nab=0,∴a=0且b=0,∴(a,b)是平面直角坐标系中的原点.
(3)若$(a,b)$是象限角平分线上的点(原点除外),求$(a,b)$是几倍理想坐标.
若(a,b)是象限角平分线上的点(原点除外),则a=±b≠0.分两种情况:①当(a,b)是第一、三象限角平分线上的点(原点除外)时,a=b.∵a²+b²=2a²=2a·a=2ab,∴(a,b)是“2倍理想坐标”.②当(a,b)是第二、四象限角平分线上的点(原点除外)时,a= - b.∵a²+b²=2a²=2a·( - b)= - 2ab,∴(a,b)是“ - 2倍理想坐标”.综上所述,(a,b)是“2倍理想坐标”或“ - 2倍理想坐标”.
答案:
(1)是,$\frac{13}{6}$ [解析]
∵($\sqrt{2}$)²+($\sqrt{2}$)²=2×$\sqrt{2}$×$\sqrt{2}$,
∴($\sqrt{2}$,$\sqrt{2}$)是“2倍理想坐标”;
∵2²+3²=$\frac{13}{6}$×2×3,
∴(2,3)是“$\frac{13}{6}$倍理想坐标”.故答案为是,$\frac{13}{6}$.
(2)当(a,b)在坐标轴上时,a=0或b=0,
∴ab=0.
∵(a,b)为“n倍理想坐标”,
∴a²+b²=nab=0,
∴a=0且b=0,
∴(a,b)是平面直角坐标系中的原点.
(3)若(a,b)是象限角平分线上的点(原点除外),则a=±b≠0.分两种情况:①当(a,b)是第一、三象限角平分线上的点(原点除外)时,a=b.
∵a²+b²=2a²=2a·a=2ab,
∴(a,b)是“2倍理想坐标”.②当(a,b)是第二、四象限角平分线上的点(原点除外)时,a= - b.
∵a²+b²=2a²=2a·( - b)= - 2ab,
∴(a,b)是“ - 2倍理想坐标”.综上所述,(a,b)是“2倍理想坐标”或“ - 2倍理想坐标”.
(1)是,$\frac{13}{6}$ [解析]
∵($\sqrt{2}$)²+($\sqrt{2}$)²=2×$\sqrt{2}$×$\sqrt{2}$,
∴($\sqrt{2}$,$\sqrt{2}$)是“2倍理想坐标”;
∵2²+3²=$\frac{13}{6}$×2×3,
∴(2,3)是“$\frac{13}{6}$倍理想坐标”.故答案为是,$\frac{13}{6}$.
(2)当(a,b)在坐标轴上时,a=0或b=0,
∴ab=0.
∵(a,b)为“n倍理想坐标”,
∴a²+b²=nab=0,
∴a=0且b=0,
∴(a,b)是平面直角坐标系中的原点.
(3)若(a,b)是象限角平分线上的点(原点除外),则a=±b≠0.分两种情况:①当(a,b)是第一、三象限角平分线上的点(原点除外)时,a=b.
∵a²+b²=2a²=2a·a=2ab,
∴(a,b)是“2倍理想坐标”.②当(a,b)是第二、四象限角平分线上的点(原点除外)时,a= - b.
∵a²+b²=2a²=2a·( - b)= - 2ab,
∴(a,b)是“ - 2倍理想坐标”.综上所述,(a,b)是“2倍理想坐标”或“ - 2倍理想坐标”.
查看更多完整答案,请扫码查看


