第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
如图,在△ABC中,∠C= 90°,AC= 12,BC= 6,P,Q两点分别在AC和过点A且垂直于AC的射线AX上运动,PQ= AB,当△PAQ与△ABC全等时,AP的长度为 (
A.6
B.6或12
C.8
D.8或12
B
)A.6
B.6或12
C.8
D.8或12
答案:
B [解析]
∵∠C = 90°,AX⊥AC,
∴∠C = ∠QAP = 90°。①当AP = BC = 6时,在Rt△ACB和Rt△QAP中,{AB = QP,BC = AP},
∴Rt△ACB≌Rt△QAP(HL)。②当AP = AC = 12时,在Rt△ACB和Rt△PAQ中,{AB = QP,AC = AP},
∴Rt△ACB≌Rt△PAQ(HL)。综上所述,当△PAQ与△ABC全等时,AP的长度为6或12。故选B。
∵∠C = 90°,AX⊥AC,
∴∠C = ∠QAP = 90°。①当AP = BC = 6时,在Rt△ACB和Rt△QAP中,{AB = QP,BC = AP},
∴Rt△ACB≌Rt△QAP(HL)。②当AP = AC = 12时,在Rt△ACB和Rt△PAQ中,{AB = QP,AC = AP},
∴Rt△ACB≌Rt△PAQ(HL)。综上所述,当△PAQ与△ABC全等时,AP的长度为6或12。故选B。
如图所示,在△ABC中,∠ABC= 90°,延长AB至点E,使AE= AC,过E作EF⊥AC于点F,EF交BC于点G,连接AG,若∠C= 40°,则∠EAG的度数是 (
A.25°
B.20°
C.30°
D.35°
A
)A.25°
B.20°
C.30°
D.35°
答案:
A [解析]
∵∠ABC = 90°,EF⊥AC,
∴∠ABC = ∠AFE = 90°。在△AEF与△ACB中,{∠EAF = ∠CAB,∠AFE = ∠ABC,AE = AC},
∴△AEF≌△ACB(AAS),
∴AF = AB。
∵∠ABC = 90°,∠C = 40°,
∴∠BAC = 50°。在Rt△ABG和Rt△AFG中,{AG = AG,AB = AF},
∴Rt△ABG≌Rt△AFG(HL),
∴∠EAG = ∠FAG = $\frac{1}{2}$×50° = 25°。故选A。
∵∠ABC = 90°,EF⊥AC,
∴∠ABC = ∠AFE = 90°。在△AEF与△ACB中,{∠EAF = ∠CAB,∠AFE = ∠ABC,AE = AC},
∴△AEF≌△ACB(AAS),
∴AF = AB。
∵∠ABC = 90°,∠C = 40°,
∴∠BAC = 50°。在Rt△ABG和Rt△AFG中,{AG = AG,AB = AF},
∴Rt△ABG≌Rt△AFG(HL),
∴∠EAG = ∠FAG = $\frac{1}{2}$×50° = 25°。故选A。
3[2024江苏无锡梁溪区质检,较难]如图,在△ABC中,∠APE= 160°,AP= PE,BP平分∠ABC,则∠ABP= ______°.
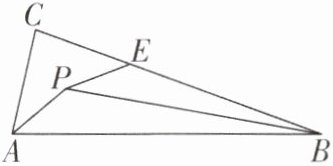

答案:
10 [解析]如图,过P作PM⊥BC于M,PN⊥AB于N,
∴∠PME = ∠PNA = ∠PNB = 90°。
∵BP平分∠ABC,
∴∠PBN = ∠PBM。在△PNB与△PMB中,{∠PNB = ∠PMB,∠PBN = ∠PBM,PB = PB},
∴△PNB≌△PMB(AAS),
∴PN = PM。在Rt△APN与Rt△EPM中,{PA = PE,PN = PM},
∴Rt△APN≌Rt△EPM(HL),
∴∠APN = ∠EPM,
∴∠NPM = ∠APE = 160°,
∴∠ABC = 360° - ∠NPM - ∠PNB - ∠PMB = 20°,
∴∠ABP = $\frac{1}{2}$∠ABC = 10°。故答案为10。

10 [解析]如图,过P作PM⊥BC于M,PN⊥AB于N,
∴∠PME = ∠PNA = ∠PNB = 90°。
∵BP平分∠ABC,
∴∠PBN = ∠PBM。在△PNB与△PMB中,{∠PNB = ∠PMB,∠PBN = ∠PBM,PB = PB},
∴△PNB≌△PMB(AAS),
∴PN = PM。在Rt△APN与Rt△EPM中,{PA = PE,PN = PM},
∴Rt△APN≌Rt△EPM(HL),
∴∠APN = ∠EPM,
∴∠NPM = ∠APE = 160°,
∴∠ABC = 360° - ∠NPM - ∠PNB - ∠PMB = 20°,
∴∠ABP = $\frac{1}{2}$∠ABC = 10°。故答案为10。

4[中]如图,四边形ABCD中,AC为∠BAD的平分线,过点C作CF⊥AD,已知CB= CD.
(1)判断∠ABC与∠ADC之间的数量关系.
(2)若CF= 6,AB= 4,S△ACD= 21,求DF的长.

(1)判断∠ABC与∠ADC之间的数量关系.
(2)若CF= 6,AB= 4,S△ACD= 21,求DF的长.

答案:
(1)[解]如图,过点C作CH⊥AB,交AB的延长线于H。
∵AC平分∠BAD,
∴∠BAC = ∠CAD。在△ACH和△ACF中,{∠BAC = ∠CAD,∠H = ∠AFC = 90°,AC = AC},
∴△ACH≌△ACF(AAS),
∴CH = CF,AH = AF。在Rt△BCH和Rt△DCF中,{CB = CD,CH = CF},
∴Rt△BCH≌Rt△DCF(HL),
∴∠ADC = ∠CBH。
∵∠CBH + ∠ABC = 180°,
∴∠ADC + ∠ABC = 180°。
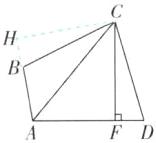
(2)
∵Rt△BCH≌Rt△DCF,
∴BH = DF。
∵S△ACD = 21 = $\frac{1}{2}$×AD×CF,CF = 6,
∴42 = 6AD,
∴AD = 7。
∵AD + AB = AF + FD + AH - BH = 2AF = 7 + 4 = 11,
∴AF = 5.5,
∴DF = AD - AF = 1.5。
(1)[解]如图,过点C作CH⊥AB,交AB的延长线于H。
∵AC平分∠BAD,
∴∠BAC = ∠CAD。在△ACH和△ACF中,{∠BAC = ∠CAD,∠H = ∠AFC = 90°,AC = AC},
∴△ACH≌△ACF(AAS),
∴CH = CF,AH = AF。在Rt△BCH和Rt△DCF中,{CB = CD,CH = CF},
∴Rt△BCH≌Rt△DCF(HL),
∴∠ADC = ∠CBH。
∵∠CBH + ∠ABC = 180°,
∴∠ADC + ∠ABC = 180°。

(2)
∵Rt△BCH≌Rt△DCF,
∴BH = DF。
∵S△ACD = 21 = $\frac{1}{2}$×AD×CF,CF = 6,
∴42 = 6AD,
∴AD = 7。
∵AD + AB = AF + FD + AH - BH = 2AF = 7 + 4 = 11,
∴AF = 5.5,
∴DF = AD - AF = 1.5。
5思想方法转化思想[2025福建莆田调研,较难]我们学习了三角形全等的判定方法(即“SSS”“SAS”“ASA”和“AAS”)和直角三角形全等的特殊判定方法(即“HL”),事实上,在一定条件下,“SSA”是能够用来论证三角形全等的.下面我们对“两个三角形满足两边和其中一边的对角对应相等”的情形进行探究.
在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,对∠B进行分类,可分为∠B是直角、钝角、锐角三种情况进行探究.
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图(1),根据______,可以得到Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图(2),求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)请在图(3)中作△DEF,使得△ABC和△DEF不全等.(尺规作图,不写作法,保留作图痕迹)
(4)当∠B为______时,△ABC≌△DEF.
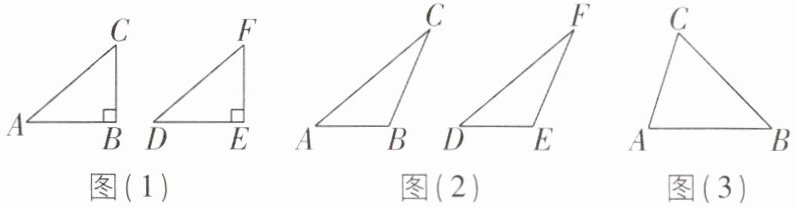
在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,对∠B进行分类,可分为∠B是直角、钝角、锐角三种情况进行探究.
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图(1),根据______,可以得到Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图(2),求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)请在图(3)中作△DEF,使得△ABC和△DEF不全等.(尺规作图,不写作法,保留作图痕迹)
(4)当∠B为______时,△ABC≌△DEF.

答案:
(1)[解]当∠B是直角时,∠B = ∠E = 90°。在Rt△ABC和Rt△DEF中,{AC = DF,BC = EF},
∴Rt△ABC≌Rt△DEF(HL)。故答案为HL。
(2)[证明]过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H,如图
(1),
∴∠G = ∠H = 90°。
∵∠ABC = ∠DEF,且∠ABC,∠DEF都是钝角,
∴∠CBG = 180° - ∠ABC,∠FEH = 180° - ∠DEF,
∴∠CBG = ∠FEH。在△CBG和△FEH中,{∠G = ∠H,∠CBG = ∠FEH,BC = EF},
∴△CBG≌△FEH(AAS),
∴CG = FH。在Rt△ACG和Rt△DFH中,{AC = DF,CG = FH},
∴Rt△ACG≌Rt△DFH(HL),
∴∠A = ∠D。在△ABC和△DEF中,{∠A = ∠D,∠ABC = ∠DEF,AC = DF},
∴△ABC≌△DEF(AAS)。


(3)如图
(2)。
(4)由上可知,当∠B为钝角或直角时,△ABC≌△DEF。故答案为钝角或直角。
(1)[解]当∠B是直角时,∠B = ∠E = 90°。在Rt△ABC和Rt△DEF中,{AC = DF,BC = EF},
∴Rt△ABC≌Rt△DEF(HL)。故答案为HL。
(2)[证明]过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H,如图
(1),
∴∠G = ∠H = 90°。
∵∠ABC = ∠DEF,且∠ABC,∠DEF都是钝角,
∴∠CBG = 180° - ∠ABC,∠FEH = 180° - ∠DEF,
∴∠CBG = ∠FEH。在△CBG和△FEH中,{∠G = ∠H,∠CBG = ∠FEH,BC = EF},
∴△CBG≌△FEH(AAS),
∴CG = FH。在Rt△ACG和Rt△DFH中,{AC = DF,CG = FH},
∴Rt△ACG≌Rt△DFH(HL),
∴∠A = ∠D。在△ABC和△DEF中,{∠A = ∠D,∠ABC = ∠DEF,AC = DF},
∴△ABC≌△DEF(AAS)。


(3)如图
(2)。
(4)由上可知,当∠B为钝角或直角时,△ABC≌△DEF。故答案为钝角或直角。
查看更多完整答案,请扫码查看


