《2025年初中必刷题八年级数学上册苏科版》

如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知$S_{1}+S_{2}= 9$,且$AC+BC= 10$,则AB的长为(D)
A.4
B.6
C.7
D.8

答案： D　[解析]由勾股定理得,AC²+BC²=AB².
∵S₁+S₂=9,
∴$\frac{1}{2}$×π×($\frac{AC}{2}$)²+$\frac{1}{2}$π×($\frac{BC}{2}$)²+$\frac{1}{2}$AC×BC−$\frac{1}{2}$π×($\frac{AB}{2}$)²=9,
∴$\frac{1}{2}$AC×BC=9,
∴AC×BC=18.
∵AC+BC=10,
∴AB²=AC²+BC²=(AC+BC)²−2AC×BC=100−36=8²,
∴AB=8.故选D.

如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },AC= 3,BC= 4,BE平分∠ABC,CD⊥AB$于D,BE与CD相交于F,则CF的长是(B)
A.1
B.$\frac {4}{3}$
C.$\frac {5}{3}$
D.2

答案： B　[解析]过点E作EG⊥AB于点G.
∵CD⊥AB于D,
∴EG//CD,
∴∠GEB=∠EFC.
∵在Rt△ABC中，∠ACB=90°,
∴EC⊥CB.又
∵BE平分∠ABC,EG⊥AB,
∴EG=EC.在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5.在Rt△EBC和Rt△EBG中,{EB=EB,EC=EG},
∴Rt△EBC≌Rt△EBG(HL),
∴∠CEB=∠GEB,BG=BC=4,
∴∠CEB=∠EFC,AG=AB−BG=5−4=1,
∴CF=CE.设CF=EG=EC=x,则AE=3−x.在Rt△AEG中,由勾股定理得(3−x)²=x²+1²,解得x=$\frac{4}{3}$,即CF的长是$\frac{4}{3}$.故选B.

3[2024江苏无锡调研,中]如图所示,折叠长方形的一边AD,使点D落在边BC上的点F处,已知$AB= 8cm,BC= 10cm$,则EC的长为3cm.

答案： 3　[解析]由折叠的性质得△AED≌△AEF,
∴AF=AD=BC=10,DE=EF.设EC=x,则DE=8−x,
∴EF=8−x.在Rt△ABF中，BF²=AF²−AB²=36,
∴BF=6,
∴FC=BC−BF=4.在Rt△CEF中,由勾股定理得CE²+FC²=EF²,即x²+4²=(8−x)²,解得x=3,
∴EC的长为3cm.故答案为3.

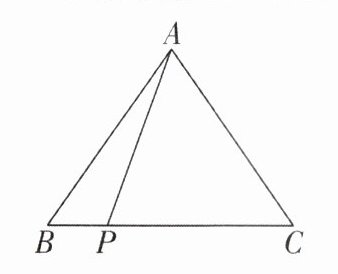
4[2025江苏常州质检]如图,在$△ABC$中,$AB= AC= 4$,P是BC上异于B,C的一点,则$AP^{2}+BP\cdot PC$的值是____.

答案：
16　[解析]如图,过点A作AD⊥BC于点D.
∵AD⊥BC,
∴△ADP与△ABD都为直角三角形,
∴AP²=AD²+DP²,AB²=AD²+BD².
∵AB=AC,AD⊥BC,
∴BD=CD.
∵PC=CD+DP,BD=CD,
∴PC=BD+DP.
∵BP=BD−DP,
∴BP·PC=BD²−DP².
∵AP²=AD²+DP²,
∴AP²+BP·PC=AD²+BD².
∵AB²=AD²+BD²,
∴AP²+BP·PC=16.故答案为16.

5[2024江苏镇江期中,较难]如图,在$△ABC$中,$∠ACB= 90^{\circ },AC= 6,AB= 10$,点O是AB边的中点,点P是射线AC上的一个动点,$BQ// CA$交PO的延长线于点Q,$OM⊥PQ$交BC于点M.当$CP= 1$时,BM的长为____2.5或1.

答案： 2.5或1　[解析]连接PM,QM,设BM=x.当点P在AC上时,
∵在Rt△ABC中,AB=10,AC=6,
∴BC=8,
∴CM=8−x.
∵QB//AP,
∴∠A=∠OBQ.
∵O是AB的中点,
∴OA=OB.在△OAP和△OBQ中，{∠A=∠OBQ,OA=OB,∠AOP=∠BOQ},
∴△OAP≌△OBQ(ASA),
∴PA=BQ=6−1=5,OQ=OP.
∵OM⊥PQ,
∴MQ=MP,
∴BQ²+BM²=CP²+CM²,即5²+x²=1²+(8−x)²,解得x=2.5.当点P在AC的延长线上时,同法可得7²+x²=1²+(8−x)²,解得x=1.综上所述,满足条件的BM的长为2.5或1.故答案为2.5或1.

6[较难]一辆装满货物的卡车,高2.5m,宽1.6m,要开进上边是半圆,下边是长方形的隧道,如图所示,已知半圆的直径为2m,长方形的另一条边长是2.3m.
(1)此卡车是否能通过隧道?试说明你的理由.
(2)为了适应车流量的增加,把隧道改为双行道,要使宽为1.2m,高为2.8m的卡车能安全通过,那么此隧道的宽至少增加到多少?

答案：
[解]
(1)该卡车能通过隧道.理由如下:如图
(1),O为半圆的圆心,MN为卡车的宽度，分别过M,N作AB的垂线交半圆于C,D,连接CD,过O作OE⊥CD,E为垂足,连接OC,易知CD=MN=1.6m,AB=2m,所以CE=DE=0.8m,OC=OA=1m.在Rt△OCE中,OE²=OC²−CE²=0.36,即OE=0.6m,所以CM=2.3+0.6=2.9(m)＞2.5m,所以这辆卡车能通过隧道.
利用勾股定理和平方差公式推出AP²=AD²+DP²,BP·PC=BD²−DP²是解题的关键.
分两种情况讨论:①当点P在AC上时;②当点P在AC的延长线上时，注意不要漏解.
(2)如图
(2),O为半圆的圆心,PL为卡车的宽度，过P作GH的垂线交半圆于I,垂足为F,连接OI,过I作IK⊥LO,交LO的延长线于K.根据题意可知LK=PI=2.8m,IK=OF=PL=1.2m,PF=GJ=2.3m,IF=2.8−2.3=0.5(m).根据勾股定理得OG²=OI²=IF²+OF²=0.5²+1.2²=1.69,即OG=1.3m,所以隧道的宽至少增加到1.3×2=2.6(m).

7思想方法数形结合[2025江苏无锡期中,较难]定义:在$△ABC$中,若$BC= a,AC= b,AB= c,a,b,c满足ac+a^{2}= b^{2}$,则称这个三角形为类勾股三角形.请根据以上定义解决下列问题:
(1)“直角三角形都是类勾股三角形”是____(填“真”或“假”)命题.
(2)如图(1),若等腰三角形ABC是类勾股三角形,其中$AB= BC,AC＞AB$,请求$∠A$的度数.
(3)如图(2),在$△ABC$中,$∠B= 2∠A$,且$∠C＞∠A$,请证明$△ABC$为类勾股三角形.

答案：

(1)[解]在△ABC中,BC=a,AC=b,AB=c,若△ABC是类勾股三角形,则ac+a²=b²;若△ABC是直角三角形,且∠B=90°,由勾股定理得c²+a²=b²,
∴ac+a²=c²+a²,
∴a=c,
∴当直角三角形是等腰直角三角形时,这个直角三角形是类勾股三角形,
∴“直角三角形都是类勾股三角形”是假命题,故答案为假.
(2)[解]
∵AB=BC,AC＞AB,
∴a=c,b＞c.
∵△ABC是类勾股三角形,
∴ac+a²=b²,
∴c²+a²=b²,
∴△ABC是等腰直角三角形,∠B=90°,
∴∠A=45°.
(3)[证明]设CB=a,AC=b,AB=c,在线段AB上取一点D,使AD=CD,连接CD,过C作CE⊥AB交AB于点E,如图.
∵AD=CD,
∴∠ACD=∠A,
∴∠CDB=∠ACD+∠A=2∠A.
∵∠B=2∠A,
∴∠CDB=∠B,
∴CD=CB=a,
∴AD=CD=a,
∴DB=AB−AD=c−a.
∵CE⊥AB,
∴DE=BE=$\frac{1}{2}$(c−a),
∴AE=AD+DE=a+$\frac{1}{2}$(c−a)=$\frac{1}{2}$(a+c).在Rt△ACE中,CE²=AC²−AE²=b²−[$\frac{1}{2}$(c+a)]²;在Rt△BCE中,CE²=BC²−BE²=a²−[$\frac{1}{2}$(c−a)]²,
∴b²−[$\frac{1}{2}$(c+a)]²=a²−[$\frac{1}{2}$(c−a)]²,整理得b²=ac+a²,
∴△ABC是类勾股三角形.