第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2025江苏南通质检,中]已知等腰三角形一腰上的高线与另一腰的夹角为$60^{\circ }$,那么这个等腰三角形的顶角等于( )
A.$15^{\circ }或75^{\circ }$
B.$30^{\circ }$
C.$150^{\circ }$
D.$150^{\circ }或30^{\circ }$
A.$15^{\circ }或75^{\circ }$
B.$30^{\circ }$
C.$150^{\circ }$
D.$150^{\circ }或30^{\circ }$
答案:
D [解析]如图,AB=AC,BD⊥AC.如图
(1),
∵∠ABD=60°,则∠A=30°;如图
(2),
∵∠ABD=60°,
∴∠BAD=30°,
∴∠BAC=180°−30°=150°.故这个等腰三角形的顶角等于30°或150°.
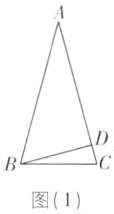

D [解析]如图,AB=AC,BD⊥AC.如图
(1),
∵∠ABD=60°,则∠A=30°;如图
(2),
∵∠ABD=60°,
∴∠BAD=30°,
∴∠BAC=180°−30°=150°.故这个等腰三角形的顶角等于30°或150°.
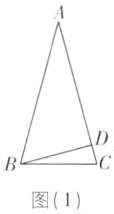

如图,在$△ABC$中,$AB= AC$,E是BC边上一点,将$△ABE$沿AE翻折,使点B落到点D的位置,AD边与BC边交于点F,如果$AE= EF= DF$,那么$∠BAE$的度数为
($\frac{360}{7}$)°
.
答案:
($\frac{360}{7}$)° [解析]
∵AB=AC,
∴∠B=∠C,令∠B=∠C=α,由折叠的性质可得∠D=∠B=α.
∵EF=DF,
∴∠D=∠FED=α,
∴∠AFE=∠D+∠FED=2α.
∵AE=EF,
∴∠EAF=∠AFE=2α.由翻折可知∠BAE=∠EAF=2α,
∴∠AEF=∠B+∠BAE=3α.在△AEF中,∠AFE+∠FEA+∠EAF=180°,即2α+3α+2α=180°,解得α=($\frac{180}{7}$)°,
∴∠BAE=2α=($\frac{360}{7}$)°.故答案为($\frac{360}{7}$)°.
∵AB=AC,
∴∠B=∠C,令∠B=∠C=α,由折叠的性质可得∠D=∠B=α.
∵EF=DF,
∴∠D=∠FED=α,
∴∠AFE=∠D+∠FED=2α.
∵AE=EF,
∴∠EAF=∠AFE=2α.由翻折可知∠BAE=∠EAF=2α,
∴∠AEF=∠B+∠BAE=3α.在△AEF中,∠AFE+∠FEA+∠EAF=180°,即2α+3α+2α=180°,解得α=($\frac{180}{7}$)°,
∴∠BAE=2α=($\frac{360}{7}$)°.故答案为($\frac{360}{7}$)°.
如图,在$△ABC$中,点D为BC边上一点,$BD= BA$.EF垂直平分AC,交AC于点E,交BC于点F,连接AF,AD.当$∠B= 30^{\circ },∠BAF= 90^{\circ }$时,$∠DAC$的度数为
45
$^{\circ }$.
答案:
45 [解析]
∵BA=BD,∠B=30°,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°−∠B)=75°.
∵∠BAF=90°,
∴∠AFB=90°−∠B=60°,
∴∠C+∠CAF=60°.
∵EF垂直平分AC,
∴FA=FC,
∴∠C=∠CAF=30°,
∴∠DAC=∠ADB−∠C=45°.故答案为45.
∵BA=BD,∠B=30°,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°−∠B)=75°.
∵∠BAF=90°,
∴∠AFB=90°−∠B=60°,
∴∠C+∠CAF=60°.
∵EF垂直平分AC,
∴FA=FC,
∴∠C=∠CAF=30°,
∴∠DAC=∠ADB−∠C=45°.故答案为45.
4 [2024陕西西安临潼区期中,中]如图,等腰$△ABC$底边BC的长为6 cm,面积是$18cm^{2}$,腰AB的垂直平分线EF交AC于点F,交AB于点E,若D为BC 边上的中点,M为线段EF上一个动点,则$△BDM$周长的最小值为____
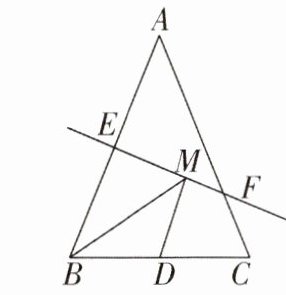
9
cm.
答案:
9 [解析]连接AM,AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴BD=$\frac{1}{2}$BC=3cm,AD⊥BC,S△ABC=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×6×AD=18cm²,
∴AD=6cm.
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴△BDM的周长为BM+MD+BD=AM+DM+3.又
∵AM+DM≥AD,
∴当A,M,D三点共线时,△BDM周长有最小值,为AD+3=6+3=9(cm).故答案为9.
∵△ABC是等腰三角形,点D是BC边的中点,
∴BD=$\frac{1}{2}$BC=3cm,AD⊥BC,S△ABC=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×6×AD=18cm²,
∴AD=6cm.
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴△BDM的周长为BM+MD+BD=AM+DM+3.又
∵AM+DM≥AD,
∴当A,M,D三点共线时,△BDM周长有最小值,为AD+3=6+3=9(cm).故答案为9.
5 [2024江苏无锡质检,较难]在$△ABC$中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G,若$∠EAG= 30^{\circ }$,则$∠BAC= $____.
答案:
75°或105° [解析]当∠BAC为锐角时,如图
(1).设∠BAG=α,∠CAE=β.
∵∠EAG=30°,
∴∠EAB=∠EAG+∠BAG=30°+α,∠CAG=∠CAE+∠EAG=β+30°,∠BAC=α+β+30°.
∵DE,FG分别垂直平分AB,AC,
∴∠B=∠EAB,∠C=∠CAG.
∵∠BAC+∠B+∠C=180°,
∴α+β+30°+30°+α+β+30°=180°,
∴α+β=45°,
∴∠BAC=α+β+30°=45°+30°=75°.
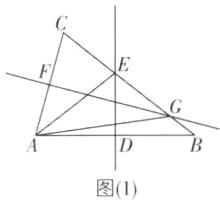
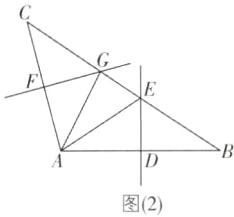
当∠BAC为钝角时,如图
(2).
∵DE,FG分别垂直平分AB,AC,
∴∠B=∠EAB,∠C=∠CAG,
∴∠BAC=∠EAB+∠EAG+∠CAG=∠B+30°+∠C.
∵∠BAC+∠B+∠C=180°,
∴∠B+30°+∠C+∠B+∠C=180°,
∴∠B+∠C=75°,
∴∠BAC=180°−75°=105°.综上所述,∠BAC=75°或105°.故答案为75°或105°.
75°或105° [解析]当∠BAC为锐角时,如图
(1).设∠BAG=α,∠CAE=β.
∵∠EAG=30°,
∴∠EAB=∠EAG+∠BAG=30°+α,∠CAG=∠CAE+∠EAG=β+30°,∠BAC=α+β+30°.
∵DE,FG分别垂直平分AB,AC,
∴∠B=∠EAB,∠C=∠CAG.
∵∠BAC+∠B+∠C=180°,
∴α+β+30°+30°+α+β+30°=180°,
∴α+β=45°,
∴∠BAC=α+β+30°=45°+30°=75°.


当∠BAC为钝角时,如图
(2).
∵DE,FG分别垂直平分AB,AC,
∴∠B=∠EAB,∠C=∠CAG,
∴∠BAC=∠EAB+∠EAG+∠CAG=∠B+30°+∠C.
∵∠BAC+∠B+∠C=180°,
∴∠B+30°+∠C+∠B+∠C=180°,
∴∠B+∠C=75°,
∴∠BAC=180°−75°=105°.综上所述,∠BAC=75°或105°.故答案为75°或105°.
6 [中]如图,在$△ABC$中,$AB= AC$,点O在高AE上,且$OA= OB$,连接BO并延长交AC于点D.
(1)求证:$∠BAC= 2∠ABD$.
(2)若$△BCD$是等腰三角形,求$∠BAC$的度数.
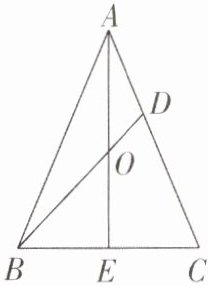
(1)求证:$∠BAC= 2∠ABD$.
(2)若$△BCD$是等腰三角形,求$∠BAC$的度数.

答案:
(1)[证明]
∵AB=AC,AE⊥BC,
∴∠BAC=2∠BAE.
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD.
(2)[解]①当BD=BC时,∠C=∠BDC.
∵∠ABD=∠BAE=∠CAE,
∴∠BDC=∠ABD+∠BAC=3∠ABD.设∠ABD=α,则∠BAC=2α,∠BDC=∠C=∠ABC=3α,
∴2α+3α+3α=180°,
∴α=22.5°,
∴2α=45°,
∴∠BAC=45°.
②当BC=CD时,∠CBD=∠CDB,
∴∠CBD=∠CDB=3∠ABD.设∠ABD=β,则∠BAC=2β,∠CBD=∠CDB=3β,
∴∠ABC=∠C=4β.
∵∠ABC+∠C+∠BAC=180°,
∴4β+4β+2β=180°,
∴β=18°,
∴2β=36°,
∴∠BAC=36°.
综上所述,∠BAC的度数为45°或36°.
(1)[证明]
∵AB=AC,AE⊥BC,
∴∠BAC=2∠BAE.
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD.
(2)[解]①当BD=BC时,∠C=∠BDC.
∵∠ABD=∠BAE=∠CAE,
∴∠BDC=∠ABD+∠BAC=3∠ABD.设∠ABD=α,则∠BAC=2α,∠BDC=∠C=∠ABC=3α,
∴2α+3α+3α=180°,
∴α=22.5°,
∴2α=45°,
∴∠BAC=45°.
②当BC=CD时,∠CBD=∠CDB,
∴∠CBD=∠CDB=3∠ABD.设∠ABD=β,则∠BAC=2β,∠CBD=∠CDB=3β,
∴∠ABC=∠C=4β.
∵∠ABC+∠C+∠BAC=180°,
∴4β+4β+2β=180°,
∴β=18°,
∴2β=36°,
∴∠BAC=36°.
综上所述,∠BAC的度数为45°或36°.
7 [2024湖南娄底期中,中]如图,在等腰$△ABC$中,$AB= AC$,点D在BC上,且$AD= AE$.
(1)若$∠BAC= 90^{\circ },∠BAD= 30^{\circ }$,求$∠EDC$的度数.
(2)若$∠BAC= α(α>30^{\circ }),∠BAD= 30^{\circ }$,求$∠EDC$的度数.
(3)猜想$∠EDC与∠BAD$的数量关系.(不必证明)
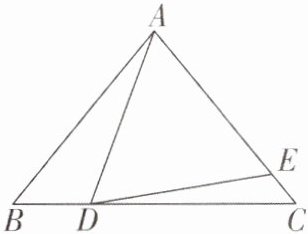
(1)若$∠BAC= 90^{\circ },∠BAD= 30^{\circ }$,求$∠EDC$的度数.
(2)若$∠BAC= α(α>30^{\circ }),∠BAD= 30^{\circ }$,求$∠EDC$的度数.
(3)猜想$∠EDC与∠BAD$的数量关系.(不必证明)

答案:
(1)[解]
∵∠BAC=90°,AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=45°,
∴∠ADC=∠B+∠BAD=45°+30°=75°.
∵∠DAC=∠BAC−∠BAD=90°−30°=60°,AD=AE,
∴∠ADE=∠AED=$\frac{1}{2}$(180°−∠DAC)=60°,
∴∠EDC=∠ADC−∠ADE=75°−60°=15°.
(2)[解]
∵∠BAC=α,AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=90°−$\frac{1}{2}$α,
∴∠ADC=∠B+∠BAD=90°−$\frac{1}{2}$α+30°=120°−$\frac{1}{2}$α.
∵AD=AE,∠DAC=∠BAC−∠BAD=α−30°,
∴∠ADE=∠AED=$\frac{1}{2}$(180°−∠DAC)=105°−$\frac{1}{2}$α,
∴∠EDC=∠ADC−∠ADE=(120°−$\frac{1}{2}$α)−(105°−$\frac{1}{2}$α)=15°,即∠EDC的度数是15°.
(3)∠EDC与∠BAD的数量关系是∠EDC=$\frac{1}{2}$∠BAD.
(1)[解]
∵∠BAC=90°,AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=45°,
∴∠ADC=∠B+∠BAD=45°+30°=75°.
∵∠DAC=∠BAC−∠BAD=90°−30°=60°,AD=AE,
∴∠ADE=∠AED=$\frac{1}{2}$(180°−∠DAC)=60°,
∴∠EDC=∠ADC−∠ADE=75°−60°=15°.
(2)[解]
∵∠BAC=α,AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=90°−$\frac{1}{2}$α,
∴∠ADC=∠B+∠BAD=90°−$\frac{1}{2}$α+30°=120°−$\frac{1}{2}$α.
∵AD=AE,∠DAC=∠BAC−∠BAD=α−30°,
∴∠ADE=∠AED=$\frac{1}{2}$(180°−∠DAC)=105°−$\frac{1}{2}$α,
∴∠EDC=∠ADC−∠ADE=(120°−$\frac{1}{2}$α)−(105°−$\frac{1}{2}$α)=15°,即∠EDC的度数是15°.
(3)∠EDC与∠BAD的数量关系是∠EDC=$\frac{1}{2}$∠BAD.
某数学兴趣小组开展了一次活动,过程如下:如图,已知$∠BAC= θ(0^{\circ }<θ<90^{\circ })$.现把等长的小棒依次摆放在射线AB,AC之间,并使小棒两端分别落在射线AB,AC上.$A_{1}A_{2}$为第一根小棒,且$A_{1}A_{2}= AA_{1}$,若只能摆放4根小棒,则θ的范围为
18°≤θ<22.5°
.
答案:
18°≤θ<22.5° [解析]
∵AA₁=A₁A₂,
∴∠AA₂A₁=∠A,
∴∠A₂A₁A₃=∠AA₂A₁+∠A=2∠BAC=2θ.
∵A₁A₂=A₂A₃,
∴∠A₂A₁A₃=∠A₂A₃A₁=2θ,
∴∠A₃A₂A₄=∠A+∠A₂A₁A₃=θ+2θ=3θ.
∵A₂A₃=A₃A₄,
∴∠A₃A₂A₄=∠A₃A₄A=3θ,
∴∠A₄A₃C=∠A₃A₄A+∠A=4θ.同理,∠A₅A₄B=5θ.
∵只能摆放4根小棒,
∴4θ<90°且5θ≥90°,解得18°≤θ<22.5°,故答案为18°≤θ<22.5°.
∵AA₁=A₁A₂,
∴∠AA₂A₁=∠A,
∴∠A₂A₁A₃=∠AA₂A₁+∠A=2∠BAC=2θ.
∵A₁A₂=A₂A₃,
∴∠A₂A₁A₃=∠A₂A₃A₁=2θ,
∴∠A₃A₂A₄=∠A+∠A₂A₁A₃=θ+2θ=3θ.
∵A₂A₃=A₃A₄,
∴∠A₃A₂A₄=∠A₃A₄A=3θ,
∴∠A₄A₃C=∠A₃A₄A+∠A=4θ.同理,∠A₅A₄B=5θ.
∵只能摆放4根小棒,
∴4θ<90°且5θ≥90°,解得18°≤θ<22.5°,故答案为18°≤θ<22.5°.
查看更多完整答案,请扫码查看


