第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
在$\triangle ABC$中,$AD为BC$边上的中线,若$\triangle ABD与\triangle ADC$的周长差为5,$AC= 8$,则$AB$的长为 (
A.2
B.13
C.3或13
D.2或12
C
)A.2
B.13
C.3或13
D.2或12
答案:
C 【解析】①当△ABD 的周长大于△ADC 的周长时,
∵AD 为 BC 边上的中线,
∴BD=CD,
∴△ABD 与△ADC 的周长差=(AB+AD+BD)-(AC+AD+CD)=AB-AC.
∵△ABD 与△ADC 的周长差为 5,AC=8,
∴AB-8=5,解得 AB=13.②当△ADC 的周长大于△ABD 的周长时,
∵AD 为 BC 边上的中线,
∴BD=CD,
∴△ADC 与△ABD 的周长差=(AC+AD+CD)-(AB+AD+BD)=AC-AB.
∵△ABD 与△ADC 的周长差为 5,AC=8,
∴8-AB=5,解得 AB=3.综上,AB=3 或 13,故选 C.
∵AD 为 BC 边上的中线,
∴BD=CD,
∴△ABD 与△ADC 的周长差=(AB+AD+BD)-(AC+AD+CD)=AB-AC.
∵△ABD 与△ADC 的周长差为 5,AC=8,
∴AB-8=5,解得 AB=13.②当△ADC 的周长大于△ABD 的周长时,
∵AD 为 BC 边上的中线,
∴BD=CD,
∴△ADC 与△ABD 的周长差=(AC+AD+CD)-(AB+AD+BD)=AC-AB.
∵△ABD 与△ADC 的周长差为 5,AC=8,
∴8-AB=5,解得 AB=3.综上,AB=3 或 13,故选 C.
在等腰三角形$ABC$中,$AB= AC$,若中线$BD$将该三角形的周长分为5和3两个部分,则该等腰三角形的底边长为 (
A.$\frac{4}{3}$
B.4
C.$\frac{4}{3}$或4
D.$\frac{5}{3}$或4
A
)A.$\frac{4}{3}$
B.4
C.$\frac{4}{3}$或4
D.$\frac{5}{3}$或4
答案:
A 【解析】设腰长 AB=AC=x,底边长 BC=y.
∵BD 是中线,
∴AD=CD=$\frac{1}{2}$AC=$\frac{1}{2}$x.
∵中线 BD 将该三角形的周长分为 5 和 3 两个部分,
∴$\begin{cases} AB+AD=5, \\ BC+CD=3 \end{cases}$或$\begin{cases} AB+AD=3, \\ BC+CD=5, \end{cases}$
∴$\begin{cases} x+\frac{1}{2}x=5, \\ y+\frac{1}{2}x=3 \end{cases}$或$\begin{cases} x+\frac{1}{2}x=3, \\ y+\frac{1}{2}x=5 \end{cases}$解得$\begin{cases} x=\frac{10}{3}, \\ y=\frac{4}{3} \end{cases}$或$\begin{cases} x=2, \\ y=4. \end{cases}$当等腰三角形 ABC 腰长为$\frac{10}{3}$,底边长为$\frac{4}{3}$时,$\frac{10}{3}+\frac{4}{3}>\frac{10}{3}$,可以组成三角形;当等腰三角形 ABC 腰长为 2,底边长为 4 时,2+2=4,不可以组成三角形,
∴该等腰三角形的底边长为$\frac{4}{3}$,故选 A.
∵BD 是中线,
∴AD=CD=$\frac{1}{2}$AC=$\frac{1}{2}$x.
∵中线 BD 将该三角形的周长分为 5 和 3 两个部分,
∴$\begin{cases} AB+AD=5, \\ BC+CD=3 \end{cases}$或$\begin{cases} AB+AD=3, \\ BC+CD=5, \end{cases}$
∴$\begin{cases} x+\frac{1}{2}x=5, \\ y+\frac{1}{2}x=3 \end{cases}$或$\begin{cases} x+\frac{1}{2}x=3, \\ y+\frac{1}{2}x=5 \end{cases}$解得$\begin{cases} x=\frac{10}{3}, \\ y=\frac{4}{3} \end{cases}$或$\begin{cases} x=2, \\ y=4. \end{cases}$当等腰三角形 ABC 腰长为$\frac{10}{3}$,底边长为$\frac{4}{3}$时,$\frac{10}{3}+\frac{4}{3}>\frac{10}{3}$,可以组成三角形;当等腰三角形 ABC 腰长为 2,底边长为 4 时,2+2=4,不可以组成三角形,
∴该等腰三角形的底边长为$\frac{4}{3}$,故选 A.
如图,$D,E,F分别是边BC$,$AD$,$AC$上的中点,若阴影部分的面积为6,则$\triangle ABC$的面积是 (
A.12
B.14
C.15
D.16
D
)A.12
B.14
C.15
D.16
答案:
D 【解析】
∵D,E,F 分别是边 BC,AD,AC 上的中点,
∴$S_{\triangle ABD}=S_{\triangle ADC}=\frac{1}{2}S_{\triangle ABC}$,$S_{\triangle BDE}=\frac{1}{2}S_{\triangle ABD}$,$S_{\triangle ADF}=\frac{1}{2}S_{\triangle ADC}$,$S_{\triangle DEF}=\frac{1}{2}S_{\triangle ADF}$,
∴$S_{\triangle BDE}=\frac{1}{4}S_{\triangle ABC}$,$S_{\triangle DEF}=\frac{1}{8}S_{\triangle ABC}$,
∴$S_{阴影部分}=S_{\triangle BDE}+S_{\triangle DEF}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{8}S_{\triangle ABC}=\frac{3}{8}S_{\triangle ABC}$,
∴$S_{\triangle ABC}=\frac{8}{3}S_{阴影部分}=\frac{8}{3}×6=16$,故选 D.
∵D,E,F 分别是边 BC,AD,AC 上的中点,
∴$S_{\triangle ABD}=S_{\triangle ADC}=\frac{1}{2}S_{\triangle ABC}$,$S_{\triangle BDE}=\frac{1}{2}S_{\triangle ABD}$,$S_{\triangle ADF}=\frac{1}{2}S_{\triangle ADC}$,$S_{\triangle DEF}=\frac{1}{2}S_{\triangle ADF}$,
∴$S_{\triangle BDE}=\frac{1}{4}S_{\triangle ABC}$,$S_{\triangle DEF}=\frac{1}{8}S_{\triangle ABC}$,
∴$S_{阴影部分}=S_{\triangle BDE}+S_{\triangle DEF}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{8}S_{\triangle ABC}=\frac{3}{8}S_{\triangle ABC}$,
∴$S_{\triangle ABC}=\frac{8}{3}S_{阴影部分}=\frac{8}{3}×6=16$,故选 D.
4 [2025辽宁鞍山质检,中]如图,已知$\triangle ABC$的面积为1,分别倍长(延长一倍)边$AB$,$BC$,$CA得到\triangle A_1B_1C_1$,再分别倍长边$A_1B_1$,$B_1C_1$,$C_1A_1得到\triangle A_2B_2C_2$,…,按此规律,倍长2024次后得到的$\triangle A_{2024}B_{2024}C_{2024}$的面积为 ( )
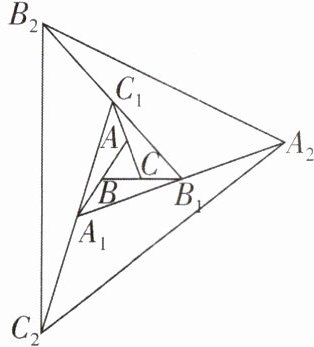
A.$7^{2024}$
B.$5^{2024}$
C.$6^{2023}$
D.$4^{2023}$

A.$7^{2024}$
B.$5^{2024}$
C.$6^{2023}$
D.$4^{2023}$
答案:
A 【解析】如图,连接 AB₁,BC₁,CA₁,根据等底同高的三角形面积相等,可得△A₁BC,△A₁B₁C,△AB₁C,△AB₁C₁,△ABC₁,△A₁BC₁,△ABC 的面积都相等,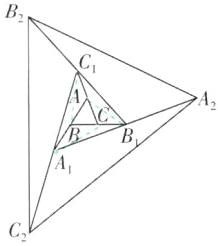
∴$S_{\triangle A₁B₁C₁}=7S_{\triangle ABC}$,同理可得$S_{\triangle A₂B₂C₂}=7S_{\triangle A₁B₁C₁}=7²S_{\triangle ABC}$,…,则$S_{\triangle A_{2024}B_{2024}C_{2024}}=7^{2024}S_{\triangle ABC}$.
∵$S_{\triangle ABC}=1$,
∴△A₂₀₂₄B₂₀₂₄C₂₀₂₄的面积为$7^{2024}$. 故选 A.
A 【解析】如图,连接 AB₁,BC₁,CA₁,根据等底同高的三角形面积相等,可得△A₁BC,△A₁B₁C,△AB₁C,△AB₁C₁,△ABC₁,△A₁BC₁,△ABC 的面积都相等,

∴$S_{\triangle A₁B₁C₁}=7S_{\triangle ABC}$,同理可得$S_{\triangle A₂B₂C₂}=7S_{\triangle A₁B₁C₁}=7²S_{\triangle ABC}$,…,则$S_{\triangle A_{2024}B_{2024}C_{2024}}=7^{2024}S_{\triangle ABC}$.
∵$S_{\triangle ABC}=1$,
∴△A₂₀₂₄B₂₀₂₄C₂₀₂₄的面积为$7^{2024}$. 故选 A.
5 [2025江西景德镇质检,中]如图,$\triangle ABC的三条中线AD$,$BE$,$CF交于点G$.若$AG:GD= 2:1$,$S_{\triangle ABC}= 12$,则图中阴影部分的面积为

4
.
答案:
4 【解析】
∵AD 是△ABC 的中线,
∴$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×12=6$.
∵AG:GD=2:1,
∴$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{2}{3}×6=4$,$S_{\triangle AGC}=\frac{2}{3}S_{\triangle ACD}=\frac{2}{3}×6=4$.又
∵BE,CF 是△ABC 的中线,
∴点 E,F 分别是 AC,AB 的中点,
∴$S_{\triangle GFB}=\frac{1}{2}S_{\triangle ABG}=\frac{1}{2}×4=2$,$S_{\triangle GCE}=\frac{1}{2}S_{\triangle AGC}=\frac{1}{2}×4=2$,
∴$S_{阴影}=S_{\triangle GFB}+S_{\triangle GCE}=2+2=4$. 故答案为 4.
∵AD 是△ABC 的中线,
∴$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×12=6$.
∵AG:GD=2:1,
∴$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{2}{3}×6=4$,$S_{\triangle AGC}=\frac{2}{3}S_{\triangle ACD}=\frac{2}{3}×6=4$.又
∵BE,CF 是△ABC 的中线,
∴点 E,F 分别是 AC,AB 的中点,
∴$S_{\triangle GFB}=\frac{1}{2}S_{\triangle ABG}=\frac{1}{2}×4=2$,$S_{\triangle GCE}=\frac{1}{2}S_{\triangle AGC}=\frac{1}{2}×4=2$,
∴$S_{阴影}=S_{\triangle GFB}+S_{\triangle GCE}=2+2=4$. 故答案为 4.
(1)如图(1),$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$CD是AB$边上的高,则$S_{\triangle ABC}= \frac{1}{2}AC\cdot BC= $
(2)在(1)的条件下,若$AC= 3$,$BC= 4$,$AB= 5$,用等积法求$CD$的长.
(3)如图(2),在等腰三角形$ABC$中,$AB= AC= 13$,$BC= 10$,过$A作AH\perp BC于点H$,且$AH= 12$,$P为底边BC$上的任意一点,过点$P作PM\perp AB$,$PN\perp AC$,垂足分别为$M$,$N$,连接$AP$,利用$S_{\triangle ABC}= S_{\triangle ABP}+S_{\triangle ACP}$,求$PM+PN$的值.
$\frac{1}{2}AB\cdot CD$
.(2)在(1)的条件下,若$AC= 3$,$BC= 4$,$AB= 5$,用等积法求$CD$的长.
【解】由(1)可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,则$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$,解得$CD=\frac{12}{5}$.
(3)如图(2),在等腰三角形$ABC$中,$AB= AC= 13$,$BC= 10$,过$A作AH\perp BC于点H$,且$AH= 12$,$P为底边BC$上的任意一点,过点$P作PM\perp AB$,$PN\perp AC$,垂足分别为$M$,$N$,连接$AP$,利用$S_{\triangle ABC}= S_{\triangle ABP}+S_{\triangle ACP}$,求$PM+PN$的值.
【解】∵AH⊥BC,PM⊥AB,PN⊥AC,$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,∴$\frac{1}{2}BC\cdot AH=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN$,∴$\frac{1}{2}×10×12=\frac{1}{2}×13PM+\frac{1}{2}×13PN=\frac{1}{2}×13(PM+PN)$,∴$PM+PN=\frac{120}{13}$.
答案:
【解】
(1)$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$. 故答案为$\frac{1}{2}AB\cdot CD$.
(2)由
(1)可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,则$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$,解得$CD=\frac{12}{5}$.
(3)
∵AH⊥BC,PM⊥AB,PN⊥AC,$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,
∴$\frac{1}{2}BC\cdot AH=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN$,
∴$\frac{1}{2}×10×12=\frac{1}{2}×13PM+\frac{1}{2}×13PN=\frac{1}{2}×13(PM+PN)$,
∴$PM+PN=\frac{120}{13}$.
(1)$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$. 故答案为$\frac{1}{2}AB\cdot CD$.
(2)由
(1)可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,则$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$,解得$CD=\frac{12}{5}$.
(3)
∵AH⊥BC,PM⊥AB,PN⊥AC,$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,
∴$\frac{1}{2}BC\cdot AH=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN$,
∴$\frac{1}{2}×10×12=\frac{1}{2}×13PM+\frac{1}{2}×13PN=\frac{1}{2}×13(PM+PN)$,
∴$PM+PN=\frac{120}{13}$.
7 [2025吉林松原质检,中]已知$\triangle ABC$的面积为24,$AD是BC$边上的高(点$D不与点B$重合),若$AD= 4$,$CD= 5$,则$BD$的长为 ( )
A.1
B.1或11
C.7
D.7或17
A.1
B.1或11
C.7
D.7或17
答案:
D 【解析】当 AD 在△ABC 内部时,如图
(1).
∵△ABC 的面积为 24,AD 是 BC 边上的高,AD=4,CD=5,
∴$\frac{1}{2}BC\cdot AD=\frac{1}{2}(BD+CD)\cdot AD=\frac{1}{2}(BD+5)×4=24$,
∴BD=7.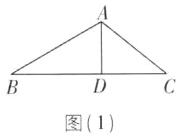
当 AD 在△ABC 外部时,如图
(2).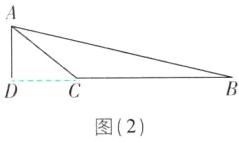
∵△ABC 的面积为 24,AD 是 BC 边上的高,AD=4,CD=5,
∴$\frac{1}{2}BC\cdot AD=\frac{1}{2}BC×4=24$,
∴BC=12,
∴BD=BC+CD=12+5=17. 综上所述,BD 的长为 7 或 17,故选 D.
D 【解析】当 AD 在△ABC 内部时,如图
(1).
∵△ABC 的面积为 24,AD 是 BC 边上的高,AD=4,CD=5,
∴$\frac{1}{2}BC\cdot AD=\frac{1}{2}(BD+CD)\cdot AD=\frac{1}{2}(BD+5)×4=24$,
∴BD=7.

当 AD 在△ABC 外部时,如图
(2).

∵△ABC 的面积为 24,AD 是 BC 边上的高,AD=4,CD=5,
∴$\frac{1}{2}BC\cdot AD=\frac{1}{2}BC×4=24$,
∴BC=12,
∴BD=BC+CD=12+5=17. 综上所述,BD 的长为 7 或 17,故选 D.
查看更多完整答案,请扫码查看


