《2025年初中必刷题八年级数学上册苏科版》

6[中]【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来：
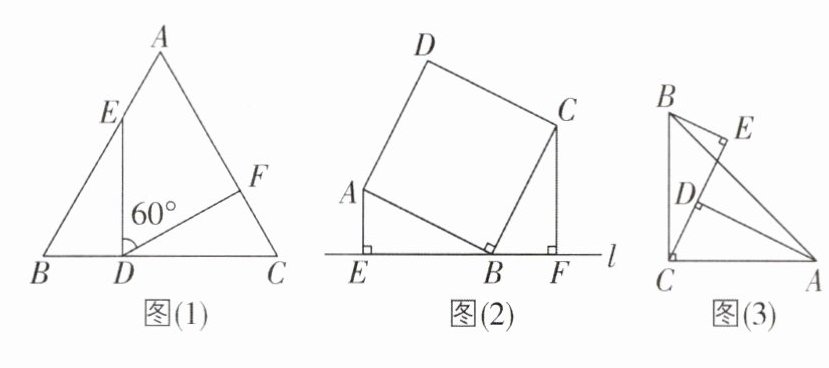
(1)如图(1),$\triangle ABC$为等边三角形,$BD= CF$,$∠EDF= 60^{\circ }$,则$\triangle BDE\cong $____△CFD。
【模型应用】(2)如图(2),正方形ABCD的顶点B在直线l上,分别过点A,C作$AE⊥l$于E,$CF⊥l$于F。若$AE= 1$,$CF= 2$,则EF的长为____3。
【模型变式】(3)如图(3)所示,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,$AC= BC$,$BE⊥CE$于E,$AD⊥CE$于D,$DE= 4cm$,$AD= 6cm$,求BE的长。


【解】因为AD⊥CE，BE⊥CE，所以∠ADC=∠BEC=90°.因为∠DCA+∠BCE=90°，∠DCA+∠DAC=90°，所以∠DAC=∠BCE.又因为AC=BC，所以△ACD≌△CBE(AAS)，所以CE=AD=6cm，CD=BE，所以BE=CD=CE - DE=6 - 4=2(cm).

答案： 【解】
(1)因为△ABC是等边三角形，所以∠B=∠C=60°.因为∠EDC=∠B+∠BED=∠EDF+∠FDC，∠EDF=60°，所以∠BED=∠FDC.又因为BD=CF，所以△BDE≌△CFD(AAS).故答案为△CFD.
(2)因为四边形ABCD是正方形，所以AB=BC，∠ABC=90°.因为AE⊥EF，CF⊥EF，所以∠AEB=∠CFB=90°=∠ABC，所以∠ABE+∠BAE=90°=∠ABE+∠CBF，所以∠BAE=∠CBF，所以△ABE≌△BCF(AAS)，所以AE=BF=1，BE=CF=2，所以EF=3.故答案为3.
(3)因为AD⊥CE，BE⊥CE，所以∠ADC=∠BEC=90°.因为∠DCA+∠BCE=90°，∠DCA+∠DAC=90°，所以∠DAC=∠BCE.又因为AC=BC，所以△ACD≌△CBE(AAS)，所以CE=AD=6cm，CD=BE，所以BE=CD=CE - DE=6 - 4=2(cm).

7[中]【问题背景】如图(1),在四边形ABCD中,$AB= AD$,$∠BAD= 120^{\circ }$,$∠B= ∠ADC= 90^{\circ }$,E,F分别是BC,CD上的点,且$∠EAF= 60^{\circ }$,试探究图中线段BE,EF,FD之间的数量关系。
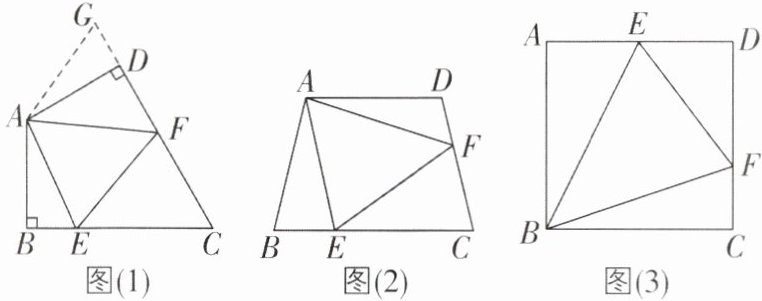
(1)小王同学探究此问题的方法如下：延长FD到点G,使$DG= BE$,连接AG,先证明$\triangle ABE\cong \triangle ADG$,再证明$\triangle AEF\cong \triangle AGF$,可得出结论,他的结论应是____。
【探索延伸】(2)如图(2),若在四边形ABCD中,$AB= AD$,$∠B+∠D= 180^{\circ }$,E,F分别是BC,CD上的点,且$∠EAF= \frac {1}{2}∠BAD$,上述结论是否仍然成立？请说明理由。
【学以致用】(3)如图(3),四边形ABCD是边长为5的正方形,$∠EBF= 45^{\circ }$,直接写出$\triangle DEF$的周长。
 

答案：
【解】
(1)在△ABE和△ADG中，{BE=DG，∠B=∠ADG，AB=AD}，所以△ABE≌△ADG(SAS)，所以AE=AG，∠BAE=∠DAG.因为∠EAF=$\frac{1}{2}$∠BAD，所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD - ∠EAF=∠EAF，所以∠EAF=∠GAF.在△AEF和△AGF中，{AE=AG，∠EAF=∠GAF，AF=AF}，所以△AEF≌△AGF(SAS)，所以EF=FG.因为FG=DG+DF=BE+DF，所以EF=BE+DF.故答案为EF=BE+DF.
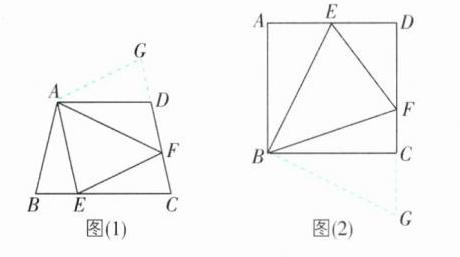
(2)结论EF=BE+DF仍然成立.理由：如图
(1)，延长FD到点G，使DG=BE，连接AG.因为∠B+∠CDA=180°，∠ADG+∠CDA=180°，所以∠B=∠ADG.在△ABE和△ADG中，{BE=DG，∠B=∠ADG，AB=AD}，所以△ABE≌△ADG(SAS)，所以AE=AG，∠BAE=∠DAG.因为∠EAF=$\frac{1}{2}$∠BAD，所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD - ∠EAF=∠EAF，所以∠EAF=∠GAF.在△AEF和△AGF中，{AE=AG，∠EAF=∠GAF，AF=AF}，所以△AEF≌△AGF(SAS)，所以EF=FG.因为FG=DG+DF=BE+DF，所以EF=BE+DF.
(3)△DEF的周长是10.如图
(2)，延长DC到点G，使CG=AE，连接BG.因为四边形ABCD是正方形，所以∠A=∠ABC=∠BCD=90°，AB=BC，所以∠BCG=90°.在△AEB与△CGB中，{AE=CG，∠A=∠BCG，AB=CB}，所以△AEB≌△CGB(SAS)，所以BE=BG，∠ABE=∠CBG.因为∠EBF=45°，∠ABC=90°，所以∠ABE+∠CBF=45°，所以∠CBF+∠CBG=45°.在△EBF与△GBF中，{BE=BG，∠EBF=∠GBF，BF=BF}，所以△EBF≌△GBF(SAS)，所以EF=GF，所以△DEF的周长为EF+ED+DF=AE+CF+DE+DF=AD+CD=5+5=10.