《2025年初中必刷题八年级数学上册苏科版》

1 如图,在单位长度为1的正方形组成3×4的网格图中有a,b,c,d四条线段,下列能作为一个直角三角形三边的线段是(A)
A.a,b,c
B.b,c,d
C.a,b,d
D.a,c,d

答案： 1.A [解析]由题意得$a^{2}=2$，$b^{2}=8$，$c^{2}=10$，$d^{2}=17$。$\because a^{2}+b^{2}=10=c^{2}$，$\therefore a$，$b$，$c$能作为直角三角形的三边。故选A。

2 用三张正方形纸片,按如图所示方式构成图案,若要使所围成的三角形(阴影部分)是直角三角形,则选取的三个正方形纸片的面积不可以是(C)
A.1,2,3
B.2,2,4
C.3,4,5
D.2,3,5

答案： 2.C [解析]由题意可得，三角形各边长的平方是对应的各个正方形的面积。$\because$所围成的三角形是直角三角形，$\therefore$斜边对应的正方形的面积等于两直角边对应的正方形的面积和。又$\because 1 + 2 = 3$，$2 + 2 = 4$，$3 + 4\neq 5$，$2 + 3 = 5$，$\therefore$选取的三个正方形纸片的面积不可以是3，4，5。故选C。

如图,在四边形ABCD中,AB= AD= 6,∠A= 60°,BC= 10,CD= 8,则∠ADC的度数为(C)
A.110°
B.120°
C.150°
D.160°

答案： 3.C [解析]连接BD。$\because AB = AD = 6$，$\angle A = 60^{\circ}$，$\therefore \triangle ABD$是等边三角形，$\therefore BD = 6$，$\angle ADB = 60^{\circ}$。$\because BC = 10$，$CD = 8$，$\therefore BD^{2}+CD^{2}=6^{2}+8^{2}=100$，$BC^{2}=10^{2}=100$，$\therefore BD^{2}+CD^{2}=BC^{2}$，$\therefore \triangle BDC$是直角三角形，$\angle BDC = 90^{\circ}$，$\therefore \angle ADC=\angle ADB+\angle BDC = 150^{\circ}$。故选C。

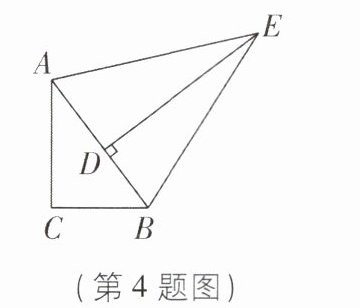
4 [2024江苏无锡梁溪区期中]如图所示,在△ABC中,AC= 8,BC= 6,在△ABE中,DE为AB上的高,DE= 12,S_{△ABE}= 60,则△ABC的面积是______。


24

答案： 4.24 [解析]$\because DE = 12$，$S_{\triangle ABE}=\frac{1}{2}DE\cdot AB = 60$，$\therefore AB = 10$。$\because AC = 8$，$BC = 6$，$6^{2}+8^{2}=10^{2}$，$\therefore AC^{2}+BC^{2}=AB^{2}$，$\therefore \triangle ABC$是直角三角形，$\angle C = 90^{\circ}$，$\therefore S_{\triangle ABC}=\frac{1}{2}AC\cdot BC = 24$。故答案为24。

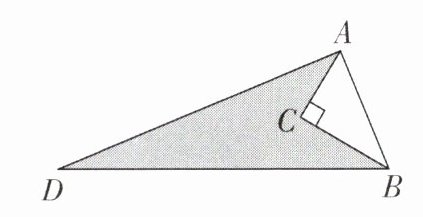
5 如图,△ABD内有一点C,∠ACB= 90°。已知AC= 3cm,BC= 4cm,AD= 12cm,DB= 13cm,则图中阴影部分的面积S= ______。

24cm²

答案： 5.$24\ \text{cm}^2$ [解析]因为$\angle ACB = 90^{\circ}$，由勾股定理得$AB^{2}=AC^{2}+BC^{2}$，即$AB^{2}=3^{2}+4^{2}=25$，所以$AB = 5\ \text{cm}$。在$\triangle ABD$中，因为$AB^{2}+AD^{2}=5^{2}+12^{2}=25 + 144 = 169 = BD^{2}$，所以$\triangle ABD$是直角三角形，$\angle BAD = 90^{\circ}$，所以$S = S_{\triangle ABD}-S_{\triangle ABC}=\frac{1}{2}AB\cdot AD-\frac{1}{2}AC\cdot BC=\frac{1}{2}×5×12-\frac{1}{2}×3×4 = 24(\text{cm}^2)$，故答案为$24\ \text{cm}^2$。

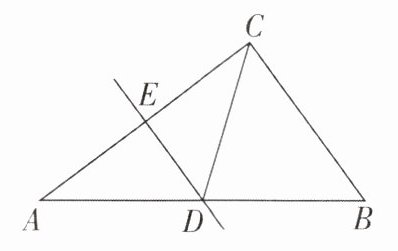
6 如图,已知△ABC中,AB= 10,AC= 8,BC= 6,AC的垂直平分线交AB于点D,垂足为E,连接CD,则CD的长为5。

答案： 6.5 [解析]$\because AB = 10$，$AC = 8$，$BC = 6$，$\therefore BC^{2}+AC^{2}=AB^{2}$，$\therefore \triangle ABC$是直角三角形，$\angle ACB = 90^{\circ}$。$\because DE$是AC的垂直平分线，$\therefore AD = CD$，$\therefore \angle A = \angle ACD$。又$\because \angle A+\angle B = 90^{\circ}$，$\angle ACD+\angle BCD = 90^{\circ}$，$\therefore \angle B = \angle BCD$，$\therefore CD = DB$，$\therefore AD = CD = DB=\frac{1}{2}AB = 5$。故答案为5。

7 [2025江苏南京期中]下面各组数中,是勾股数的是(C)
A.$\sqrt{3}$,2,7
B.0.6,0.8,1
C.3,4,5
D.5,8,10

答案： 7.C [解析]$(\sqrt{3})^{2}+2^{2}\neq7^{2}$，且$\sqrt{3}$不是正整数，故选项A中的数不是勾股数；$0.6^{2}+0.8^{2}=1^{2}$，但0.6，0.8不是正整数，故选项B中的数不是勾股数；$3^{2}+4^{2}=5^{2}$，且3，4，5是正整数，故选项C中的数是勾股数；$5^{2}+8^{2}\neq10^{2}$，故选项D中的数不是勾股数。故选C。

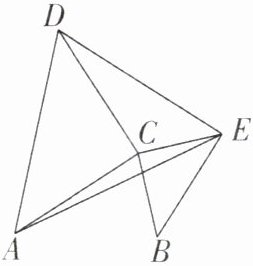
8 [2025吉林长春期末]如图,△ACD和△BCE均为等腰直角三角形,∠ACD= ∠ECB= 90°。连接AE,DE。若$AE^2= DE^2+2CE^2,$求∠DEC的度数。

答案：
8.[解]连接DB，如图。因为$\triangle ACD$和$\triangle ECB$都是等腰直角三角形，$\angle ACD=\angle ECB = 90^{\circ}$，所以$AC = CD$，$CE = CB$，$\angle ACE=\angle DCB$。在$\triangle ACE$和$\triangle DCB$中，$\left\{\begin{array}{l} AC = CD\\ \angle ACE=\angle DCB\\ CE = CB\end{array}\right.$，所以$\triangle ACE\cong\triangle DCB(\text{SAS})$，所以$AE = BD$。因为$\triangle BCE$是等腰直角三角形，$\angle BCE = 90^{\circ}$，所以$\angle BEC=\angle EBC = 45^{\circ}$。在$\text{Rt}\triangle BCE$中，$CE^{2}+CB^{2}=BE^{2}$，所以$BE^{2}=2CE^{2}$。因为$AE^{2}=DE^{2}+2CE^{2}$，所以$BD^{2}=DE^{2}+BE^{2}$，所以$\angle BED = 90^{\circ}$，所以$\angle DEC=\angle BED-\angle BEC = 90^{\circ}-45^{\circ}=45^{\circ}$。

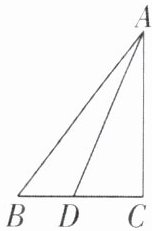
9 [2025江苏常州期中]如图,△ADC中,AD= 13cm,AC= 12cm,DC= 5cm,B是CD延长线上的点,连接AB,AB= 15cm。
(1)试说明∠ACB为直角；
(2)求BD的长。

答案： 9.[解]
(1)$\because AC^{2}+DC^{2}=12^{2}+5^{2}=169$，$AD^{2}=13^{2}=169$，$\therefore AC^{2}+DC^{2}=AD^{2}$，$\therefore \angle ACB = 90^{\circ}$，即$\angle ACB$为直角。
(2)$\because \angle ACB = 90^{\circ}$，$AC = 12\ \text{cm}$，$AB = 15\ \text{cm}$，$\therefore BC^{2}=AB^{2}-AC^{2}=15^{2}-12^{2}=81$，$\therefore BC = 9\ \text{cm}$，$\therefore BD = BC - CD = 9 - 5 = 4(\text{cm})$。