《2025年初中必刷题八年级数学上册苏科版》

10 如图,$\triangle ABC$中,点$D$,$E在边BC$上,$AC= AE= BE= ED$,$\angle DAC= 27^{\circ}$,则$\angle B= $21°。

答案： 21° 【解析】设∠B=x.
∵ AE=BE，
∴ ∠BAE=∠B=x，
∴ ∠AEC=∠BAE+∠B=2x.
∵ AC=AE，
∴ ∠AEC=∠C=2x，
∴ ∠ADE=∠C+∠DAC=2x+27°.
∵ AE=ED，
∴ ∠DAE=∠ADE=2x+27°.在△ADE 中，∠AED+∠DAE+∠ADE=180°，
∴ 2x+2x+27°+2x+27°=180°，
∴ x=21°，
∴ ∠B=21°.故答案为 21°.

11 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为____。

答案：
36°或 45° 【解析】如图（1），△ABC 中，AB=AC，BD=AD，AC=CD，
∴ ∠ABC=∠C=∠BAD，∠CDA=∠CAD，
∴ ∠CDA=2∠ABC，
∴ ∠CAB=3∠ABC.
∵ ∠BAC+∠B+∠C=180°，
∴ 5∠ABC=180°，
∴ ∠ABC=36°.如图（2），△ABC 中，AB=AC，AD=BD=CD，
∴ ∠B=∠C=∠DAC=∠DAB，
∴ ∠BAC=2∠ABC.
∵ ∠BAC+∠B+∠C=180°，
∴ 4∠ABC=180°，
∴ ∠ABC=45°.故答案为 36°或 45°.

12 如图,$\triangle ABD$,$\triangle AEC$都是等边三角形,$DC与BE交于点O$,则$\angle BOC$的度数是120°。

答案： 120° 【解析】
∵ △ABD，△AEC 都是等边三角形，
∴ AD=AB，AE=AC，∠DAB=∠CAE=∠ADB=∠DBA=60°，
∴ ∠DAB+∠BAC=∠CAE+∠BAC，
∴ ∠DAC=∠BAE，
∴ △DAC≌△BAE（SAS），
∴ ∠ADC=∠ABE，
∴ ∠BOC=∠BDO+∠DBA+∠ABE=∠BDO+∠DBA+∠ADC=∠ADB+∠DBA=60°+60°=120°，
∴ ∠BOC 的度数是 120°.

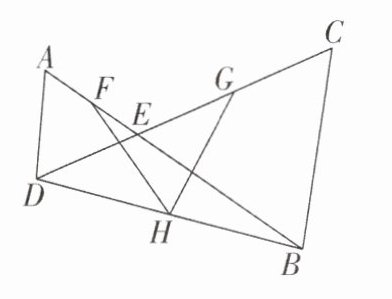
13 [2024江苏镇江质检]如图,$AB$,$CD相交于点E$,$AD= DE$,$BC= BE$,$F$,$G$,$H分别为AE$,$CE$,$BD$的中点,$\angle A= \alpha$,则$\angle FHG= $180° - 2α。(用含$\alpha$的代数式表示)

答案： 180° - 2α 【解析】连接 DF，BG，
∵ DA=DE，BE=BC，AF=EF，EG=CG，
∴ DF⊥AE，BG⊥EC，
∴ ∠DFB=∠DGB=90°.
∵ DH=BH，
∴ FH=DH=BH=GH，
∴ ∠HFB=∠HBF，∠HDG=∠HGD.
∵ DA=DE，
∴ ∠DEA=α.
∵ ∠AED=∠EDB+∠EBD，
∴ ∠EDB+∠EBD=α，
∴ ∠FHG=180° - ∠FHD - ∠GHB=180° - 2∠HBF - 2∠HDG=180° - 2α，故答案为 180° - 2α.

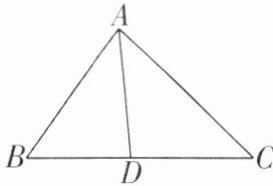
14 [2025河南安阳期末]如图,在$\triangle ABC$中,$\angle BAC的平分线交BC于点D$。
(1)尺规作图：在$AC上求作一点E$,使$\angle ADE= \angle ADB$(不要求写作法,保留作图痕迹),作图依据是____(填“SSS”,“SAS”,“ASA”或“AAS”)。
(2)在(1)的条件下,求证：$\triangle ABD\cong\triangle AED$。
(3)在(1)的条件下,已知$AB= 9$,$\triangle CDE的周长为15$,求$\triangle ABC$的周长。

答案：

(1)【解】如图，点 E 即为所求作，作图依据是 SSS.故答案为 SSS.

(2)【证明】
∵ AD 平分∠BAC，
∴ ∠DAB=∠DAE.在△ABD 和△AED 中，{∠DAB=∠DAE，AD=AD，∠ADB=∠ADE}，
∴ △ABD≌△AED（ASA）.
(3)【解】由（2）可知△ABD≌△AED，
∴ BD=DE，AB=AE=9.
∵ △CDE 的周长为 15，
∴ CD+DE+CE=15，
∴ CD+BD+CE=BC+CE=15，
∴ △ABC 的周长为 AB+BC+CE+AE=9+15+9=33.

15 [2024江苏南京鼓楼区期中]如图,$\triangle ABE$,$\triangle ACD$都是等边三角形,且$B$,$E$,$C$三点在同一条直线上。
(1)求$\angle AED$的度数；
(2)若点$M$,$N分别是线段BC和DE$的中点,连接$AM$,$MN$,$NA$,试判断$\triangle AMN$的形状,并说明理由。

答案： 【解】
(1)
∵ △ABE，△ACD 都是等边三角形，
∴ AB=AE，AD=AC，∠ABC=∠BAE=∠CAD=60°，
∴ ∠BAC=∠EAD.在△ABC 和△AED 中，{AB=AE，∠BAC=∠EAD，AC=AD}，
∴ △ABC≌△AED（SAS），
∴ ∠AED=∠ABC=60°.
(2)△AMN 为等边三角形.理由如下：由（1）可知，△ABC≌△AED，
∴ BC=ED，∠B=∠AED.
∵ 点 M，N 分别是线段 BC 和 DE 的中点，
∴ BM=$\frac{1}{2}$BC，EN=$\frac{1}{2}$DE，
∴ BM=EN.在△BAM 与△EAN 中，{AB=AE，∠B=∠AED，BM=EN}，
∴ △BAM≌△EAN（SAS），
∴ ∠BAM=∠EAN，AM=AN.
∵ ∠BAM - ∠EAM=∠EAN - ∠EAM，
∴ ∠BAE=∠MAN=60°，
∴ △AMN 是等边三角形.

16 问题情境：如图(1),$\angle AOB= 90^{\circ}$,$OC平分\angle AOB$,把三角尺的直角顶点落在$OC上的任意一点P$处,并使三角尺的两条直角边分别与$OA$,$OB相交于点E$,$F$。$PE与PF$相等吗？请说明理由。
变式拓展：如图(2),已知$\angle AOB= 120^{\circ}$,$OC平分\angle AOB$,$P是OC$上一点,$\angle EPF= 60^{\circ}$,$PE与OA相交于点E$,$PF与射线OB的反向延长线相交于点F$。试解决下列问题：
①$PE与PF$还相等吗？为什么？
②试判断$OE$,$OF$,$OP$三条线段之间的数量关系,并说明理由。

答案：
【解】问题情境：相等.理由如下：如图（1），过点 P 作 PM⊥OB 于 M，PN⊥OA 于 N.
∵ OC 平分∠AOB，PM⊥OB，PN⊥OA，
∴ PM=PN.
∵ ∠PMO=∠PNO=∠MON=90°，
∴ ∠MPN=360° - 3×90°=90°.
∵ ∠MPN=∠EPF=90°，
∴ ∠MPF=∠NPE.在△PMF 和△PNE 中，{∠PMF=∠PNE，PM=PN，∠MPF=∠NPE}，
∴ △PMF≌△PNE（ASA），
∴ PF=PE.

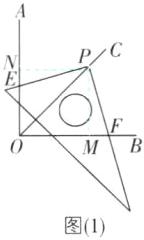
变式拓展：①相等.理由：如图（2），过点 P 作 PM⊥OB 于 M，PN⊥OA 于 N.
∵ OC 平分∠AOB，PM⊥OB，PN⊥OA，
∴ PM=PN.
∵ ∠PMO=∠PNO=90°，∠MON=120°，
∴ ∠MPN=360° - 2×90° - 120°=60°.
∵ ∠MPN=∠EPF=60°，
∴ ∠MPF=∠NPE.在△PMF 和△PNE 中，{∠PMF=∠PNE，PM=PN，∠MPF=∠NPE}，
∴ △PMF≌△PNE（ASA），
∴ PF=PE.②OE - OF=OP.理由：如图（2），在△OPM 和△OPN 中，∠PMO=∠PNO=90°，∠POM=∠PON，
∴ ∠OPM=∠OPN.又
∵ OP=OP，
∴ △POM≌△PON（ASA），
∴ OM=ON.
∵ △PMF≌△PNE，
∴ FM=EN，
∴ OE - OF=EN+ON - (FM - OM)=2OM.在 Rt△OPM 中，∠PMO=90°，∠POM=$\frac{1}{2}$∠AOB=60°，
∴ ∠OPM=30°，
∴ OP=2OM，
∴ OE - OF=OP.