第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 -8 的立方根是(
A.-2
B.2
C.±2
D.不存在
A
)A.-2
B.2
C.±2
D.不存在
答案:
A 【解析】-8 的立方根是$\sqrt [3]{-8}$,即-2。故选 A。
2 [2024 江苏南通调研]若$\sqrt [3]{-6}= x$,则下列等式成立的是(
A.$3x= -6$
B.$x^{3}= -6$
C.$(-x)^{3}= -6$
D.$x= (-6)^{3}$
B
)A.$3x= -6$
B.$x^{3}= -6$
C.$(-x)^{3}= -6$
D.$x= (-6)^{3}$
答案:
B 【解析】$\because \sqrt [3]{-6}=x,\therefore x^{3}=-6$。故选 B。
3 (1)-0.008 的立方根是
-0.2
;(2)216 的立方根是6
;(3)$-3\frac {3}{8}$的立方根是$-\frac {3}{2}$
;(4)$\frac {8}{125}$的立方根是$\frac {2}{5}$
。
答案:
(1)-0.2
(2)6
(3)$-\frac {3}{2}$
(4)$\frac {2}{5}$ 【解析】
(1)$\because (-0.2)^{3}=-0.008$,
∴ -0.008 的立方根为-0.2,即$\sqrt [3]{-0.008}=-0.2$。
(2)$\because 6^{3}=216$,
∴ 216 的立方根为 6,即$\sqrt [3]{216}=6$。
(3)$\because (-\frac {3}{2})^{3}=-3\frac {3}{8}$,
∴$-3\frac {3}{8}$的立方根为$-\frac {3}{2}$,即$\sqrt [3]{-3\frac {3}{8}}=-\frac {3}{2}$。
(4)$\because (\frac {2}{5})^{3}=\frac {8}{125}$,
∴$\frac {8}{125}$的立方根为$\frac {2}{5}$,即$\sqrt [3]{\frac {8}{125}}=\frac {2}{5}$。
(1)-0.2
(2)6
(3)$-\frac {3}{2}$
(4)$\frac {2}{5}$ 【解析】
(1)$\because (-0.2)^{3}=-0.008$,
∴ -0.008 的立方根为-0.2,即$\sqrt [3]{-0.008}=-0.2$。
(2)$\because 6^{3}=216$,
∴ 216 的立方根为 6,即$\sqrt [3]{216}=6$。
(3)$\because (-\frac {3}{2})^{3}=-3\frac {3}{8}$,
∴$-3\frac {3}{8}$的立方根为$-\frac {3}{2}$,即$\sqrt [3]{-3\frac {3}{8}}=-\frac {3}{2}$。
(4)$\because (\frac {2}{5})^{3}=\frac {8}{125}$,
∴$\frac {8}{125}$的立方根为$\frac {2}{5}$,即$\sqrt [3]{\frac {8}{125}}=\frac {2}{5}$。
4 [2024 甘肃兰州城关区期中]平方根、算术平方根、立方根都等于它本身的数是
0
。
答案:
0 【解析】平方根、算术平方根、立方根都等于它本身的数是 0。故答案为 0。
5 [2024 江苏南京质检]已知$5a+2$的立方根是 3,$b^{2}= 16$,则$\sqrt {a-b}= $
1 或 3
。
答案:
1 或 3 【解析】
∵ 5a + 2 的立方根是 3,
∴ 5a + 2 = 27,$\therefore a = 5$。$\because b^{2}=16$,$\therefore b = \pm 4$。当$a = 5$,$b = -4$时,$\sqrt {a - b}=\sqrt {5 + 4}=3$;当$a = 5$,$b = 4$时,$\sqrt {a - b}=\sqrt {5 - 4}=1$。综上,$\sqrt {a - b}$的值为 1 或 3。故答案为 1 或 3。
∵ 5a + 2 的立方根是 3,
∴ 5a + 2 = 27,$\therefore a = 5$。$\because b^{2}=16$,$\therefore b = \pm 4$。当$a = 5$,$b = -4$时,$\sqrt {a - b}=\sqrt {5 + 4}=3$;当$a = 5$,$b = 4$时,$\sqrt {a - b}=\sqrt {5 - 4}=1$。综上,$\sqrt {a - b}$的值为 1 或 3。故答案为 1 或 3。
6 求下列各式中 x 的值。
(1)$x^{3}+2= -214$。
(2)$\frac {1}{2}(2x-1)^{3}= -4$。
(1)$x^{3}+2= -214$。
(2)$\frac {1}{2}(2x-1)^{3}= -4$。
答案:
【解】
(1)$\because x^{3}+2=-214$,$\therefore x^{3}=-216$,$\therefore x=\sqrt [3]{-216}$,即$x = -6$。
(2)$\because \frac {1}{2}(2x - 1)^{3}=-4$,$\therefore (2x - 1)^{3}=-8$,$\therefore 2x - 1=\sqrt [3]{-8}$,即$2x - 1 = -2$,$\therefore x=-\frac {1}{2}$。
(1)$\because x^{3}+2=-214$,$\therefore x^{3}=-216$,$\therefore x=\sqrt [3]{-216}$,即$x = -6$。
(2)$\because \frac {1}{2}(2x - 1)^{3}=-4$,$\therefore (2x - 1)^{3}=-8$,$\therefore 2x - 1=\sqrt [3]{-8}$,即$2x - 1 = -2$,$\therefore x=-\frac {1}{2}$。
7 [2025 江苏南京调研]下列说法正确的是(
A.如果一个数的立方根是这个数本身,那么这个数一定是 0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个不为 0 的数的立方根和这个数同号
D
)A.如果一个数的立方根是这个数本身,那么这个数一定是 0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个不为 0 的数的立方根和这个数同号
答案:
D 【解析】A 选项,如果一个数的立方根是这个数本身,那么这个数一定是 0 或 1 或-1,故错误;B 选项,正数的立方根是正数,负数的立方根是负数,0 的立方根是 0,故错误;C 选项,负数有立方根,故错误;D 选项,一个不为 0 的数的立方根和这个数同号,故正确。故选 D。
8 如果 -b 是 a 的立方根,那么下列结论正确的是(
A.-b 也是 -a 的立方根
B.b 是 a 的立方根
C.b 是 -a 的立方根
D.±b 都是 a 的立方根
C
)A.-b 也是 -a 的立方根
B.b 是 a 的立方根
C.b 是 -a 的立方根
D.±b 都是 a 的立方根
答案:
C 【解析】如果 -b 是 a 的立方根,即$\sqrt [3]{a}=-b$,那么$\sqrt [3]{-a}=b$,即 b 是 -a 的立方根。故选 C。
9 若$\sqrt [3]{a}<-2$,则 a 的值可以是(
A.-9
B.-4
C.4
D.9
A
)A.-9
B.-4
C.4
D.9
答案:
A 【解析】因为$\sqrt [3]{a}<-2$,所以$a<-8$,所以 a 的值可以是-9。故选 A。
10 按照下列程序进行计算,最后输出的答案是(
A.$\sqrt {x^{3}}+2$
B.$\sqrt [3]{x^{2}}+2$
C.$\sqrt [3]{x^{2}+2}$
D.$\sqrt [3]{2x^{2}}$
B
)A.$\sqrt {x^{3}}+2$
B.$\sqrt [3]{x^{2}}+2$
C.$\sqrt [3]{x^{2}+2}$
D.$\sqrt [3]{2x^{2}}$
答案:
B 【解析】根据题意得最后输出的答案是$\sqrt [3]{x^{2}}+2$。故选 B。
11 [2025 江苏南通期末]如图,二阶魔方由 8 个形状大小完全相同的小正方体组成,已知二阶魔方的体积为$48cm^{3}$(每个小正方体之间的缝隙忽略不计),则每个小正方体的棱长为(
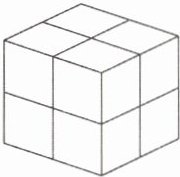
A.$\sqrt [3]{6}cm$
B.$3cm$
C.$\sqrt {6}cm$
D.$2\sqrt {6}cm$
A
)
A.$\sqrt [3]{6}cm$
B.$3cm$
C.$\sqrt {6}cm$
D.$2\sqrt {6}cm$
答案:
A 【解析】根据题意得,每个小正方体的体积为$48÷8 = 6(cm^{3})$,
∴ 每个小正方体的棱长为$\sqrt [3]{6}cm$,故选 A。
∴ 每个小正方体的棱长为$\sqrt [3]{6}cm$,故选 A。
12 [2024 广东汕尾期末]如图为一正方体的表面展开图,将它 折成正方体后,如果相对面对应的值相等,那么 x 的平方与 y 的立方根之和为______。
折成正方体后,如果相对面对应的值相等,那么 x 的平方与 y 的立方根之和为______。
 折成正方体后,如果相对面对应的值相等,那么 x 的平方与 y 的立方根之和为______。
折成正方体后,如果相对面对应的值相等,那么 x 的平方与 y 的立方根之和为______。5
答案:
5 【解析】根据正方体表面展开图的特征可知$x - y$所在面与 1 所在面相对,$x + y$所在面与 3 所在面相对,$\therefore x - y = 1$,$x + y = 3$,$\therefore x = 2$,$y = 1$,$\therefore x^{2}+\sqrt [3]{y}=4 + 1 = 5$,即 x 的平方与 y 的立方根之和为 5。故答案为 5。
13 判断下列说法是否正确。
(1)$\sqrt {64}$的立方根是 -2;
(2)±3 是 27 的立方根。
李蕾认为(1)错误,(2)正确。请问李蕾的观点正确吗?如果不正确,请说明理由。
(1)$\sqrt {64}$的立方根是 -2;
(2)±3 是 27 的立方根。
李蕾认为(1)错误,(2)正确。请问李蕾的观点正确吗?如果不正确,请说明理由。
答案:
【解】李雷的观点错误。理由如下:$\sqrt {64}=8$,8 的立方根为 2,故
(1)错误;3 是 27 的立方根,故
(2)错误。
(1)错误;3 是 27 的立方根,故
(2)错误。
查看更多完整答案,请扫码查看


