第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
如图,在平面直角坐标系中,点 A,B,C 的坐标分别为$(4,6),(4,0),(-2,3)$. 将点 C 向右平移 n 个单位后得到点$C'$. 若点$C'落在\triangle AOB$内(包括边界),则 n 的取值范围是 (
A.$4\leq n\leq6$
B.$4\leq n\leq7$
C.$5\leq n\leq6$
D.$5\leq n\leq7$
A
)A.$4\leq n\leq6$
B.$4\leq n\leq7$
C.$5\leq n\leq6$
D.$5\leq n\leq7$
答案:
A [解析]
∵点A,B的坐标分别为(4,6),(4,0),
∴OA中点和AB中点的坐标分别为(2,3),(4,3).
∵点C的坐标为(-2,3),2 - (-2)=4,4 - (-2)=6,
∴n的取值范围是4≤n≤6.故选A.
∵点A,B的坐标分别为(4,6),(4,0),
∴OA中点和AB中点的坐标分别为(2,3),(4,3).
∵点C的坐标为(-2,3),2 - (-2)=4,4 - (-2)=6,
∴n的取值范围是4≤n≤6.故选A.
在平面直角坐标系中,将$A(1,m^2)$向下平移$(2m^2 + 3)$个单位后得到 B 点. 有四个点$M(1,-m^2 - 4),N(1,-2m^2 - 3),P(1,-m^2),Q(1,-3m^2)$,则一定在线段 AB 上的是 (
A.点 M
B.点 N
C.点 P
D.点 Q
C
)A.点 M
B.点 N
C.点 P
D.点 Q
答案:
C [解析]
∵将A(1,$m^{2}$)向下平移($2m^{2}+3$)个单位后得到B点,
∴B(1,$-m^{2}-3$),
∴线段AB在y轴右侧,且与y轴平行,距离y轴1个单位.
∵$m^{2}\geq0$,
∴$-m^{2}-3\leq-3$.
∵$-m^{2}-4\leq-4$,
∴M(1,$-m^{2}-4$)不在线段AB上.
∵$-2m^{2}-3\leq-3$,
∴当m = 0时,N(1,$-2m^{2}-3$)在线段AB上,当m≠0时,N(1,$-2m^{2}-3$)不在线段AB上.
∵$-m^{2}-3<-m^{2}$,且$m^{2}\geq-m^{2}$,
∴P(1,$-m^{2}$)一定在线段AB上.当$-3m^{2}\geq-m^{2}-3$时,$0\leq m^{2}\leq\frac{3}{2}$,此时Q(1,$-3m^{2}$)在线段AB上.当$-3m^{2}<-m^{2}-3$时,$m^{2}>\frac{3}{2}$,此时Q(1,$-3m^{2}$)不在线段AB上.综上,一定在线段AB上的是点P.故选C.
∵将A(1,$m^{2}$)向下平移($2m^{2}+3$)个单位后得到B点,
∴B(1,$-m^{2}-3$),
∴线段AB在y轴右侧,且与y轴平行,距离y轴1个单位.
∵$m^{2}\geq0$,
∴$-m^{2}-3\leq-3$.
∵$-m^{2}-4\leq-4$,
∴M(1,$-m^{2}-4$)不在线段AB上.
∵$-2m^{2}-3\leq-3$,
∴当m = 0时,N(1,$-2m^{2}-3$)在线段AB上,当m≠0时,N(1,$-2m^{2}-3$)不在线段AB上.
∵$-m^{2}-3<-m^{2}$,且$m^{2}\geq-m^{2}$,
∴P(1,$-m^{2}$)一定在线段AB上.当$-3m^{2}\geq-m^{2}-3$时,$0\leq m^{2}\leq\frac{3}{2}$,此时Q(1,$-3m^{2}$)在线段AB上.当$-3m^{2}<-m^{2}-3$时,$m^{2}>\frac{3}{2}$,此时Q(1,$-3m^{2}$)不在线段AB上.综上,一定在线段AB上的是点P.故选C.
3 [2025 江苏徐州质检,中]如图,在平面直角坐标系中,将正方形①依次平移后得到正方形②,③,④,…;相应地,顶点 A 依次平移后得到$A_1,A_2,A_3,…$,其中点 A 坐标为$(1,0)$,点$A_1坐标为(0,1)$,则点$A_{20}$的坐标为____.
(-19,8)
答案:
(-19,8) [解析]观察题图可知,$A_{3}(-2,1)$,$A_{6}(-5,2)$,$A_{9}(-8,3)$,…
∵ - 2 = 1 - 3×1, - 5 = 1 - 3×2, - 8 = 1 - 3×3,
∴点$A_{18}$的横坐标为1 - 3×6 = - 17,
∴$A_{18}(-17,6)$.把点$A_{18}$向左平移2个单位,再向上平移2个单位得点$A_{20}$,
∴$A_{20}(-19,8)$.故答案为(-19,8).
∵ - 2 = 1 - 3×1, - 5 = 1 - 3×2, - 8 = 1 - 3×3,
∴点$A_{18}$的横坐标为1 - 3×6 = - 17,
∴$A_{18}(-17,6)$.把点$A_{18}$向左平移2个单位,再向上平移2个单位得点$A_{20}$,
∴$A_{20}(-19,8)$.故答案为(-19,8).
4 [中]如图,在平面直角坐标系中,点 A 的坐标为$(2,0)$,点 B 的坐标为$(0,1)$,将线段 AB 平移,使其一个端点到点 C(3,2),则平移后另一端点的坐标为____.


答案:
(1,3)或(5,1) [解析]①如图
(1),当A平移到点C时,
∵C(3,2),点A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增加1,纵坐标增加2,
∴平移后的点B坐标为(1,3);②如图
(2),当B平移到点C时,
∵C(3,2),点A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增加3,纵坐标增加1,
∴平移后的点A的坐标为(5,1).故答案为(1,3)或(5,1).


(1,3)或(5,1) [解析]①如图
(1),当A平移到点C时,
∵C(3,2),点A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增加1,纵坐标增加2,
∴平移后的点B坐标为(1,3);②如图
(2),当B平移到点C时,
∵C(3,2),点A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增加3,纵坐标增加1,
∴平移后的点A的坐标为(5,1).故答案为(1,3)或(5,1).


5 [2025 浙江杭州临平区调研,中]如图,在平面直角坐标系中,有点$A(1,0)$,点$B(-3,0)$,点$C(x,y)$.
(1)若$x = - 2,y = 3$,求$\triangle ABC$的面积.
(2)若$C(x,y)$在第二象限,$CB// y$轴,线段 AC 交 y 轴于点$E(0,1)$.
①判断$\triangle ABC$的形状,并说明理由.
②$\triangle ABC$沿 x 轴正方向平移,使点 B 与原点重合,得到$\triangle FOD$,求四边形 AEDF 的面积.

(1)若$x = - 2,y = 3$,求$\triangle ABC$的面积.
(2)若$C(x,y)$在第二象限,$CB// y$轴,线段 AC 交 y 轴于点$E(0,1)$.
①判断$\triangle ABC$的形状,并说明理由.
②$\triangle ABC$沿 x 轴正方向平移,使点 B 与原点重合,得到$\triangle FOD$,求四边形 AEDF 的面积.

答案:
[解]
(1)
∵A(1,0),B(-3,0),
∴AO = 1,OB = 3,
∴AB = 4.
∵C(-2,3),
∴$S_{\triangle ABC}=\frac{1}{2}×4×3=6$.
(2)①△ABC是等腰直角三角形.理由:
∵E(0,1),A(1,0),
∴OA = OE = 1,
∴∠OAE = ∠OEA = 45°.
∵BC//y轴,
∴∠C = ∠OEA = 45°,
∴∠C = ∠OAE = 45°,
∴BC = BA,∠ABC = 90°,
∴△ABC是等腰直角三角形.
②由①知BC = AB = 4,
∴OD = OF = 4,
∴$S_{四边形AEDF}=S_{\triangle ODF}-S_{\triangle AOE}=\frac{1}{2}×4×4-\frac{1}{2}×1×1=7.5$.
(1)
∵A(1,0),B(-3,0),
∴AO = 1,OB = 3,
∴AB = 4.
∵C(-2,3),
∴$S_{\triangle ABC}=\frac{1}{2}×4×3=6$.
(2)①△ABC是等腰直角三角形.理由:
∵E(0,1),A(1,0),
∴OA = OE = 1,
∴∠OAE = ∠OEA = 45°.
∵BC//y轴,
∴∠C = ∠OEA = 45°,
∴∠C = ∠OAE = 45°,
∴BC = BA,∠ABC = 90°,
∴△ABC是等腰直角三角形.
②由①知BC = AB = 4,
∴OD = OF = 4,
∴$S_{四边形AEDF}=S_{\triangle ODF}-S_{\triangle AOE}=\frac{1}{2}×4×4-\frac{1}{2}×1×1=7.5$.
6 思想方法 数形结合 [2025 江苏南京期末,难][定义]若线段 AB 上所有的点到 x 轴的距离的最大值为 W,W 就叫线段 AB 的界值,记作$W_{AB}$.
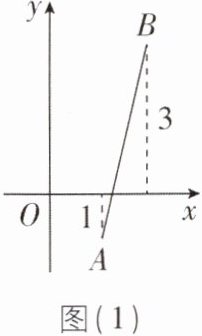
[理解]如图(1),线段 AB 上所有的点到 x 轴的最大距离是 3,则线段 AB 的界值$W_{AB} = 3$.
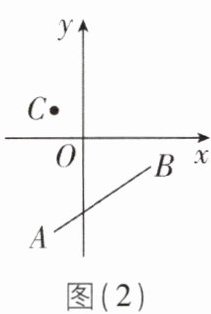
[应用](1)如图(2),已知$A(-1,-3),B(2,-1),C(-1,1)$.
①$W_{AB} = $____.
②平移线段 AB,使点 A 与点 C 重合,平移后线段的界值 W 为____.
[拓展](2)如图(3),$A(-3,-7),B(1,-3)$,将线段 AB 向上平移$m(m > 0)个单位得到线段CD$(C 与 A 为对应点).
①当$5\leq m\leq6$时,$W_{CD}$的取值范围为____.
②当$m > 5$时,用含 m 的式子表示$W_{CD}$.

[答案]:[解](1)①∵A(-1,-3),B(2,-1),∴W$_{AB}$ = 3.故答案为3.
②∵平移线段AB,使点A(-1,-3)与点C(-1,1)重合,∴需将线段AB向上平移4个单位,∴B(2,-1)平移后的对应点的坐标为(2,3),∴平移后线段的界值W为3.故答案为3.
(2)已知A(-3,-7),B(1,-3),将线段AB向上平移m(m > 0)个单位得到线段CD,则C(-3,-7 + m),D(1,-3 + m).
①∵5≤m≤6,∴ - 2≤ - 7 + m≤ - 1,2≤ - 3 + m≤3,∴W$_{CD}$的取值范围为2≤W$_{CD}$≤3.故答案为2≤W$_{CD}$≤3.
②∵m > 5,∴ - 7 + m > - 2, - 3 + m > 2.又∵ - 3 + m > - 7 + m,∴W$_{CD}$ = - 3 + m.
[应用](1)①$W_{AB} = $
②平移线段 AB,使点 A 与点 C 重合,平移后线段的界值 W 为
[拓展](2)如图(3),$A(-3,-7),B(1,-3)$,将线段 AB 向上平移$m(m > 0)个单位得到线段CD$(C 与 A 为对应点).
①当$5\leq m\leq6$时,$W_{CD}$的取值范围为
②当$m > 5$时,用含 m 的式子表示$W_{CD}$.
[理解]如图(1),线段 AB 上所有的点到 x 轴的最大距离是 3,则线段 AB 的界值$W_{AB} = 3$.


[应用](1)如图(2),已知$A(-1,-3),B(2,-1),C(-1,1)$.
①$W_{AB} = $____.
②平移线段 AB,使点 A 与点 C 重合,平移后线段的界值 W 为____.
[拓展](2)如图(3),$A(-3,-7),B(1,-3)$,将线段 AB 向上平移$m(m > 0)个单位得到线段CD$(C 与 A 为对应点).
①当$5\leq m\leq6$时,$W_{CD}$的取值范围为____.
②当$m > 5$时,用含 m 的式子表示$W_{CD}$.

[答案]:[解](1)①∵A(-1,-3),B(2,-1),∴W$_{AB}$ = 3.故答案为3.
②∵平移线段AB,使点A(-1,-3)与点C(-1,1)重合,∴需将线段AB向上平移4个单位,∴B(2,-1)平移后的对应点的坐标为(2,3),∴平移后线段的界值W为3.故答案为3.
(2)已知A(-3,-7),B(1,-3),将线段AB向上平移m(m > 0)个单位得到线段CD,则C(-3,-7 + m),D(1,-3 + m).
①∵5≤m≤6,∴ - 2≤ - 7 + m≤ - 1,2≤ - 3 + m≤3,∴W$_{CD}$的取值范围为2≤W$_{CD}$≤3.故答案为2≤W$_{CD}$≤3.
②∵m > 5,∴ - 7 + m > - 2, - 3 + m > 2.又∵ - 3 + m > - 7 + m,∴W$_{CD}$ = - 3 + m.
[应用](1)①$W_{AB} = $
3
.②平移线段 AB,使点 A 与点 C 重合,平移后线段的界值 W 为
3
.[拓展](2)如图(3),$A(-3,-7),B(1,-3)$,将线段 AB 向上平移$m(m > 0)个单位得到线段CD$(C 与 A 为对应点).
①当$5\leq m\leq6$时,$W_{CD}$的取值范围为
2≤W$_{CD}$≤3
.②当$m > 5$时,用含 m 的式子表示$W_{CD}$.
$W_{CD} = - 3 + m$
答案:
[解]
(1)①
∵A(-1,-3),B(2,-1),
∴W$_{AB}$ = 3.故答案为3.
②
∵平移线段AB,使点A(-1,-3)与点C(-1,1)重合,
∴需将线段AB向上平移4个单位,
∴B(2,-1)平移后的对应点的坐标为(2,3),
∴平移后线段的界值W为3.故答案为3.
(2)已知A(-3,-7),B(1,-3),将线段AB向上平移m(m > 0)个单位得到线段CD,则C(-3,-7 + m),D(1,-3 + m).
①
∵5≤m≤6,
∴ - 2≤ - 7 + m≤ - 1,2≤ - 3 + m≤3,
∴W$_{CD}$的取值范围为2≤W$_{CD}$≤3.故答案为2≤W$_{CD}$≤3.
②
∵m > 5,
∴ - 7 + m > - 2, - 3 + m > 2.又
∵ - 3 + m > - 7 + m,
∴W$_{CD}$ = - 3 + m.
(1)①
∵A(-1,-3),B(2,-1),
∴W$_{AB}$ = 3.故答案为3.
②
∵平移线段AB,使点A(-1,-3)与点C(-1,1)重合,
∴需将线段AB向上平移4个单位,
∴B(2,-1)平移后的对应点的坐标为(2,3),
∴平移后线段的界值W为3.故答案为3.
(2)已知A(-3,-7),B(1,-3),将线段AB向上平移m(m > 0)个单位得到线段CD,则C(-3,-7 + m),D(1,-3 + m).
①
∵5≤m≤6,
∴ - 2≤ - 7 + m≤ - 1,2≤ - 3 + m≤3,
∴W$_{CD}$的取值范围为2≤W$_{CD}$≤3.故答案为2≤W$_{CD}$≤3.
②
∵m > 5,
∴ - 7 + m > - 2, - 3 + m > 2.又
∵ - 3 + m > - 7 + m,
∴W$_{CD}$ = - 3 + m.
查看更多完整答案,请扫码查看


