《2025年初中必刷题八年级数学上册苏科版》

为进一步美化校园,某校计划在校园绿化区增设3条绿化带,如图所示,绿化带MN//PQ,绿化带AB交绿化带MN于A,交绿化带PQ于B.若要修建一喷灌设施,要求其到三条绿化带的距离相等,则可供选择的喷灌设施修建点有(C)
A.4处
B.3处
C.2处
D.1处

答案： C　[解析]
∵MN//PQ,∠BAN和∠ABQ的平分线的交点到AB,MN,PQ距离相等,∠BAM和∠ABP的平分线的交点到AB,MN,PQ距离相等,
∴可供选择的喷灌设施修建点有2处.故选C.

如图,在四边形ABCD中,∠A= 90°,AD= 3,连接BD,BD⊥CD,∠ADB= ∠C.若P是BC边上一动点,则DP长的最小值为(C)
A.1
B.6
C.3
D.2

答案： C　[解析]过点D作DH⊥BC于点H.
∵BD⊥CD,
∴∠BDC=90°.
∵∠C+∠BDC+∠DBC=180°,∠ADB+∠A+∠ABD=180°,∠ADB=∠C,∠A=∠BDC=90°,
∴∠ABD=∠CBD,
∴BD是∠ABC的平分线.又
∵AD⊥AB,DH⊥BC,
∴AD=DH.
∵AD=3,
∴DH=3,
∴当点P运动到与点H重合时,DP长有最小值,即DP长的最小值为3.故选C.

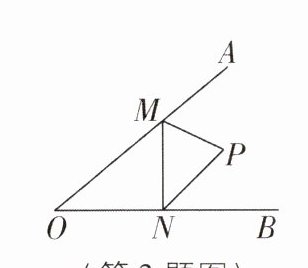
3[2024江苏无锡梁溪区期中,中]如图,在∠AOB的边OA,OB上取点M,N,连接MN,MP平分∠AMN,NP平分∠MNB,若MN= 4,△PMN的面积是6,△OMN的面积是9,则OM+ON的值是______.

答案：
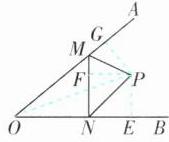
10　[解析]如图,过点P作PE⊥OB,PF⊥MN,PG⊥OA,垂足分别为E,F,G,连接OP.
∵MP平分∠AMN,NP平分∠MNB,
∴PF=PG=PE.
∵MN=4,△PMN的面积是6,
∴$\frac{1}{2}$MN·PF=6,
∴PF=3,
∴PG=PE=3.
∵△OMN的面积是9,
∴△OMP的面积+△ONP的面积=15,
∴$\frac{1}{2}$OM·PG+$\frac{1}{2}$ON·PE=15,
∴OM+ON=10.故答案为10.

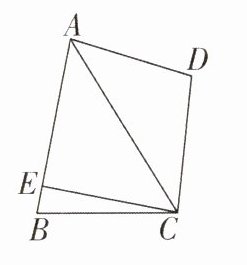
4[2024江苏扬州调研,较难]如图,已知四边形ABCD的对角互补,且∠BAC= ∠DAC,AB= 15,AD= 12.过顶点C作CE⊥AB于E,则AE/BE的值为______.

答案：
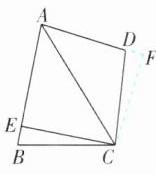
9　[解析]如图,过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°.
∵CE⊥AB,
∴∠CEB=∠CEA=90°,
∴∠CEB=∠CEA=∠CFD.
∵∠BAC=∠DAC,
∴AC平分∠BAD,
∴CE=CF.在△AEC和△AFC中,$\begin{cases} ∠EAC=∠FAC, \\ ∠AEC=∠AFC, \\ CE=CF, \end{cases}$
∴△AEC≌△AFC(AAS),
∴AE=AF.
∵四边形ABCD的对角互补,
∴∠B+∠ADC=180°.
∵∠CDF+∠ADC=180°,
∴∠B=∠CDF.在△CEB和△CFD中,$\begin{cases} ∠CEB=∠F, \\ ∠B=∠CDF, \\ CE=CF, \end{cases}$
∴△CEB≌△CFD(AAS),
∴BE=DF.设BE=DF=a.
∵AB=15,AD=12,
∴12+a=15-a,
∴a=1.5,
∴AE=13.5,BE=1.5,
∴$\frac{AE}{BE}=\frac{13.5}{1.5}=9$,故答案为9.

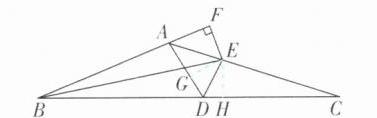
5[较难]如图,△ABC中,点D在BC边上,∠BAD= 100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,交BA的延长线于F,且∠AEF= 50°,连接DE.
(1)求∠CAD的度数.
(2)求证:DE平分∠ADC.
(3)若AB= 7,AD= 4,CD= 8,且S_△ACD= 15,求△ABE的面积.

答案：

(1)[解]
∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°−50°=40°.
∵∠BAD=100°,
∴∠CAD=180°−100°−40°=40°.
(2)[证明]过点E作EG⊥AD于G,EH⊥BC于H,如图.
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH.
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC.
(3)[解]如上图,
∵S△ACD=15,
∴$\frac{1}{2}$AD·EG+$\frac{1}{2}$CD·EH=15,即$\frac{1}{2}$×4×EG+$\frac{1}{2}$×8×EH=15,解得EG=EH=$\frac{5}{2}$,
∴EF=$\frac{5}{2}$,
∴△ABE的面积为$\frac{1}{2}$AB·EF=$\frac{1}{2}$×7×$\frac{5}{2}$=$\frac{35}{4}$.

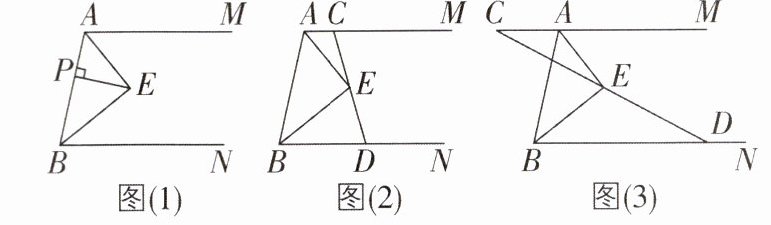
6核心素养模型观念[较难]已知AM//BN,AE平分∠BAM,BE平分∠ABN,∠AEB= 90°.
(1)如图(1),作EP⊥AB,若PE= 3,求点E到AM与BN的距离之和.
(2)如图(2),过点E的直线交射线AM于点C,交射线BN于点D,求证:AC+BD= AB.
(3)如图(3),过点E的直线交射线AM的反向延长线于点C,交射线BN于点D,AB= 5,AC= 3,S_△ABE - S_△ACE= 2,求△BDE的面积.

答案：

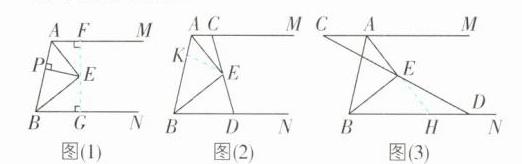
(1)[解]如图
(1),过点E作EF⊥AM于F,作EG⊥BN于G.
∵AE平分∠BAM,PE⊥AB,
∴EF=PE,同理可得EG=PE.
∵AM//BN,
∴易知F,E,G三点共线,
∴FG的长即为点E到AM与BN的距离之和,
∴点E到AM与BN的距离之和为3+3=6.
(2)[证明]如图
(2),在AB上截取AK=AC,连接EK.在△ACE与△AKE中,$\begin{cases} AC=AK, \\ ∠CAE=∠KAE, \\ AE=AE, \end{cases}$
∴△ACE≌△AKE,
∴∠AEC=∠AEK.
∵∠AEB=90°,
∴∠AEK+∠BEK=∠AEC+∠BED=90°,
∴∠KEB=∠DEB.在△BKE与△BDE中,$\begin{cases} ∠KBE=∠DBE, \\ BE=BE, \\ ∠KEB=∠DEB, \end{cases}$
∴△BKE≌△BDE,
∴BK=BD.
∵AB=AK+BK,
∴AC+BD=AB.
(3)[解]如图
(3),延长AE交BD于点H.
∵∠AEB=90°,
∴∠BEH=∠AEB=90°.又
∵BE平分∠ABN,
∴∠ABE=∠HBE.在△ABE和△HBE中,$\begin{cases} ∠AEB=∠HEB, \\ BE=BE, \\ ∠ABE=∠HBE, \end{cases}$
∴△ABE≌△HBE,
∴AB=BH=5,AE=EH,S△ABE=S△HBE.
∵AM//BN,
∴∠C=∠EDH.在△ACE与△HDE中,$\begin{cases} ∠C=∠EDH, \\ ∠AEC=∠HED, \\ AE=HE, \end{cases}$
∴△ACE≌△HDE,
$∴DH=AC=3,S_{△DEH}=S_{△ACE}.$
∵BH=5,DH=3,
$∴设S_{△BEH}=S_{△ABE}=5x,S_{△DEH}=S_{△ACE}=3x.$
$∵S_{△ABE} - S_{△ACE}=2,$
∴5x - 3x=2,
∴x=1,
$∴S_{△BDE}=S_{△BEH}+S_{△DEH}=8.$