第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2024江苏南通中考]“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为5,$(m + n)^2 = 21$,则大正方形面积为(
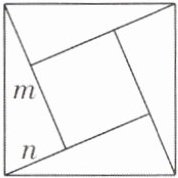
A.12
B.13
C.14
D.15
B
)
A.12
B.13
C.14
D.15
答案:
B【解析】由题意可知,中间小正方形的边长为m - n,
∴(m - n)² = 5,即m² + n² - 2mn = 5.①
∵(m + n)² = 21,
∴m² + n² + 2mn = 21.②① + ②,得2(m² + n²) = 26,
∴m² + n² = 13,
∴大正方形的面积为13,故选B.
∴(m - n)² = 5,即m² + n² - 2mn = 5.①
∵(m + n)² = 21,
∴m² + n² + 2mn = 21.②① + ②,得2(m² + n²) = 26,
∴m² + n² = 13,
∴大正方形的面积为13,故选B.
2 [2024江苏常州中考]如图,在Rt△ABC中,∠ACB= 90°,AC= 6,BC= 4,D是边AC的中点,E是边BC上一点,连接BD,DE.将△CDE沿DE翻折,点C落在BD上的点F处,则CE= ____

$\frac{3}{2}$
.
答案:
$\frac{3}{2}$【解析】
∵∠ACB = 90°,AC = 6,BC = 4,D是边AC的中点,
∴CD = $\frac{1}{2}$AC = 3,
∴BD = $\sqrt{BC² + CD²}$ = 5.
∵将△CDE沿DE翻折,点C落在BD上的点F处,
∴CD = DF = 3,CE = EF,∠EFD = 90°,
∴BF = BD - DF = 2,∠BFE = 90°.设CE = x,则EF = x,BE = BC - CE = 4 - x.在Rt△BFE中,由勾股定理,得(4 - x)² = x² + 2²,解得x = $\frac{3}{2}$,
∴CE = $\frac{3}{2}$.故答案为$\frac{3}{2}$.
∵∠ACB = 90°,AC = 6,BC = 4,D是边AC的中点,
∴CD = $\frac{1}{2}$AC = 3,
∴BD = $\sqrt{BC² + CD²}$ = 5.
∵将△CDE沿DE翻折,点C落在BD上的点F处,
∴CD = DF = 3,CE = EF,∠EFD = 90°,
∴BF = BD - DF = 2,∠BFE = 90°.设CE = x,则EF = x,BE = BC - CE = 4 - x.在Rt△BFE中,由勾股定理,得(4 - x)² = x² + 2²,解得x = $\frac{3}{2}$,
∴CE = $\frac{3}{2}$.故答案为$\frac{3}{2}$.
3 [2024陕西中考]如图,在△ABC中,AB= AC,E是边AB上一点,连接CE,在BC的右侧作BF//AC,且BF= AE,连接CF.若AC= 13,BC= 10,则四边形EBFC的面积为____.
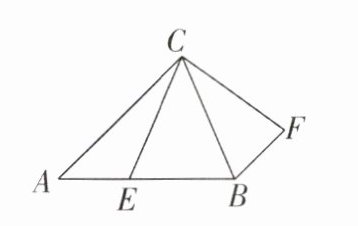

答案:
60【解析】
∵AB = AC,
∴∠ABC = ∠ACB.
∵BF//AC,
∴∠ACB = ∠CBF,
∴∠ABC = ∠CBF,
∴BC平分∠ABF.如图,过点C作CM⊥AB于点M,CN⊥BF于点N,则CM = CN.
∵S△ACE = $\frac{1}{2}$AE·CM,S△CBF = $\frac{1}{2}$BF·CN,且BF = AE,
∴S△CBF = S△ACE,
∴四边形EBFC的面积为S△CBF + S△CBE = S△ACE + S△CBE = S△CBA.
∵AC = 13,
∴AB = 13.设AM = x,则BM = 13 - x.由勾股定理,得CM² = AC² - AM² = BC² - BM²,
∴13² - x² = 10² - (13 - x)²,解得x = $\frac{119}{13}$,
∴CM = $\sqrt{13² - (\frac{119}{13})²}$ = $\frac{120}{13}$,
∴S△CBA = $\frac{1}{2}$AB·CM = 60,
∴四边形EBFC的面积为60.故答案为60.

60【解析】
∵AB = AC,
∴∠ABC = ∠ACB.
∵BF//AC,
∴∠ACB = ∠CBF,
∴∠ABC = ∠CBF,
∴BC平分∠ABF.如图,过点C作CM⊥AB于点M,CN⊥BF于点N,则CM = CN.
∵S△ACE = $\frac{1}{2}$AE·CM,S△CBF = $\frac{1}{2}$BF·CN,且BF = AE,
∴S△CBF = S△ACE,
∴四边形EBFC的面积为S△CBF + S△CBE = S△ACE + S△CBE = S△CBA.
∵AC = 13,
∴AB = 13.设AM = x,则BM = 13 - x.由勾股定理,得CM² = AC² - AM² = BC² - BM²,
∴13² - x² = 10² - (13 - x)²,解得x = $\frac{119}{13}$,
∴CM = $\sqrt{13² - (\frac{119}{13})²}$ = $\frac{120}{13}$,
∴S△CBA = $\frac{1}{2}$AB·CM = 60,
∴四边形EBFC的面积为60.故答案为60.

4 [2024黑龙江大庆中考]如图(1),直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图(2)是1次操作后的图形.图(3)是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图(1)中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为____.
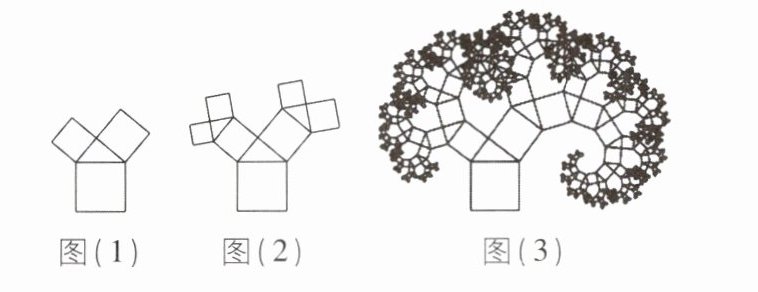

答案:
48【解析】把题图
(2)中各个小正方形标上字母,如图.设正方形a的边长为x,正方形b的边长为y,
∴正方形a的面积为x²,正方形b的面积为y².由题意得正方形c的边长为2,并且其中一条边是直角三角形的斜边,
∴正方形c的面积为4.
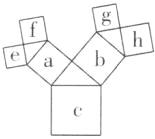
根据勾股定理可得x² + y² = 2² = 4,
∴正方形a的面积 + 正方形b的面积 = 4,
∴题图
(1)中所有正方形的面积和 = 4 + 4 = 8.同理可得正方形e的面积 + 正方形f的面积 = 正方形a的面积,正方形g的面积 + 正方形h的面积 = 正方形b的面积,
∴正方形e的面积 + 正方形f的面积 + 正方形g的面积 + 正方形h的面积 = 正方形a的面积 + 正方形b的面积 = 4,
∴题图
(2)中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 4 = 12,即1次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 4 = 12.同理可得2次操作后增加的8个小正方形的面积和也是4,
∴2次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 2×4 = 8 + 8 = 16,
∴根据规律可知10次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 10×4 = 8 + 40 = 48.
思路分析:根据勾股定理易得题图
(1)中所有正方形的面积和为8,经过1次操作后增加的4个小正方形的面积和为4,那么经过1次操作后图形中所有正方形的面积和 = 8 + 4,同理可得经过2次操作后增加的8个小正方形的面积和也为4,那么经过2次操作后图形中所有正方形的面积和 = 8 + 2×4,即可推断10次操作后图形中所有正方形的面积和 = 8 + 10×4 = 48.
48【解析】把题图
(2)中各个小正方形标上字母,如图.设正方形a的边长为x,正方形b的边长为y,
∴正方形a的面积为x²,正方形b的面积为y².由题意得正方形c的边长为2,并且其中一条边是直角三角形的斜边,
∴正方形c的面积为4.

根据勾股定理可得x² + y² = 2² = 4,
∴正方形a的面积 + 正方形b的面积 = 4,
∴题图
(1)中所有正方形的面积和 = 4 + 4 = 8.同理可得正方形e的面积 + 正方形f的面积 = 正方形a的面积,正方形g的面积 + 正方形h的面积 = 正方形b的面积,
∴正方形e的面积 + 正方形f的面积 + 正方形g的面积 + 正方形h的面积 = 正方形a的面积 + 正方形b的面积 = 4,
∴题图
(2)中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 4 = 12,即1次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 4 = 12.同理可得2次操作后增加的8个小正方形的面积和也是4,
∴2次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 2×4 = 8 + 8 = 16,
∴根据规律可知10次操作后图形中所有正方形的面积和 = 题图
(1)中所有正方形的面积和 + 10×4 = 8 + 40 = 48.
思路分析:根据勾股定理易得题图
(1)中所有正方形的面积和为8,经过1次操作后增加的4个小正方形的面积和为4,那么经过1次操作后图形中所有正方形的面积和 = 8 + 4,同理可得经过2次操作后增加的8个小正方形的面积和也为4,那么经过2次操作后图形中所有正方形的面积和 = 8 + 2×4,即可推断10次操作后图形中所有正方形的面积和 = 8 + 10×4 = 48.
5 [2023山东济宁中考]如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点A,B,C,D,E均在小正方形方格的顶点上,线段AB,CD交于点F,若∠CFB= α,则∠ABE等于( )
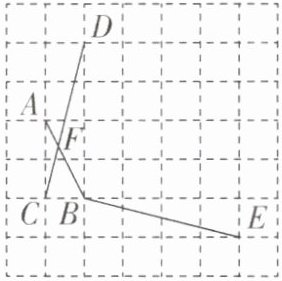
A.180° - α
B.180° - 2α
C.90° + α
D.90° + 2α

A.180° - α
B.180° - 2α
C.90° + α
D.90° + 2α
答案:
C【解析】如图,过B点作BG//CD,连接EG.
∵BG//CD,
∴∠ABG = ∠CFB = α.
∵BG² = 1² + 4² = 17,BE² = 1² + 4² = 17,EG² = 3² + 5² = 34,
∴BG² + BE² = EG²,
∴△BEG是直角三角形,且∠GBE = 90°,
∴∠ABE = ∠GBE + ∠ABG = 90° + α.故选C.

C【解析】如图,过B点作BG//CD,连接EG.
∵BG//CD,
∴∠ABG = ∠CFB = α.
∵BG² = 1² + 4² = 17,BE² = 1² + 4² = 17,EG² = 3² + 5² = 34,
∴BG² + BE² = EG²,
∴△BEG是直角三角形,且∠GBE = 90°,
∴∠ABE = ∠GBE + ∠ABG = 90° + α.故选C.

6 [2023广东中考]综合与实践
主题:制作无盖正方体形纸盒
素材:一张正方形纸板.
步骤1:如图(1),将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图(2),把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
(1)直接写出纸板上∠ABC与纸盒上$∠A_1B_1C_1$的大小关系;
(2)证明(1)中你发现的结论.
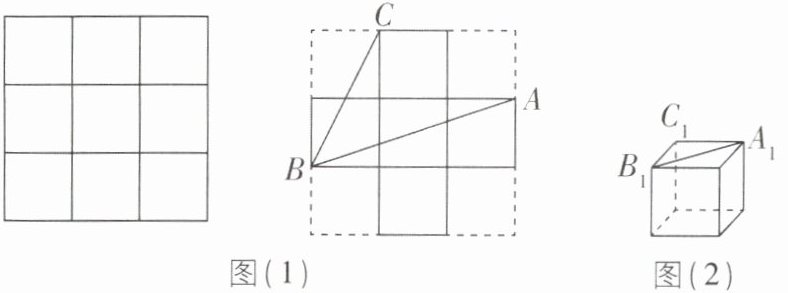
主题:制作无盖正方体形纸盒
素材:一张正方形纸板.
步骤1:如图(1),将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图(2),把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
(1)直接写出纸板上∠ABC与纸盒上$∠A_1B_1C_1$的大小关系;
(2)证明(1)中你发现的结论.

答案:
(1)【解】∠ABC = ∠A₁B₁C₁.
(2)【证明】如图,连接AC.设小正方形的边长为1,则AC = BC = $\sqrt{1² + 2²}$ = $\sqrt{5}$,AB = $\sqrt{1² + 3²}$ = $\sqrt{10}$.
∵AC² + BC² = 5 + 5 = 10 = AB²,
∴△ABC为等腰直角三角形,且∠ACB = 90°,
∴∠ABC = 45°.
∵A₁C₁ = B₁C₁,A₁C₁⊥B₁C₁,
∴△A₁B₁C₁为等腰直角三角形,且∠A₁C₁B₁ = 90°,
∴∠A₁B₁C₁ = 45°,
∴∠ABC = ∠A₁B₁C₁.

(1)【解】∠ABC = ∠A₁B₁C₁.
(2)【证明】如图,连接AC.设小正方形的边长为1,则AC = BC = $\sqrt{1² + 2²}$ = $\sqrt{5}$,AB = $\sqrt{1² + 3²}$ = $\sqrt{10}$.
∵AC² + BC² = 5 + 5 = 10 = AB²,
∴△ABC为等腰直角三角形,且∠ACB = 90°,
∴∠ABC = 45°.
∵A₁C₁ = B₁C₁,A₁C₁⊥B₁C₁,
∴△A₁B₁C₁为等腰直角三角形,且∠A₁C₁B₁ = 90°,
∴∠A₁B₁C₁ = 45°,
∴∠ABC = ∠A₁B₁C₁.

查看更多完整答案,请扫码查看


