《2025年初中必刷题八年级数学上册苏科版》

在平面直角坐标系中,点$A(1,5)$,$B(m-2,m+1)$,若直线$AB与y$轴垂直,则$m$的值为 (C)
A.0
B.3
C.4
D.7

答案： C 【解析】
∵点$A(1,5)$,$B(m-2,m+1)$,直线 AB 与 y 轴垂直,
∴$m+1=5$,解得$m=4$,故选 C.

坐标平面内有一点$A(x,y)$,且点$A到x$轴的距离为 3,到$y轴的距离恰为到x$轴距离的 2 倍. 若$xy＜0$,则点$A$的坐标为 (D)
A.$(6,-3)$
B.$(-6,3)$
C.$(3,-6)或(-3,6)$
D.$(6,-3)或(-6,3)$

答案： D 【解析】
∵$xy＜0$,
∴x,y 异号.
∵点 A 到 x 轴的距离为 3,到 y 轴的距离恰为到 x 轴距离的 2 倍,
∴点 A 的坐标为(6,-3)或(-6,3),故选 D.

3 [2024 四川眉山期中,中]若$m$是任意实数,则点$P(m-3,m+2)$一定不在 (D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： D 【解析】
∵$(m+2)-(m-3)=m+2-m+3=5＞0$,
∴点 P 的纵坐标一定大于横坐标.
∵第四象限的点的横坐标是正数,纵坐标是负数,
∴第四象限的点的纵坐标一定小于横坐标,
∴点 P 一定不在第四象限.故选 D.

4 [中]已知点$P(x,y)$在第二象限,且$y\leqslant 2x+6$,$x$,$y$均为整数,则符合要求的点$P$的个数是 (B)
A.3
B.6
C.10
D.无数

答案： B 【解析】
∵点$P(x,y)$位于第二象限,
∴$x＜0$,$y＞0$.又
∵$y\leq2x+6$,
∴$2x+6＞0$,即$x＞-3$,
∴$-3＜x＜0$,则$x=-1$或-2.当$x=-1$时,$0＜y\leq4$,则$y=1,2,3,4$;当$x=-2$时,$0＜y\leq2$,则$y=1$或 2.综上所述,点 P 的坐标为(-1,1),(-1,2),(-1,3),(-1,4),(-2,1),(-2,2),共 6 个.故选 B.

5 [中]已知点$P(2a-4,a+1)$,若点$P$在坐标轴上,则点$P$的坐标为(-6,0)或(0,3)。

答案： (-6,0)或(0,3) 【解析】分两种情况:当点 P 在 x 轴上时,$a+1=0$,
∴$a=-1$.当$a=-1$时,$2a-4=-6$,
∴点 P 的坐标为(-6,0);当点 P 在 y 轴上时,$2a-4=0$,
∴$a=2$.当$a=2$时,$a+1=3$,
∴点 P 的坐标为(0,3).故答案为(-6,0)或(0,3).

6 新考法 [2025 江苏常州期中,较难]如图,平面中两条直线$l_{1}和l_{2}相交于点O$,对于平面上任意一点$M$,若点$M到直线l_{1}$,$l_{2}的距离分别是p\ cm$,$q\ cm$,则称有序实数对$(p,q)是点M$的“距离坐标”. 特别地,当点在直线上时,定义点到直线的距离为 0. 下列说法：

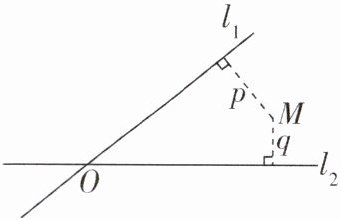
①“距离坐标”是$(0,0)的点只有点O$；
②“距离坐标”是$(0,1)$的点只有 1 个；
③“距离坐标”是$(2,2)$的点共有 4 个.
其中正确的有______(填序号)。①③

答案： ①③ 【解析】根据题意可知常数$p\geq0$,$q\geq0$,当$p=0$,$q=0$时,"距离坐标"是(0,0),则"距离坐标"为(0,0)的点有且仅有 1 个,为点 O,故①正确;当$p=0$,$q=1$时,$l_{1}$和到$l_{2}$的距离为 1 的两条直线共有 2 个交点,则"距离坐标"为(0,1)的点有 2 个,故②错误;当$p=2$,$q=2$时,与$l_{1}$距离是 2 的两条直线和与$l_{2}$距离是 2 的两条直线共有 4 个交点,则"距离坐标"为(2,2)的点共有 4 个,故③正确.故答案为①③.

(1)若点$P的坐标为(-1,5)$,则它的“3 级关联点”的坐标为(2,14)。
(2)若点$P$的“5 级关联点”的坐标为$(9,-3)$,求点$P$的坐标。(2,-1)
(3)若点$P(m-1,2m)$的“-3 级关联点”$P'$位于坐标轴上,求点$P'$的坐标。$(\frac{16}{5},0)$或(0,-16)

答案：
(1)(2,14)
(2)(2,-1)
(3)$(\frac{16}{5},0)$或(0,-16) 【解】
(1)$3×(-1)+5=2$,$-1+3×5=14$,
∴点 P 的"3 级关联点"的坐标为(2,14).故答案为(2,14).
(2)设点 P 的坐标为(n,b).由题意可知$\left\{\begin{array}{l} 5n+b=9,\\ n+5b=-3,\end{array}\right.$解得$\left\{\begin{array}{l} n=2,\\ b=-1,\end{array}\right.$
∴点 P 的坐标为(2,-1).
(3)由题意得点$P(m-1,2m)$的"-3 级关联点"为$P'(-3(m-1)+2m,m-1+(-3)×2m)$.①当$P'$位于 x 轴上时,$m-1+(-3)×2m=0$,解得$m=-\frac{1}{5}$,
∴$-3(m-1)+2m=\frac{16}{5}$,
∴$P'(\frac{16}{5},0)$.②当$P'$位于 y 轴上时,$-3(m-1)+2m=0$,解得$m=3$,
∴$m-1+(-3)×2m=-16$,
∴$P'(0,-16)$.综上所述,点$P'$的坐标为$(\frac{16}{5},0)$或(0,-16).

8 核心素养·应用意识 [难]先阅读下列文字,再回答相应问题：
在平面内有$P_{1}(x_{1},y_{1})$,$P_{2}(x_{2},y_{2})$两点,则两点间的距离可表示为$P_{1}P_{2}= \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$,$P_{1}P_{2}的中点M的坐标为(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2})$。
(1)已知$A(-2,1)$,$B(1,5)$,试求$A$,$B$两点间的距离。
(2)已知$A$,$B在平行于x$轴的直线上,$A$点的横坐标为-5,$B$点的横坐标为 3,试求$A$,$B$两点的距离。
(3)若$\triangle ABC各顶点的坐标为A(-2,0)$,$B(2,0)$,$C(0,1)$,试判断$\triangle ABC$的形状。
(4)已知点$A(3,-2)$,$B(0,1)$,$C(-3,4)$,试探究$A$,$B$,$C$三点的位置关系。

答案：
(1)5
(2)8
(3)等腰三角形
(4)A,B,C 三点在同一条直线上，且 B 为 AC 中点 【解】
(1)$AB=\sqrt{(1+2)^{2}+(5-1)^{2}}=\sqrt{9+16}=\sqrt{25}=5$.
(2)由题意可设$A(-5,y_{0})$,$B(3,y_{0})$,则$AB=\sqrt{(3+5)^{2}+(y_{0}-y_{0})^{2}}=\sqrt{64}=8$.
(3)$\triangle ABC$为等腰三角形.理由:$AB=\sqrt{(2+2)^{2}+(0-0)^{2}}=\sqrt{16}=4$,$AC=\sqrt{(0+2)^{2}+(1-0)^{2}}=\sqrt{5}$,$BC=\sqrt{(0-2)^{2}+(1-0)^{2}}=\sqrt{5}$,
∴$AC=BC\neq AB$,
∴$\triangle ABC$是等腰三角形.
(4)A,B,C 三点在同一条直线上,且 B 为 AC 中点.
∵$A(3,-2)$,$C(-3,4)$,
∴令 AC 的中点为 D 点,则$D(\frac{3+(-3)}{2},\frac{-2+4}{2})$,即$D(0,1)$.又
∵$B(0,1)$,
∴点 D 与点 B 重合,
∴A,B,C 三点在同一条直线上,且 B 为 AC 中点.