第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
9 [2024湖南中考]如图,在锐角三角形$ABC$中,$AD是边 BC$上的高,在$BA$,$BC上分别截取线段BE$,$BF$,使$BE= BF$;分别以点$E$,$F$为圆心,大于$\frac{1}{2}EF$的长为半径画弧,在$\angle ABC$内,两弧交于点$P$,作射线$BP$,交$AD于点M$,过点$M作MN\perp AB于点N$。若$MN= 2$,$AD= 4MD$,则$AM= $
BC$上的高,在$BA$,$BC上分别截取线段BE$,$BF$,使$BE= BF$;分别以点$E$,$F$为圆心,大于$\frac{1}{2}EF$的长为半径画弧,在$\angle ABC$内,两弧交于点$P$,作射线$BP$,交$AD于点M$,过点$M作MN\perp AB于点N$。若$MN= 2$,$AD= 4MD$,则$AM= $
 BC$上的高,在$BA$,$BC上分别截取线段BE$,$BF$,使$BE= BF$;分别以点$E$,$F$为圆心,大于$\frac{1}{2}EF$的长为半径画弧,在$\angle ABC$内,两弧交于点$P$,作射线$BP$,交$AD于点M$,过点$M作MN\perp AB于点N$。若$MN= 2$,$AD= 4MD$,则$AM= $
BC$上的高,在$BA$,$BC上分别截取线段BE$,$BF$,使$BE= BF$;分别以点$E$,$F$为圆心,大于$\frac{1}{2}EF$的长为半径画弧,在$\angle ABC$内,两弧交于点$P$,作射线$BP$,交$AD于点M$,过点$M作MN\perp AB于点N$。若$MN= 2$,$AD= 4MD$,则$AM= $6
。
答案:
6 【解析】由作图可知 BP 平分∠ABC.
∵ AD 是边 BC 上的高,MN⊥AB,MN=2,
∴ MD=MN=2.
∵ AD=4MD,
∴ AD=8,
∴ AM=AD - MD=6,故答案为 6.
∵ AD 是边 BC 上的高,MN⊥AB,MN=2,
∴ MD=MN=2.
∵ AD=4MD,
∴ AD=8,
∴ AM=AD - MD=6,故答案为 6.
10 [2024四川南充中考]如图,在$\triangle ABC$中,点$D为BC$边的中点,过点$B作BE// AC交AD的延长线于点E$。
(1)求证:$\triangle BDE\cong\triangle CDA$。
(2)若$AD\perp BC$,求证:$BA= BE$。

(1)求证:$\triangle BDE\cong\triangle CDA$。
(2)若$AD\perp BC$,求证:$BA= BE$。

答案:
【证明】
(1)
∵ D 为 BC 的中点,
∴ BD=CD.
∵ BE//AC,
∴ ∠E=∠DAC,∠DBE=∠C.在△BDE 和△CDA 中,{∠E=∠DAC,∠DBE=∠C,BD=CD},
∴ △BDE≌△CDA(AAS).
(2)
∵ △BDE≌△CDA,
∴ ED=AD.
∵ AD⊥BC,
∴ BD 垂直平分 AE,
∴ BA=BE.
(1)
∵ D 为 BC 的中点,
∴ BD=CD.
∵ BE//AC,
∴ ∠E=∠DAC,∠DBE=∠C.在△BDE 和△CDA 中,{∠E=∠DAC,∠DBE=∠C,BD=CD},
∴ △BDE≌△CDA(AAS).
(2)
∵ △BDE≌△CDA,
∴ ED=AD.
∵ AD⊥BC,
∴ BD 垂直平分 AE,
∴ BA=BE.
11 [2024甘肃兰州中考]如图,在$\triangle ABC$中,$AB= AC$,$\angle BAC= 130^{\circ}$,$DA\perp AC$,则$\angle ADB= $(

A.$100^{\circ}$
B.$115^{\circ}$
C.$130^{\circ}$
D.$145^{\circ}$
B
)
A.$100^{\circ}$
B.$115^{\circ}$
C.$130^{\circ}$
D.$145^{\circ}$
答案:
B 【解析】
∵ AB=AC,∠BAC=130°,
∴ ∠C=$\frac{180° - ∠BAC}{2}$=25°.
∵ DA⊥AC,
∴ ∠CAD=90°,
∴ ∠ADB=∠C+∠CAD=115°.故选 B.
∵ AB=AC,∠BAC=130°,
∴ ∠C=$\frac{180° - ∠BAC}{2}$=25°.
∵ DA⊥AC,
∴ ∠CAD=90°,
∴ ∠ADB=∠C+∠CAD=115°.故选 B.
如图,直线$l// m$,等边三角形$ABC的两个顶点B$,$C分别落在直线l$,$m$上,若$\angle ABE= 21^{\circ}$,则$\angle ACD$的度数是(
A.$45^{\circ}$
B.$39^{\circ}$
C.$29^{\circ}$
D.$21^{\circ}$
B
)A.$45^{\circ}$
B.$39^{\circ}$
C.$29^{\circ}$
D.$21^{\circ}$
答案:
B 【解析】
∵ l//m,
∴ ∠EBC+∠DCB=180°,即∠EBA+∠ABC+∠ACB+∠ACD=180°.
∵ △ABC 是等边三角形,
∴ ∠ABC=∠ACB=60°.又
∵ ∠ABE=21°,
∴ 21°+60°+60°+∠ACD=180°,
∴ ∠ACD=39°.故选 B.
∵ l//m,
∴ ∠EBC+∠DCB=180°,即∠EBA+∠ABC+∠ACB+∠ACD=180°.
∵ △ABC 是等边三角形,
∴ ∠ABC=∠ACB=60°.又
∵ ∠ABE=21°,
∴ 21°+60°+60°+∠ACD=180°,
∴ ∠ACD=39°.故选 B.
13 [2024四川内江中考]如图,在$\triangle ABC$中,$\angle DCE= 40^{\circ}$,$AE= AC$,$BC= BD$,则$\angle ACB$的度数为____

100°
。
答案:
100° 【解析】
∵ ∠DCE=40°,
∴ ∠CDE+∠CED=180° - ∠DCE=140°.
∵ AE=AC,BC=BD,
∴ ∠ACE=∠CED,∠BCD=∠CDE,
∴ ∠ACE+∠BCD=∠CED+∠CDE=140°,
∴ ∠ACB=∠ACE+∠BCE=∠ACE+∠BCD - ∠DCE=140° - 40°=100°.故答案为 100°.
∵ ∠DCE=40°,
∴ ∠CDE+∠CED=180° - ∠DCE=140°.
∵ AE=AC,BC=BD,
∴ ∠ACE=∠CED,∠BCD=∠CDE,
∴ ∠ACE+∠BCD=∠CED+∠CDE=140°,
∴ ∠ACB=∠ACE+∠BCE=∠ACE+∠BCD - ∠DCE=140° - 40°=100°.故答案为 100°.
14 [2024陕西中考]如图,已知直线$l和l外一点A$,请用尺规作图法,求作一个等腰直角$\triangle ABC$,使得顶点$B和顶点C都在直线l$上。(作出符合题意的一个等腰直角三角形即可,保留作图痕迹,不写作法)


答案:
【解】等腰直角△ABC 如图所示.(答案不唯一)

【解】等腰直角△ABC 如图所示.(答案不唯一)

15 [2024湖南长沙中考]如图,点$C在线段AD$上,$AB= AD$,$\angle B= \angle D$,$BC= DE$。
(1)求证:$\triangle ABC\cong\triangle ADE$;
(2)若$\angle BAC= 60^{\circ}$,求$\angle ACE$的度数。

(1)求证:$\triangle ABC\cong\triangle ADE$;
(2)若$\angle BAC= 60^{\circ}$,求$\angle ACE$的度数。

答案:
(1)【证明】在△ABC 和△ADE 中,{BC=DE,∠B=∠D,AB=AD},
∴ △ABC≌△ADE(SAS).
(2)【解】
∵ △ABC≌△ADE,
∴ AC=AE,∠CAE=∠BAC=60°,
∴ △ACE 是等边三角形,
∴ ∠ACE=60°.
(1)【证明】在△ABC 和△ADE 中,{BC=DE,∠B=∠D,AB=AD},
∴ △ABC≌△ADE(SAS).
(2)【解】
∵ △ABC≌△ADE,
∴ AC=AE,∠CAE=∠BAC=60°,
∴ △ACE 是等边三角形,
∴ ∠ACE=60°.
16 [2024广东广州中考改编]如图,在$\triangle ABC$中,$\angle A= 90^{\circ}$,$AB= AC= 6$,$D为边BC$的中点,点$E$,$F分别在边AB$,$AC$上,$AE= CF$,则四边形$AEDF$的面积为____。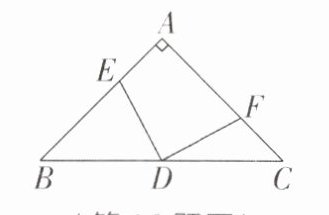

答案:
1. 首先,连接$AD$:
因为$\angle A = 90^{\circ}$,$AB = AC = 6$,$D$为$BC$中点,根据等腰直角三角形的性质:
$AD = BD = CD$,$\angle BAD=\angle CAD = 45^{\circ}=\angle C$,$AD\perp BC$。
2. 然后,证明$\triangle ADE\cong\triangle CDF$:
在$\triangle ADE$和$\triangle CDF$中,$\left\{\begin{array}{l}AE = CF\\\angle EAD=\angle C\\AD = CD\end{array}\right.$。
根据$SAS$(边角边)判定定理,可得$\triangle ADE\cong\triangle CDF$。
3. 接着,求四边形$AEDF$的面积:
因为$S_{四边形AEDF}=S_{\triangle ADE}+S_{\triangle ADF}$,又$S_{\triangle ADE}=S_{\triangle CDF}$。
所以$S_{四边形AEDF}=S_{\triangle CDF}+S_{\triangle ADF}$。
而$S_{\triangle CDF}+S_{\triangle ADF}=S_{\triangle ADC}$。
再根据三角形面积公式$S=\frac{1}{2}ah$(对于$\triangle ABC$,$a = AB$,$h = AC$),$S_{\triangle ABC}=\frac{1}{2}× AB× AC$,把$AB = AC = 6$代入,得$S_{\triangle ABC}=\frac{1}{2}×6×6 = 18$。
因为$D$是$BC$中点,所以$S_{\triangle ADC}=\frac{1}{2}S_{\triangle ABC}$(等底同高的三角形面积关系:中线将三角形分成面积相等的两部分)。
所以$S_{四边形AEDF}=S_{\triangle ADC}=\frac{1}{2}×\frac{1}{2}× AB× AC=\frac{1}{2}×18 = 9$。
故四边形$AEDF$的面积为$9$。
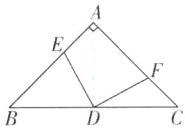
1. 首先,连接$AD$:
因为$\angle A = 90^{\circ}$,$AB = AC = 6$,$D$为$BC$中点,根据等腰直角三角形的性质:
$AD = BD = CD$,$\angle BAD=\angle CAD = 45^{\circ}=\angle C$,$AD\perp BC$。
2. 然后,证明$\triangle ADE\cong\triangle CDF$:
在$\triangle ADE$和$\triangle CDF$中,$\left\{\begin{array}{l}AE = CF\\\angle EAD=\angle C\\AD = CD\end{array}\right.$。
根据$SAS$(边角边)判定定理,可得$\triangle ADE\cong\triangle CDF$。
3. 接着,求四边形$AEDF$的面积:
因为$S_{四边形AEDF}=S_{\triangle ADE}+S_{\triangle ADF}$,又$S_{\triangle ADE}=S_{\triangle CDF}$。
所以$S_{四边形AEDF}=S_{\triangle CDF}+S_{\triangle ADF}$。
而$S_{\triangle CDF}+S_{\triangle ADF}=S_{\triangle ADC}$。
再根据三角形面积公式$S=\frac{1}{2}ah$(对于$\triangle ABC$,$a = AB$,$h = AC$),$S_{\triangle ABC}=\frac{1}{2}× AB× AC$,把$AB = AC = 6$代入,得$S_{\triangle ABC}=\frac{1}{2}×6×6 = 18$。
因为$D$是$BC$中点,所以$S_{\triangle ADC}=\frac{1}{2}S_{\triangle ABC}$(等底同高的三角形面积关系:中线将三角形分成面积相等的两部分)。
所以$S_{四边形AEDF}=S_{\triangle ADC}=\frac{1}{2}×\frac{1}{2}× AB× AC=\frac{1}{2}×18 = 9$。
故四边形$AEDF$的面积为$9$。

17 [2024新疆中考]如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,$\angle A= 30^{\circ}$,$AB= 8$。若点$D在直线AB$上(不与点$A$,$B$重合),且$\angle BCD= 30^{\circ}$,则$AD$的长为____。


答案:
6 或 12 【解析】
∵ ∠ACB=90°,∠A=30°,AB=8,
∴ ∠B=60°,BC=$\frac{1}{2}$AB=4.①当点 D 在线段 AB 上时,如图
(1).
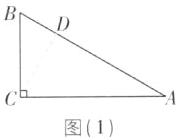
∵ ∠BCD=30°,∠B=60°,
∴ ∠BDC=90°,
∴ BD=$\frac{1}{2}$BC=2,
∴ AD=AB - BD=6.②当点 D 在线段 AB 的延长线上时,如图
(2).
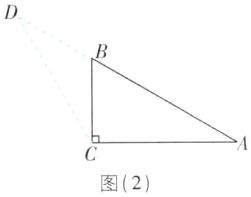
∵ ∠BCD=30°,∠ABC=60°,
∴ ∠D=∠ABC - ∠BCD=30°=∠BCD,
∴ BC=BD=4,
∴ AD=AB+BD=12.③当点 D 在线段 BA 的延长线上时,如图
(3).
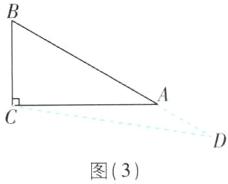
此时∠BCD>∠ACB,即∠BCD>90°,故不符合题意,舍去.综上,AD 的长为 6 或 12.
6 或 12 【解析】
∵ ∠ACB=90°,∠A=30°,AB=8,
∴ ∠B=60°,BC=$\frac{1}{2}$AB=4.①当点 D 在线段 AB 上时,如图
(1).

∵ ∠BCD=30°,∠B=60°,
∴ ∠BDC=90°,
∴ BD=$\frac{1}{2}$BC=2,
∴ AD=AB - BD=6.②当点 D 在线段 AB 的延长线上时,如图
(2).

∵ ∠BCD=30°,∠ABC=60°,
∴ ∠D=∠ABC - ∠BCD=30°=∠BCD,
∴ BC=BD=4,
∴ AD=AB+BD=12.③当点 D 在线段 BA 的延长线上时,如图
(3).

此时∠BCD>∠ACB,即∠BCD>90°,故不符合题意,舍去.综上,AD 的长为 6 或 12.
查看更多完整答案,请扫码查看


