第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2025 江苏南京期中,中]如果一个三角形一条边上的中点到其他两边距离相等,那么这个三角形一定是 ( )
A.等边三角形
B.等腰三角形
C.直角三角形
D.钝角三角形
A.等边三角形
B.等腰三角形
C.直角三角形
D.钝角三角形
答案:
B [解析]如图,△ABC中,D是BC边上的中点,DE⊥AB,DF⊥AC,E,F为垂足,且DE=DF,连接AD.
∵D是BC边上的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,E,F为垂足,且DE=DF,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.故选B.

B [解析]如图,△ABC中,D是BC边上的中点,DE⊥AB,DF⊥AC,E,F为垂足,且DE=DF,连接AD.
∵D是BC边上的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,E,F为垂足,且DE=DF,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.故选B.

2 [较难]如图所示,在$\triangle ABC$中,$AB = 8$,点$M是BC$的中点,$AD是∠BAC$的平分线,作$MF// AD交AC于F$. 已知$CF = 10$,则$AC$的长为( )
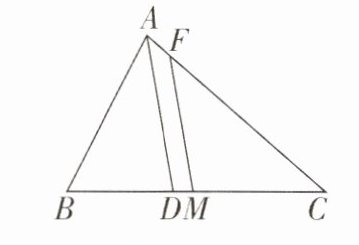
A.12
B.11
C.10
D.9

A.12
B.11
C.10
D.9
答案:
A
[解析]如图,延长FM到N,使MN=MF,连接BN,延长MF交BA的延长线于E.
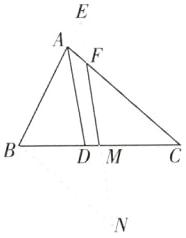
∵M是BC中点,
∴BM=CM.在△BMN和△CMF中,$\begin{cases} BM = CM \\ ∠BMN = ∠CMF \\ MN = MF \end{cases}$,
∴△BMN≌△CMF(SAS),
∴BN=CF,∠N=∠MFC;又
∵∠BAD=∠CAD,MF//AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC.
∵AB=8,CF=10,
∴AC=2FC−AB=20−8=12.故选A.
A
[解析]如图,延长FM到N,使MN=MF,连接BN,延长MF交BA的延长线于E.

∵M是BC中点,
∴BM=CM.在△BMN和△CMF中,$\begin{cases} BM = CM \\ ∠BMN = ∠CMF \\ MN = MF \end{cases}$,
∴△BMN≌△CMF(SAS),
∴BN=CF,∠N=∠MFC;又
∵∠BAD=∠CAD,MF//AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC.
∵AB=8,CF=10,
∴AC=2FC−AB=20−8=12.故选A.
3 [2024 江苏无锡锡山区期末,较难]如图,$\triangle ABC$中,$∠CAB = ∠CBA = 48^{\circ}$,点$O为\triangle ABC$内一点,$∠OAB = 12^{\circ}$,$∠OBC = 18^{\circ}$,则$∠ACO + ∠AOB = $ ( )
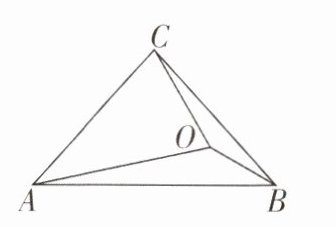
A.$190^{\circ}$
B.$195^{\circ}$
C.$200^{\circ}$
D.$210^{\circ}$

A.$190^{\circ}$
B.$195^{\circ}$
C.$200^{\circ}$
D.$210^{\circ}$
答案:
D [解析]如图,过点C作CD⊥AB,垂足为D,延长BO交CD于点P,连接AP.
∵∠OBC=18°,∠CBA=48°,
∴∠ABP=∠CBA−∠OBC=30°.
∵∠CAB=∠CBA=48°,
∴CA=CB.
∵CD⊥AB,
∴CD是AB的垂直平分线,
∴PA=PB,
∴∠PAB=∠PBA=30°,
∴∠CAP=∠CAB−∠PAB=18°.
∵∠AOP是△AOB的一个外角,
∴∠AOP=∠OAB+∠OBA=42°.
∵∠CDA=90°,
∴∠ACD=90°−∠CAD=42°,
∴∠AOP=∠ACD.
∵∠PAB=30°,∠OAB=12°,
∴∠PAO=∠PAB−∠OAB=18°,
∴∠CAP=∠OAP.
∵AP=AP,
∴△ACP≌△AOP(AAS),
∴AC=AO.
∵∠CAO=∠CAP+∠OAP=36°,
∴∠ACO=∠AOC=72°.
∵∠AOB=180°−∠OAB−∠OBA=138°,
∴∠ACO+∠AOB=210°,故选D.

D [解析]如图,过点C作CD⊥AB,垂足为D,延长BO交CD于点P,连接AP.
∵∠OBC=18°,∠CBA=48°,
∴∠ABP=∠CBA−∠OBC=30°.
∵∠CAB=∠CBA=48°,
∴CA=CB.
∵CD⊥AB,
∴CD是AB的垂直平分线,
∴PA=PB,
∴∠PAB=∠PBA=30°,
∴∠CAP=∠CAB−∠PAB=18°.
∵∠AOP是△AOB的一个外角,
∴∠AOP=∠OAB+∠OBA=42°.
∵∠CDA=90°,
∴∠ACD=90°−∠CAD=42°,
∴∠AOP=∠ACD.
∵∠PAB=30°,∠OAB=12°,
∴∠PAO=∠PAB−∠OAB=18°,
∴∠CAP=∠OAP.
∵AP=AP,
∴△ACP≌△AOP(AAS),
∴AC=AO.
∵∠CAO=∠CAP+∠OAP=36°,
∴∠ACO=∠AOC=72°.
∵∠AOB=180°−∠OAB−∠OBA=138°,
∴∠ACO+∠AOB=210°,故选D.

4 [2025 陕西西安校级期末,中]如图,$\triangle ABC$中,$AC = DC = 3$,$BD垂直∠BAC的平分线于D$,$E为AC$的中点,则图中两个阴影三角形($\triangle OBD与\triangle OAE$)的面积之差的最大值为______.
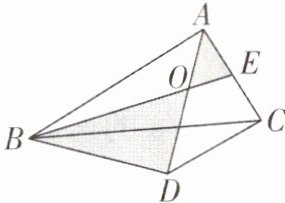

答案:
$\frac{9}{2}$ [解析]如图,延长BD,AC交于点H;
∵AD⊥BH,
∴∠ADB=∠ADH=90°,
∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵∠BAD=∠HAD,
∴∠ABD=∠H,
∴AB=AH.
∵AD⊥BH,
∴BD=DH.
∵DC=CA,
∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,
∴∠CDH=∠H,
∴CD=CH=AC.
∵AE=EC,
$∴S_{△ABE}=\frac{1}{4}S_{△ABH},S_{△CDH}=\frac{1}{4}S_{△ABH}$
$∴S_{△ABE}=S_{△CDH}.$
$∵S_{△OBD}−S_{△AOE}=S_{△ADB}−S_{△ABE}=S_{△ADH}−S_{△CDH}=S_{△ACD}.$
∵AC=CD=3,
∴当DC⊥AC时,△ACD的面积最大,最大面积为$\frac{1}{2}$×3×3 = $\frac{9}{2}$.故答案为$\frac{9}{2}$.

$\frac{9}{2}$ [解析]如图,延长BD,AC交于点H;
∵AD⊥BH,
∴∠ADB=∠ADH=90°,
∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵∠BAD=∠HAD,
∴∠ABD=∠H,
∴AB=AH.
∵AD⊥BH,
∴BD=DH.
∵DC=CA,
∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,
∴∠CDH=∠H,
∴CD=CH=AC.
∵AE=EC,
$∴S_{△ABE}=\frac{1}{4}S_{△ABH},S_{△CDH}=\frac{1}{4}S_{△ABH}$
$∴S_{△ABE}=S_{△CDH}.$
$∵S_{△OBD}−S_{△AOE}=S_{△ADB}−S_{△ABE}=S_{△ADH}−S_{△CDH}=S_{△ACD}.$
∵AC=CD=3,
∴当DC⊥AC时,△ACD的面积最大,最大面积为$\frac{1}{2}$×3×3 = $\frac{9}{2}$.故答案为$\frac{9}{2}$.

5 [2025 浙江宁波期末,中]如图(1),$P为∠AOB的平分线OC$上一点,过点$P作PD// OB交OA于点D$,易得$\triangle POD$为等腰三角形.
(1)【基本运用】如图(2),把长方形纸片$ABCD沿对角线AC$折叠,使点$B落在点B'$处,重合部分$\triangle ACE$是等腰三角形吗?为什么?
(2)【类比探究】如图(3),$\triangle ABC$中,内角$∠ABC与外角∠ACG的平分线交于点O$,过点$O作OD// BC分别交AB$,$AC于点D$,$E$,试探究线段$BD$,$DE$,$CE$之间的数量关系并说明理由.
(3)【拓展提升】如图(4),四边形$ABCD$中,$AD// BC$,$E为CD$边的中点,$AE平分∠BAD$,连接$BE$,求证:$AE⊥BE$.
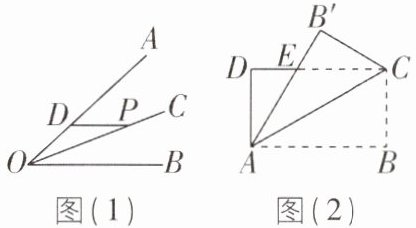
(1)【基本运用】如图(2),把长方形纸片$ABCD沿对角线AC$折叠,使点$B落在点B'$处,重合部分$\triangle ACE$是等腰三角形吗?为什么?
(2)【类比探究】如图(3),$\triangle ABC$中,内角$∠ABC与外角∠ACG的平分线交于点O$,过点$O作OD// BC分别交AB$,$AC于点D$,$E$,试探究线段$BD$,$DE$,$CE$之间的数量关系并说明理由.
(3)【拓展提升】如图(4),四边形$ABCD$中,$AD// BC$,$E为CD$边的中点,$AE平分∠BAD$,连接$BE$,求证:$AE⊥BE$.


答案:
(1)[解]△ACE是等腰三角形.理由:在长方形ABCD中,
∵DC//AB,
∴∠ACD=∠BAC.由折叠性质可得∠BAC=∠B'AC,
∴∠ACD=∠B'AC,
∴AE=CE,
∴△ACE是等腰三角形.
(2)[解]BD=DE+CE.理由如下:同理
(1)可证△BDO为等腰三角形,BD=OD.
∵CO平分∠ACG,DO//BC,
∴∠ECO=∠OCG=∠EOC,
∴CE=OE,
∴△COE为等腰三角形.
∵BD=DO=DE+EO,
∴BD=DE+CE.
(3)[证明]如图,延长AE交BC的延长线于F.
∵AD//BC,
∴∠F=∠DAE,∠D=∠ECF.
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∴∠BAF=∠F,
∴BA=BF.
∵E是CD的中点,
∴DE=CE.在△ADE和△FCE中,$\begin{cases} ∠DAE = ∠CFE \\ ∠ADE = ∠FCE \\ DE = CE \end{cases}$,
∴△ADE≌△FCE(AAS),
∴AE=EF,
∴点E是AF的中点,
∴BE⊥AE.

(1)[解]△ACE是等腰三角形.理由:在长方形ABCD中,
∵DC//AB,
∴∠ACD=∠BAC.由折叠性质可得∠BAC=∠B'AC,
∴∠ACD=∠B'AC,
∴AE=CE,
∴△ACE是等腰三角形.
(2)[解]BD=DE+CE.理由如下:同理
(1)可证△BDO为等腰三角形,BD=OD.
∵CO平分∠ACG,DO//BC,
∴∠ECO=∠OCG=∠EOC,
∴CE=OE,
∴△COE为等腰三角形.
∵BD=DO=DE+EO,
∴BD=DE+CE.
(3)[证明]如图,延长AE交BC的延长线于F.
∵AD//BC,
∴∠F=∠DAE,∠D=∠ECF.
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∴∠BAF=∠F,
∴BA=BF.
∵E是CD的中点,
∴DE=CE.在△ADE和△FCE中,$\begin{cases} ∠DAE = ∠CFE \\ ∠ADE = ∠FCE \\ DE = CE \end{cases}$,
∴△ADE≌△FCE(AAS),
∴AE=EF,
∴点E是AF的中点,
∴BE⊥AE.

6 核心素养 几何直观 [较难]在$\triangle ABC$中,$AB = AC$,$D是BC$的中点,$E$,$F分别是边AD$,$AC$上的点.
(1)如图(1),连接$BE$,$EF$,若$∠ABE = ∠EFC$,求证:$BE = EF$;
(2)如图(2),若$B$,$E$,$F$在一条直线上,且$∠ABE = ∠BAC = 45^{\circ}$,探究$BD与AE$之间的数量关系,并说明理由.
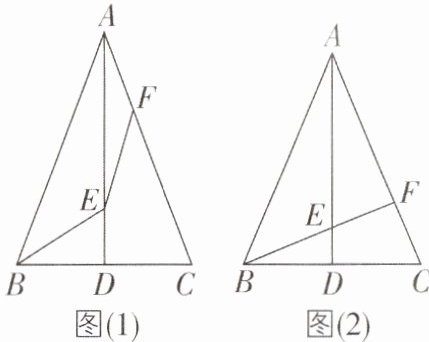
(1)如图(1),连接$BE$,$EF$,若$∠ABE = ∠EFC$,求证:$BE = EF$;
(2)如图(2),若$B$,$E$,$F$在一条直线上,且$∠ABE = ∠BAC = 45^{\circ}$,探究$BD与AE$之间的数量关系,并说明理由.

答案:
(1)[证明]连接CE,如图
(1).
∵AB=AC,D是BC边的中点,
∴AD⊥BC,∠ABC=∠ACB,
∴AD垂直平分BC,
∴BE=CE,
∴∠EBC=∠ECB,
∴∠ABC−∠EBC=∠ACB−∠ECB,即∠ABE=∠ACE.
∵∠ABE=∠EFC,
∴∠ACE=∠EFC,
∴EF=CE,
∴BE=EF.

(2)[解]AE=2BD.理由如下:连接CE,如图
(2).由
(1)得,∠ABE=∠ACE.
∵∠ABE=∠BAC=45°,
∴∠ACE=45°,∠AFB=∠CFE=90°,
∴△ABF和△CEF都是等腰直角三角形,
∴AF=BF,CF=EF.在△CBF和△EAF中,$\begin{cases} BF = AF \\ ∠BFC = ∠AFE \\ CF = EF \end{cases}$,
∴△CBF≌△EAF(SAS),
∴BC=AE.
∵BC=2BD,
∴AE=2BD.

模型中已知角平分线和平行线,那么等腰三角形必出现.
图示:

∠1=∠2,AB//CD,
∴∠2=∠3=∠1,
∴AC=AB,
∴△ABC为等腰三角形.
归纳总结:判定等边三角形的方法:
(1)由定义判定:三条边都相等的三角形是等边三角形
(2)判定定理1:三个角都相等的三角形是等边三角形
(3)判定定理2:有一个角是60°的等腰三角形是等边三角形
(1)[证明]连接CE,如图
(1).
∵AB=AC,D是BC边的中点,
∴AD⊥BC,∠ABC=∠ACB,
∴AD垂直平分BC,
∴BE=CE,
∴∠EBC=∠ECB,
∴∠ABC−∠EBC=∠ACB−∠ECB,即∠ABE=∠ACE.
∵∠ABE=∠EFC,
∴∠ACE=∠EFC,
∴EF=CE,
∴BE=EF.

(2)[解]AE=2BD.理由如下:连接CE,如图
(2).由
(1)得,∠ABE=∠ACE.
∵∠ABE=∠BAC=45°,
∴∠ACE=45°,∠AFB=∠CFE=90°,
∴△ABF和△CEF都是等腰直角三角形,
∴AF=BF,CF=EF.在△CBF和△EAF中,$\begin{cases} BF = AF \\ ∠BFC = ∠AFE \\ CF = EF \end{cases}$,
∴△CBF≌△EAF(SAS),
∴BC=AE.
∵BC=2BD,
∴AE=2BD.

模型中已知角平分线和平行线,那么等腰三角形必出现.
图示:

∠1=∠2,AB//CD,
∴∠2=∠3=∠1,
∴AC=AB,
∴△ABC为等腰三角形.
归纳总结:判定等边三角形的方法:
(1)由定义判定:三条边都相等的三角形是等边三角形
(2)判定定理1:三个角都相等的三角形是等边三角形
(3)判定定理2:有一个角是60°的等腰三角形是等边三角形
查看更多完整答案,请扫码查看


