第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
1 [2025山东淄博一模]如图,$\triangle ACE\cong\triangle DBF$,$\angle A= 67^{\circ}$,$\angle F= 48^{\circ}$,则$\angle ACE$的度数为(
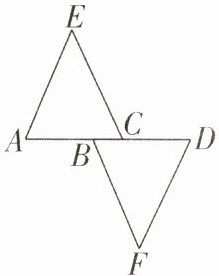
A.$76^{\circ}$
B.$67^{\circ}$
C.$65^{\circ}$
D.$56^{\circ}$
C
)
A.$76^{\circ}$
B.$67^{\circ}$
C.$65^{\circ}$
D.$56^{\circ}$
答案:
C 【解析】
∵ △ACE≌△DBF,
∴ ∠F=∠E=48°,
∴ ∠ACE=180° - ∠A - ∠E=180° - 67° - 48°=65°,故选 C.
∵ △ACE≌△DBF,
∴ ∠F=∠E=48°,
∴ ∠ACE=180° - ∠A - ∠E=180° - 67° - 48°=65°,故选 C.
2 [2024吉林长春绿园区质检]小丽同学要找到到三角形三个顶点距离相等的点,根据下列各图中圆规作图的痕迹,可用直尺成功找到此点的是(

B
)
答案:
B 【解析】到三角形三个顶点距离相等的点是三角形的三边垂直平分线的交点,选项 B 满足条件.故选 B.
3 [2025河北邢台期中]如图,在$\triangle ABC$中,$\triangle ADB\cong\triangle CDE$,则下列结论不一定正确的是( )

A.$BD= DE$
B.$AB\perp CE$
C.$AB= CE$
D.$AE= DE$

A.$BD= DE$
B.$AB\perp CE$
C.$AB= CE$
D.$AE= DE$
答案:
D 【解析】如图,延长 CE 交 AB 于 F.
∵ △ADB≌△CDE,
∴ BD=DE,AB=CE,∠BAD=∠ECD,∠ADB=∠CDE,故选项 A、C 正确,不符合题意.
∵ ∠ADB+∠CDE=180°,
∴ ∠ADB=∠CDE=90°,
∴ ∠BAD+∠B=90°,
∴ ∠ECD+∠B=90°,
∴ ∠CFB=180° - (∠FCB+∠B)=90°,即 AB⊥CE,故选项 B 正确,不符合题意.AE 和 DE 不一定相等,故选项 D 错误,符合题意.故选 D.

D 【解析】如图,延长 CE 交 AB 于 F.
∵ △ADB≌△CDE,
∴ BD=DE,AB=CE,∠BAD=∠ECD,∠ADB=∠CDE,故选项 A、C 正确,不符合题意.
∵ ∠ADB+∠CDE=180°,
∴ ∠ADB=∠CDE=90°,
∴ ∠BAD+∠B=90°,
∴ ∠ECD+∠B=90°,
∴ ∠CFB=180° - (∠FCB+∠B)=90°,即 AB⊥CE,故选项 B 正确,不符合题意.AE 和 DE 不一定相等,故选项 D 错误,符合题意.故选 D.

如图,$\triangle ABC$中,$AB= AC$,把$\triangle ABC沿线段DE$折叠,使点$B落在点F$处,若$AC// DE$,$\angle A= \alpha$,则$\angle CEF$的度数为(
A.$\alpha$
B.$90^{\circ}-\alpha$
C.$90^{\circ}+\alpha$
D.$180^{\circ}-2\alpha$
A
)A.$\alpha$
B.$90^{\circ}-\alpha$
C.$90^{\circ}+\alpha$
D.$180^{\circ}-2\alpha$
答案:
A 【解析】
∵ ∠A=α,AB=AC,
∴ ∠C=$\frac{180° - α}{2}$=90° - $\frac{1}{2}$α.
∵ AC//DE,
∴ ∠DEB=∠C=90° - $\frac{1}{2}$α.
∵ 把△ABC 沿线段 DE 折叠,使点 B 落在点 F 处,
∴ ∠DEB=∠DEF=90° - $\frac{1}{2}$α,
∴ ∠CEF=180° - ∠DEB - ∠DEF=180° - 2(90° - $\frac{1}{2}$α)=α.故选 A.
∵ ∠A=α,AB=AC,
∴ ∠C=$\frac{180° - α}{2}$=90° - $\frac{1}{2}$α.
∵ AC//DE,
∴ ∠DEB=∠C=90° - $\frac{1}{2}$α.
∵ 把△ABC 沿线段 DE 折叠,使点 B 落在点 F 处,
∴ ∠DEB=∠DEF=90° - $\frac{1}{2}$α,
∴ ∠CEF=180° - ∠DEB - ∠DEF=180° - 2(90° - $\frac{1}{2}$α)=α.故选 A.
5 [2024江苏无锡江阴调研]如图,在五边形$ABCDE$中,$\angle B= \angle E= 90^{\circ}$,在$BC$,$DE上分别找一点M$,$N$,使得$\angle AMN+\angle ANM= 88^{\circ}$,当$\triangle AMN$的周长最小时,$\angle BAE$的度数为( )

A.$136^{\circ}$
B.$96^{\circ}$
C.$90^{\circ}$
D.$84^{\circ}$

A.$136^{\circ}$
B.$96^{\circ}$
C.$90^{\circ}$
D.$84^{\circ}$
答案:
A 【解析】如图,作点 A 关于 BC 的对称点 P,关于 DE 的对称点 Q,连接 PQ 与 BC 相交于点 M,与 DE 相交于点 N,则 AM=PM,AN=QN,
∴ ∠P=∠PAM,∠Q=∠QAN,
∴ △AMN 周长为 AM+MN+AN=PM+MN+QN≥PQ,
∴ 当 P,M,N,Q 在一条直线上时,PQ 的长度即为△AMN 周长的最小值.
∵ ∠AMN=∠P+∠PAM=2∠P,∠ANM=∠Q+∠QAN=2∠Q,
∴ ∠AMN+∠ANM=2(∠P+∠Q)=88°,
∴ ∠P+∠Q=44°,
∴ ∠BAE=136°.故选 A.

A 【解析】如图,作点 A 关于 BC 的对称点 P,关于 DE 的对称点 Q,连接 PQ 与 BC 相交于点 M,与 DE 相交于点 N,则 AM=PM,AN=QN,
∴ ∠P=∠PAM,∠Q=∠QAN,
∴ △AMN 周长为 AM+MN+AN=PM+MN+QN≥PQ,
∴ 当 P,M,N,Q 在一条直线上时,PQ 的长度即为△AMN 周长的最小值.
∵ ∠AMN=∠P+∠PAM=2∠P,∠ANM=∠Q+∠QAN=2∠Q,
∴ ∠AMN+∠ANM=2(∠P+∠Q)=88°,
∴ ∠P+∠Q=44°,
∴ ∠BAE=136°.故选 A.

6 如图,在等边$\triangle ABC$中,$D$,$E分别为AB$,$AC$边上的动点,$BD= 2AE$,连接$DE$,以$DE为边在\triangle ABC内作等边\triangle DEF$,连接$CF$,当点$D从点A向点B$运动(不运动到点$B$)时,$\angle ECF$大小的变化情况是( )

A.不变
B.变小
C.变大
D.先变大后变小

A.不变
B.变小
C.变大
D.先变大后变小
答案:
A 【解析】在 AC 上截取 CN=AE,连接 FN,如图所示.
∵ △ABC 是等边三角形,
∴ ∠A=60°,AB=AC.
∵ BD=2AE,
∴ AD=EN.
∵ △DEF 是等边三角形,
∴ DE=EF,∠DEF=60°.
∵ ∠ADE=180° - ∠A - ∠AED=180° - 60° - ∠AED=120° - ∠AED,∠NEF=180° - ∠DEF - ∠AED=180° - 60° - ∠AED=120° - ∠AED,
∴ ∠ADE=∠NEF.在△ADE 和△NEF 中,{AD=EN,∠ADE=∠NEF,DE=EF},
∴ △ADE≌△NEF(SAS),
∴ AE=FN,∠FNE=∠A=60°,
∴ FN=CN,
∴ ∠NCF=∠NFC.
∵ ∠FNE=∠NCF+∠NFC=60°,
∴ ∠NCF=30°,即∠ECF=30°.故选 A.

A 【解析】在 AC 上截取 CN=AE,连接 FN,如图所示.
∵ △ABC 是等边三角形,
∴ ∠A=60°,AB=AC.
∵ BD=2AE,
∴ AD=EN.
∵ △DEF 是等边三角形,
∴ DE=EF,∠DEF=60°.
∵ ∠ADE=180° - ∠A - ∠AED=180° - 60° - ∠AED=120° - ∠AED,∠NEF=180° - ∠DEF - ∠AED=180° - 60° - ∠AED=120° - ∠AED,
∴ ∠ADE=∠NEF.在△ADE 和△NEF 中,{AD=EN,∠ADE=∠NEF,DE=EF},
∴ △ADE≌△NEF(SAS),
∴ AE=FN,∠FNE=∠A=60°,
∴ FN=CN,
∴ ∠NCF=∠NFC.
∵ ∠FNE=∠NCF+∠NFC=60°,
∴ ∠NCF=30°,即∠ECF=30°.故选 A.

7 [2025福建泉州期中]如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,点$D在边AB$上,$AD= AC$,点$E在BC$边上,$CE= BD$,过点$E作EF\perp CD交AB于点F$,若$AF= 2$,$BC= 8$,则$DF$的长为( )

A.$3.8$
B.$4$
C.$4.2$
D.$5$

A.$3.8$
B.$4$
C.$4.2$
D.$5$
答案:
B 【解析】延长 AC 到点 G,使 AG=AB,连接 BG,延长 CA,EF 交于点 H,设 EF 和 CD 交于点 K,如图.设∠BCD=α.
∵ ∠ACB=90°,
∴ ∠ACD=90° - α.
∵ AD=AC,
∴ ∠ADC=∠ACD=90° - α,
∴ ∠CAB=180° - 2∠ACD=2α,
∴ ∠ABC=90° - 2α.
∵ EF⊥CD,
∴ ∠CKF=90°,
∴ ∠DFK=90° - (90° - α)=α.
∵ ∠CEF 是△BEF 的外角,
∴ ∠CEF=∠ABC+∠DFK=90° - α.
∵ AD=AC,AG=AB,
∴ ∠ABG=∠G=$\frac{1}{2}$×(180° - ∠CAB)=90° - α,BD=CG=CE,
∴ ∠G=∠CEF.
∵ ∠H+∠DCH=90°,∠BCD+∠DCH=90°,
∴ ∠H=∠BCD=α.
∵ ∠CAB=2α,
∴ ∠AFH=α,
∴ ∠H=∠AFH,
∴ AH=AF=2.在△CEH 和△CGB 中,{∠CEH=∠G,CE=CG,∠ECH=∠GCB=90°},
∴ △CEH≌△CGB(ASA),
∴ CH=CB=8,
∴ DF=AD - AF=AC - AH=CH - 2AH=8 - 4=4.故选 B.

B 【解析】延长 AC 到点 G,使 AG=AB,连接 BG,延长 CA,EF 交于点 H,设 EF 和 CD 交于点 K,如图.设∠BCD=α.
∵ ∠ACB=90°,
∴ ∠ACD=90° - α.
∵ AD=AC,
∴ ∠ADC=∠ACD=90° - α,
∴ ∠CAB=180° - 2∠ACD=2α,
∴ ∠ABC=90° - 2α.
∵ EF⊥CD,
∴ ∠CKF=90°,
∴ ∠DFK=90° - (90° - α)=α.
∵ ∠CEF 是△BEF 的外角,
∴ ∠CEF=∠ABC+∠DFK=90° - α.
∵ AD=AC,AG=AB,
∴ ∠ABG=∠G=$\frac{1}{2}$×(180° - ∠CAB)=90° - α,BD=CG=CE,
∴ ∠G=∠CEF.
∵ ∠H+∠DCH=90°,∠BCD+∠DCH=90°,
∴ ∠H=∠BCD=α.
∵ ∠CAB=2α,
∴ ∠AFH=α,
∴ ∠H=∠AFH,
∴ AH=AF=2.在△CEH 和△CGB 中,{∠CEH=∠G,CE=CG,∠ECH=∠GCB=90°},
∴ △CEH≌△CGB(ASA),
∴ CH=CB=8,
∴ DF=AD - AF=AC - AH=CH - 2AH=8 - 4=4.故选 B.

如图,$\triangle ABC的外角\angle ACF$,$\angle EAC的平分线CP$,$AP交于点P$,连接$BP$,过点$P作PM\perp BE$,$PN\perp BF$,垂足分别为$M$,$N$。下列结论中正确的个数是( )

A.$1$个
B.$2$个
C.$3$个
D.$4$个
D

A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
D 【解析】过 P 作 PQ⊥AC 于 Q.
∵ ∠ACF,∠EAC 的平分线 CP,AP 交于点 P,PM⊥BE,PN⊥BF,
∴ PM=PQ,PQ=PN,
∴ PM=PN,
∴ P 在∠ABC 的平分线上,即 BP 平分∠ABC,故①正确.
∵ PM⊥BE,PN⊥BF,PQ⊥AC,
∴ ∠PMA=∠PQA=90°,∠PQC=∠PNC=90°.在 Rt△PMA 和 Rt△PQA 中,{PA=PA,PM=PQ},
∴ Rt△PMA≌Rt△PQA(HL),
∴ ∠MPA=∠QPA,同理 Rt△PQC≌Rt△PNC,
∴ ∠QPC=∠NPC,
∴ ∠MPN=2∠APC.
∵ ∠PMA=∠PNC=90°,
∴ ∠ABC+∠MPN=360° - 90° - 90°=180°,
∴ ∠ABC+2∠APC=180°,故②正确.
∵ CP 平分∠FCA,BP 平分∠ABC,
∴ ∠FCA=∠ABC+∠CAB=2∠PCN,∠PCN=$\frac{1}{2}$∠ABC+∠CPB,
∴ ∠ABC+∠CAB=2($\frac{1}{2}$∠ABC+∠CPB),
∴ ∠CAB=2∠CPB,故③正确.
∵ Rt△PMA≌Rt△PQA,Rt△PQC≌Rt△PNC,
∴ S△PAC=S△MAP+S△NCP,故④正确.即正确的个数是 4 个,故选 D.
∵ ∠ACF,∠EAC 的平分线 CP,AP 交于点 P,PM⊥BE,PN⊥BF,
∴ PM=PQ,PQ=PN,
∴ PM=PN,
∴ P 在∠ABC 的平分线上,即 BP 平分∠ABC,故①正确.
∵ PM⊥BE,PN⊥BF,PQ⊥AC,
∴ ∠PMA=∠PQA=90°,∠PQC=∠PNC=90°.在 Rt△PMA 和 Rt△PQA 中,{PA=PA,PM=PQ},
∴ Rt△PMA≌Rt△PQA(HL),
∴ ∠MPA=∠QPA,同理 Rt△PQC≌Rt△PNC,
∴ ∠QPC=∠NPC,
∴ ∠MPN=2∠APC.
∵ ∠PMA=∠PNC=90°,
∴ ∠ABC+∠MPN=360° - 90° - 90°=180°,
∴ ∠ABC+2∠APC=180°,故②正确.
∵ CP 平分∠FCA,BP 平分∠ABC,
∴ ∠FCA=∠ABC+∠CAB=2∠PCN,∠PCN=$\frac{1}{2}$∠ABC+∠CPB,
∴ ∠ABC+∠CAB=2($\frac{1}{2}$∠ABC+∠CPB),
∴ ∠CAB=2∠CPB,故③正确.
∵ Rt△PMA≌Rt△PQA,Rt△PQC≌Rt△PNC,
∴ S△PAC=S△MAP+S△NCP,故④正确.即正确的个数是 4 个,故选 D.
9 [2024江苏徐州质检]如图,在$\triangle ABC$中,$\angle B= \angle C= 70^{\circ}$,$AD平分\angle BAC$,$E是AC$上一点,且$\angle ADE= \angle AED$,则$\angle CDE$的度数是____
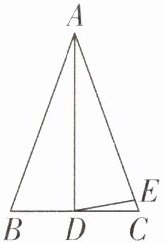
10°
。
答案:
10° 【解析】
∵ ∠B=∠C=70°,
∴ ∠BAC=180° - ∠B - ∠C=40°.
∵ AD 平分∠BAC,
∴ ∠CAD=$\frac{1}{2}$∠BAC=20°,
∴ ∠ADC=180° - ∠CAD - ∠C=90°.
∵ AD=AE,
∴ ∠ADE=∠AED=$\frac{1}{2}$(180° - ∠CAD)=80°,
∴ ∠CDE=∠ADC - ∠ADE=10°.故答案为 10°.
∵ ∠B=∠C=70°,
∴ ∠BAC=180° - ∠B - ∠C=40°.
∵ AD 平分∠BAC,
∴ ∠CAD=$\frac{1}{2}$∠BAC=20°,
∴ ∠ADC=180° - ∠CAD - ∠C=90°.
∵ AD=AE,
∴ ∠ADE=∠AED=$\frac{1}{2}$(180° - ∠CAD)=80°,
∴ ∠CDE=∠ADC - ∠ADE=10°.故答案为 10°.
查看更多完整答案,请扫码查看


