《2025年初中必刷题八年级数学上册苏科版》

如图,将边长为8 cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是(A)
A.3 cm
B.4 cm
C.5 cm
D.6 cm

答案： A [解析]设CN=x cm,则DN=(8 - x)cm.由折叠的性质知EN=DN=(8 - x)cm.
∵ E为BC的中点,
∴ EC= $\frac{1}{2}$BC=4 cm.在Rt△ECN中,由勾股定理可知EN²=EC²+CN²,即(8 - x)²=4²+x²,
∴ x=3.故选A.

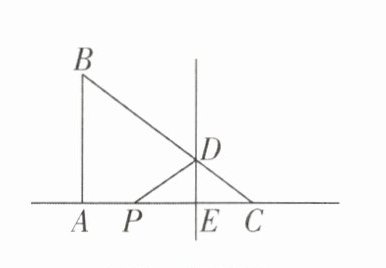
2 [2025江苏苏州质检,较难]如图,$Rt\triangle ABC$中,$\angle BAC= 90^{\circ },AC= 12,AB= 9,DE\perp AC,CD= \frac {1}{3}BC,CE= \frac {1}{3}AC$,P是直线AC上一点,把$\triangle CDP$沿DP所在的直线翻折后,点C落在直线DE上的点H处,则$CP= $( )


A.10
B.$\frac {5}{2}$
C.8或$\frac {5}{2}$
D.10或$\frac {5}{2}$

答案：
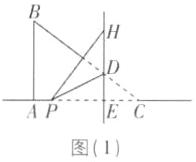
D [解析]当P点在E点左边时,如图
(1)所示.
∵ 把△CDP沿DP所在的直线翻折后,点C落在直线DE上的点H处,
∴ PC=PH,DC=DH.
∵ ∠BAC=90°,AC=12,AB=9,
∴ BC²=AB²+AC²=9²+12²=225,
∴ BC=15.
∵ DH=CD= $\frac{1}{3}$BC= $\frac{1}{3}$×15=5,CE= $\frac{1}{3}$AC= $\frac{1}{3}$×12=4,DE⊥AC,
∴ DE²=CD² - EC²=9,
∴ DE=3,
∴ EH=DE+DH=3+5=8.设PC=x,则PH=x,PE=x - 4.
∵ PH² - PE²=EH²,
∴ x² - (x - 4)²=8²,解得x=10,即CP=10.

当P点在E点右边时,如图
(2)所示.同理可得DH=CD=5,CE=4,
∴ DE=3,
∴ EH=DH - ED=5 - 3=2.设PC=a,则PE=EC - PC=4 - a,PH=a.
∵ PH² - PE²=EH²,
∴ a² - (4 - a)²=2²,解得a= $\frac{5}{2}$,即PC= $\frac{5}{2}$.综上所述,PC= $\frac{5}{2}$或10.故选D.

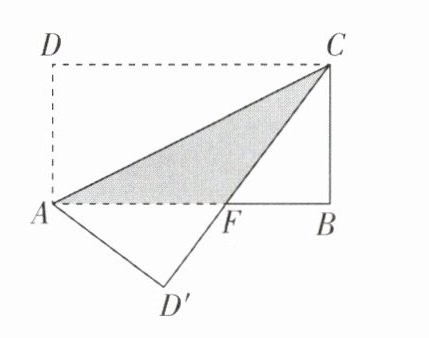
3 [2024江苏泰州质检,中]如图,长方形ABCD中,$AB= 8,BC= 4$,将长方形沿AC折叠,点D落在点$D'$处,则重叠部分$\triangle AFC$的面积为____10.

答案： 10 [解析]易得AD'=4,△AFD'≌△CFB,
∴ D'F=BF.设D'F=BF=x,则AF=8 - x.在Rt△AFD'中,(8 - x)²=x²+4²,解得x=3,
∴ AF=8 - 3=5,
∴ S△AFC= $\frac{1}{2}$AF·BC=10.故答案为10.

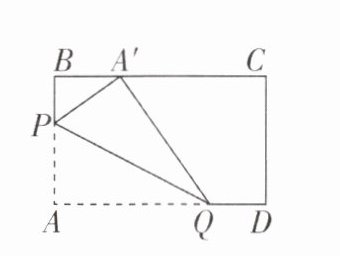
4 [2024浙江金华义乌调研,中]如图所示,在长方形纸片ABCD中,$AB= 3,BC= 5$.折叠纸片使点A落在边BC上的$A'$处,折痕为PQ.当点$A'$在边BC上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在边AB,AD上移动,则点$A'$在边BC上可移动的最大距离为____.

答案：
2 [解析]当点P与B重合时,BA'取最大值,是3.当点Q与D重合时,如图所示.由折叠的性质得A'D=AD.
∵ 四边形ABCD是长方形,
∴ AD=BC=5,CD=AB=3,∠C=90°,
∴ A'D=AD=5.由勾股定理得A'C²=A'D² - CD²=5² - 3²=4²,则A'C=4,此时BA'取得最小值,为1,则点A'在边BC上可移动的最大距离为3 - 1=2.故答案为2.

5 [2024江苏扬州期中,中]如图,长方体的底面的宽与长分别为2 cm和4 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )

A.10 cm
B.11 cm
C.13 cm
D.17 cm

答案：
C [解析]长方体的侧面展开图如图所示.
∵ 长方体的底面的宽与长分别为2 cm和4 cm,高为5 cm,
∴ PA=2+4+2+4=12(cm),QA=5 cm,
∴ PQ²=PA²+AQ²=13²,则PQ=13 cm,即蚂蚁爬行的最短路径长为13 cm.故选C.

6 [2024江苏苏州调研,较难]如图所示,有一块长方形场地ABCD,长$AB= 20m$,宽$AD= 10m$,中间竖有一堵墙,高$MN= 2m$,一只蚂蚁要从A点爬到C点,它必须翻过中间那堵墙,则它至少要爬( )


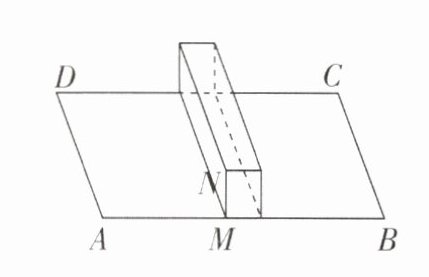
A.20 m
B.24 m
C.25 m
D.26 m

答案：
D [解析]如图所示,将题图展开,长方形ABCD的长增加2个MN的长度,即原图长度增加4米,
∴ AB=20+4=24(米).
∵ 四边形ABCD是长方形,AB=24米,AD=10米,
∴ BC=AD=10米,∠ABC=90°,
∴ 在Rt△ABC中,由勾股定理得AC²=AB²+BC²=24²+10²=676,
∴ AC=26米,
∴ 蚂蚁从A点爬到C点,它至少要爬26米.故选D.

7 [中]如图,圆柱形玻璃杯的杯高为9 cm,底面周长为16 cm,在杯内壁离杯底4 cm的点A处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1 cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所走的最短路程为____cm.(杯壁厚度不计)

答案：
10 [解析]如图,将杯子侧面的一半展开,作B关于EF的对称点B',连接B'A,则B'A的长即为最短路程,过点B'作B'D⊥AE交AE的延长线于D.根据题意可得AD=9 - 4+1=6(cm),B'D= $\frac{1}{2}$×16=8(cm),
∴ B'A²=B'D²+AD²=8²+6²=10²,则B'A=10 cm,故答案为10.