第84页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
10 传统文化 《九章算术》 (2024·苏州期中)《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的$B'$,示意图如图,则水深为
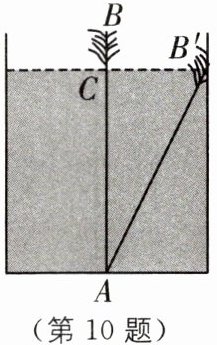
12
尺.
答案:
12
11 新情境 放风筝 (2025·徐州铜山区期中)长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE.
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
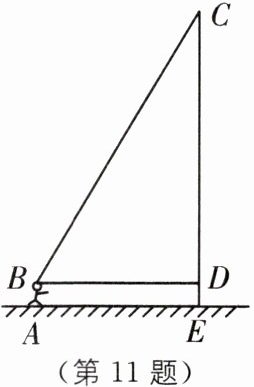
(1)求风筝的垂直高度CE.
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?

答案:
(1)在$Rt\triangle CDB$中,由勾股定理,得$CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{25^{2}-15^{2}}=20$(米),所以$CE = CD + DE = 20 + 1.6 = 21.6$(米).故风筝的垂直高度CE为21.6米.
(2)如图,由题意,得$CM = 12$米,

$\therefore DM = CD - CM = 8$米,$\therefore BM=\sqrt{DM^{2}+BD^{2}}=17$米,$\therefore BC - BM = 25 - 17 = 8$(米).故他应该往回收线8米.
(1)在$Rt\triangle CDB$中,由勾股定理,得$CD=\sqrt{BC^{2}-BD^{2}}=\sqrt{25^{2}-15^{2}}=20$(米),所以$CE = CD + DE = 20 + 1.6 = 21.6$(米).故风筝的垂直高度CE为21.6米.
(2)如图,由题意,得$CM = 12$米,

$\therefore DM = CD - CM = 8$米,$\therefore BM=\sqrt{DM^{2}+BD^{2}}=17$米,$\therefore BC - BM = 25 - 17 = 8$(米).故他应该往回收线8米.
(1)对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:$3^{2}+4^{2}= 5^{2}$,若把它扩大2倍、3倍,就分别得到$6^{2}+8^{2}= 10^{2}和9^{2}+12^{2}= 15^{2}$,…,若把它扩大11倍,就得到
(2)对于任意一个大于1的奇数,存在下列勾股数:
若勾股数为3,4,5,因为$3^{2}= 5^{2}-4^{2}$,则有$3^{2}= 4+5$;
若勾股数为5,12,13,则有$5^{2}= 12+13$;
①若勾股数为7,24,25,则有
②若勾股数为17,a,b(a<b),根据以上的规律,求a,b的值.
$33^{2}+44^{2}=55^{2}$
,若把它扩大n倍(n为正整数),就得到$(3n)^{2}+(4n)^{2}=(5n)^{2}$
.(2)对于任意一个大于1的奇数,存在下列勾股数:
若勾股数为3,4,5,因为$3^{2}= 5^{2}-4^{2}$,则有$3^{2}= 4+5$;
若勾股数为5,12,13,则有$5^{2}= 12+13$;
①若勾股数为7,24,25,则有
$7^{2}=25 + 24$
;②若勾股数为17,a,b(a<b),根据以上的规律,求a,b的值.
$3^{2}=5^{2}-4^{2}$,$3^{2}=4 + 5$,$5^{2}=13^{2}-12^{2}$,$5^{2}=12 + 13$,$7^{2}=25^{2}-24^{2}$,$7^{2}=49 = 24 + 25$,$\cdots$,以此类推,$(2n + 1)^{2}=(m + 1)^{2}-m^{2}$($m,n$都为正整数),$(2n + 1)^{2}=m + m + 1$,$\therefore 17^{2}=a + b$.$\because a\lt b$,$\therefore b = a + 1$,$\therefore 17^{2}=289 = 2a + 1$,$\therefore a = 144$,$\therefore b = a + 1 = 145$.
答案:
(1)$33^{2}+44^{2}=55^{2}$ $(3n)^{2}+(4n)^{2}=(5n)^{2}$
(2)①$7^{2}=25 + 24$
②$3^{2}=5^{2}-4^{2}$,$3^{2}=4 + 5$,$5^{2}=13^{2}-12^{2}$,$5^{2}=12 + 13$,$7^{2}=25^{2}-24^{2}$,$7^{2}=49 = 24 + 25$,$\cdots$,以此类推,$(2n + 1)^{2}=(m + 1)^{2}-m^{2}$($m,n$都为正整数),$(2n + 1)^{2}=m + m + 1$,$\therefore 17^{2}=a + b$.$\because a\lt b$,$\therefore b = a + 1$,$\therefore 17^{2}=289 = 2a + 1$,$\therefore a = 144$,$\therefore b = a + 1 = 145$.
(1)$33^{2}+44^{2}=55^{2}$ $(3n)^{2}+(4n)^{2}=(5n)^{2}$
(2)①$7^{2}=25 + 24$
②$3^{2}=5^{2}-4^{2}$,$3^{2}=4 + 5$,$5^{2}=13^{2}-12^{2}$,$5^{2}=12 + 13$,$7^{2}=25^{2}-24^{2}$,$7^{2}=49 = 24 + 25$,$\cdots$,以此类推,$(2n + 1)^{2}=(m + 1)^{2}-m^{2}$($m,n$都为正整数),$(2n + 1)^{2}=m + m + 1$,$\therefore 17^{2}=a + b$.$\because a\lt b$,$\therefore b = a + 1$,$\therefore 17^{2}=289 = 2a + 1$,$\therefore a = 144$,$\therefore b = a + 1 = 145$.
查看更多完整答案,请扫码查看


