第33页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
8 如图,点 E,F,G,Q,H 在一条直线上,且 EF= GH,我们知道按如图所作的直线 l 为线段 FG 的垂直平分线. 下列说法正确的是(
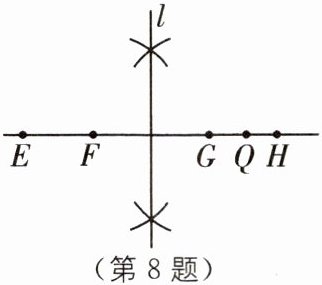
A.l 是线段 EH 的垂直平分线
B.l 是线段 EQ 的垂直平分线
C.l 是线段 FH 的垂直平分线
D.EH 是直线 l 的垂直平分线
A
).
A.l 是线段 EH 的垂直平分线
B.l 是线段 EQ 的垂直平分线
C.l 是线段 FH 的垂直平分线
D.EH 是直线 l 的垂直平分线
答案:
A
9 (2025·重庆渝北区期中)如图,在△ABC 中,∠BAC 的平分线交 BC 于点 D.
(1)用尺规完成以下基本作图:作 AD 的垂直平分线分别与 AB,AC,AD 交于点 E,F,H;(保留作图痕迹,不写作法)
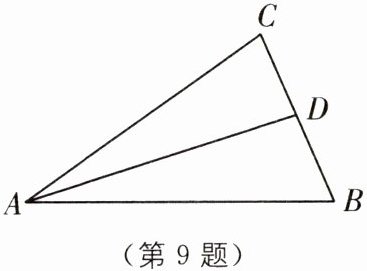
(2)在(1)所作的图形中,连接 DE,DF,完成下面证明 HE= HF 的过程.
证明:∵∠BAC 的平分线交 BC 于点 D,
∴∠BAD= ①______.
∵EF 垂直平分 AD,
∴∠AHF= ∠DHE= 90°,
AH= ②______,
③______,
∴∠BAD= ∠ADE,
∴∠CAD= ∠ADE,
∴△AHF≌④______(ASA),
∴HE= HF.
(1)用尺规完成以下基本作图:作 AD 的垂直平分线分别与 AB,AC,AD 交于点 E,F,H;(保留作图痕迹,不写作法)

(2)在(1)所作的图形中,连接 DE,DF,完成下面证明 HE= HF 的过程.
证明:∵∠BAC 的平分线交 BC 于点 D,
∴∠BAD= ①______.
∵EF 垂直平分 AD,
∴∠AHF= ∠DHE= 90°,
AH= ②______,
③______,
∴∠BAD= ∠ADE,
∴∠CAD= ∠ADE,
∴△AHF≌④______(ASA),
∴HE= HF.
答案:
(1)如图,直线 EF 即为所求.
(2)∠CAD DH AE=DE △DHE
解题关键 本题考查了作图—基本作图、角平分线定义、全等三角形的判定和性质、线段垂直平分线的性质,正确地作出图形是解题的关键.

(1)如图,直线 EF 即为所求.
(2)∠CAD DH AE=DE △DHE
解题关键 本题考查了作图—基本作图、角平分线定义、全等三角形的判定和性质、线段垂直平分线的性质,正确地作出图形是解题的关键.

10 中考新考法 开放探究(2025·广西防城港防城区期中)
[概念理解]
如图(1),在四边形 ABCD 中,AD= CD,AB= CB. 我们把这种两组邻边分别相等的四边形叫作“筝形”.
[性质探究]
(1)如图(1),连接筝形 ABCD 的对角线 AC,BD 交于点 O,试探究筝形 ABCD 的性质,并填空:
对角线 AC,BD 的位置关系是:
AO 与 CO 的数量关系是:
[知识应用]
如图(2),秀秀想要做一个“筝形”风筝,她先固定中间的“十字架”,再确定四周.
(2)①从数学的角度看,秀秀确定“十字架”对角线 EG 和 HF 时应满足的条件是
②借助图(2)以及①中所写条件,说明四边形 EHGF 是个“筝形”.
[应用拓展]
(3)在“筝形”风筝 EHGF 中,已知 EG= 60 cm,HF= 40 cm,求“筝形”风筝 EHGF 的面积.
[概念理解]
如图(1),在四边形 ABCD 中,AD= CD,AB= CB. 我们把这种两组邻边分别相等的四边形叫作“筝形”.
[性质探究]
(1)如图(1),连接筝形 ABCD 的对角线 AC,BD 交于点 O,试探究筝形 ABCD 的性质,并填空:
对角线 AC,BD 的位置关系是:
AC⊥BD
;AO 与 CO 的数量关系是:
AO=CO
.[知识应用]
如图(2),秀秀想要做一个“筝形”风筝,她先固定中间的“十字架”,再确定四周.
(2)①从数学的角度看,秀秀确定“十字架”对角线 EG 和 HF 时应满足的条件是
EG 垂直平分 HF
;②借助图(2)以及①中所写条件,说明四边形 EHGF 是个“筝形”.
∵EG 垂直平分 HF,
∴EH=EF,GH=GF,
∴四边形 EHGF 是个“筝形”.
∴EH=EF,GH=GF,
∴四边形 EHGF 是个“筝形”.
[应用拓展]
(3)在“筝形”风筝 EHGF 中,已知 EG= 60 cm,HF= 40 cm,求“筝形”风筝 EHGF 的面积.
∵四边形 EHGF 是筝形,
∴EG⊥HF,
∴“筝形”风筝 EHGF 的面积=△EHF 的面积+△HGF 的面积= $\frac{1}{2}$HF·EI+$\frac{1}{2}$HF·IG=$\frac{1}{2}$HF·(EI+IG)=$\frac{1}{2}$HF·EG=$\frac{1}{2}$×40×60=1200(cm²).
∴EG⊥HF,
∴“筝形”风筝 EHGF 的面积=△EHF 的面积+△HGF 的面积= $\frac{1}{2}$HF·EI+$\frac{1}{2}$HF·IG=$\frac{1}{2}$HF·(EI+IG)=$\frac{1}{2}$HF·EG=$\frac{1}{2}$×40×60=1200(cm²).
答案:
(1)AC⊥BD AO=CO
(2)①EG 垂直平分 HF
②
∵EG 垂直平分 HF,
∴EH=EF,GH=GF,
∴四边形 EHGF 是个“筝形”.
(3)
∵四边形 EHGF 是筝形,
∴EG⊥HF,
∴“筝形”风筝 EHGF 的面积=△EHF 的面积+△HGF 的面积= $\frac{1}{2}$HF·EI+$\frac{1}{2}$HF·IG=$\frac{1}{2}$HF·(EI+IG)=$\frac{1}{2}$HF·EG=$\frac{1}{2}$×40×60=1200(cm²).
归纳总结 本题考查了线段垂直平分线的性质、三角形的面积,正确地理解筝形是解题的关键.
(1)AC⊥BD AO=CO
(2)①EG 垂直平分 HF
②
∵EG 垂直平分 HF,
∴EH=EF,GH=GF,
∴四边形 EHGF 是个“筝形”.
(3)
∵四边形 EHGF 是筝形,
∴EG⊥HF,
∴“筝形”风筝 EHGF 的面积=△EHF 的面积+△HGF 的面积= $\frac{1}{2}$HF·EI+$\frac{1}{2}$HF·IG=$\frac{1}{2}$HF·(EI+IG)=$\frac{1}{2}$HF·EG=$\frac{1}{2}$×40×60=1200(cm²).
归纳总结 本题考查了线段垂直平分线的性质、三角形的面积,正确地理解筝形是解题的关键.
查看更多完整答案,请扫码查看


