第38页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 教材 P53习题T3·变式 等腰三角形的一个内角是50°,则另外两个角的度数分别是(
A.65°,65°
B.50°,80°
C.65°,65°或50°,80°
D.50°,50°
C
).A.65°,65°
B.50°,80°
C.65°,65°或50°,80°
D.50°,50°
答案:
C
如图,在△ABC 中,AB= AC,∠A= 30°,直线a//b,顶点 C 在直线b 上,直线a 交 AB 于点 D,交 AC 于点 E,若∠1= 145°,则∠2 的度数是(
A.30°
B.35°
C.40°
D.45°
C
).A.30°
B.35°
C.40°
D.45°
答案:
C
3 教材 P49习题T1·变式 若等腰三角形的两边长分别为2和5,则它的周长为(
A.9
B.7
C.12
D.9或12
C
).A.9
B.7
C.12
D.9或12
答案:
C
4 教材 P43例1·变式 (2025·湖北武汉东西湖区期末)如图,AB= AC,∠A= 40°,AB 的垂直平分线 MN 交 AC 于点 D,则∠DBC 的度数是(
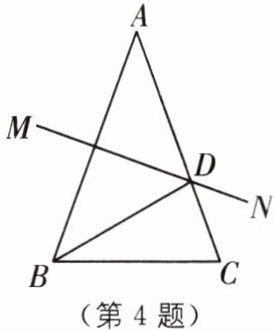
A.20°
B.30°
C.40°
D.50°
B
).
A.20°
B.30°
C.40°
D.50°
答案:
B
5 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫作“倍长三角形”.若等腰三角形 ABC 是“倍长三角形”,底边 BC 的长为4,则腰 AB 的长为
8
.
答案:
8 [解析]
∵△ABC是等腰三角形,
∴AB=AC.
∵△ABC是“倍长三角形”,BC=4,①当AB=AC=2BC时,AB=AC=8;②当BC=2AB=2AC时,AB=AC=2,根据三角形三边关系,此时,不能构成三角形,不符合题意,
∴若等腰三角形ABC是“倍长三角形”,底边BC的长为4,则腰AB的长为8.
∵△ABC是等腰三角形,
∴AB=AC.
∵△ABC是“倍长三角形”,BC=4,①当AB=AC=2BC时,AB=AC=8;②当BC=2AB=2AC时,AB=AC=2,根据三角形三边关系,此时,不能构成三角形,不符合题意,
∴若等腰三角形ABC是“倍长三角形”,底边BC的长为4,则腰AB的长为8.
6 教材 P49习题T4·改编 在△ABC 中,AB= AC,∠BAC= 100°,点 D 在边 BC 上,连接 AD,若△ABD 为直角三角形,则∠ADB 的度数是
90°或50°
.
答案:
90°或50°
7 (2025·徐州期中)如图,在△ABC 中,AB= AC,点 D 在 BC 上,DE⊥AB,DF⊥AC,垂足分别为 E,F,且 DE= DF.求证:D 是 BC 的中点.
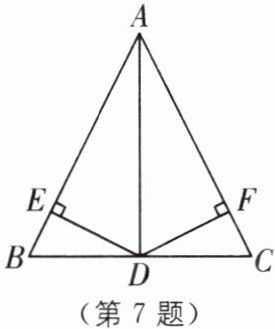

答案:
∵DE⊥AB,DF⊥AC,且DE=DF,
∴AD是∠BAC的平分线.
∵在△ABC中,AB=AC,
∴D是BC的中点.思路引导 本题考查了角平分线的性质和等腰三角形三线合一的性质,解题的关键是证得AD是∠BAC的平分线.
∵DE⊥AB,DF⊥AC,且DE=DF,
∴AD是∠BAC的平分线.
∵在△ABC中,AB=AC,
∴D是BC的中点.思路引导 本题考查了角平分线的性质和等腰三角形三线合一的性质,解题的关键是证得AD是∠BAC的平分线.
8 (2025·山东济宁期中)在△ABC 中,AB= 20,BC= 8,AC= 2m-2.
(1)求 m 的取值范围;
(2)若△ABC 是等腰三角形,求△ABC 的周长.
(1)求 m 的取值范围;
(2)若△ABC 是等腰三角形,求△ABC 的周长.
答案:
(1)在△ABC中,AB=20,BC=8,AC=2m−2,
∴20−8<2m−2<20+8,解得7<m<15,
∴m的取值范围为7<m<15.
(2)
∵△ABC是等腰三角形,
∴分两种情况:①当AB=AC=20时,△ABC的周长=20+20+8=48;②当BC=AC=8时,
∵8+8=16<20,
∴不能组成三角形.综上所述,△ABC的周长为48.
(1)在△ABC中,AB=20,BC=8,AC=2m−2,
∴20−8<2m−2<20+8,解得7<m<15,
∴m的取值范围为7<m<15.
(2)
∵△ABC是等腰三角形,
∴分两种情况:①当AB=AC=20时,△ABC的周长=20+20+8=48;②当BC=AC=8时,
∵8+8=16<20,
∴不能组成三角形.综上所述,△ABC的周长为48.
9 在△ABC 和△A'B'C'中,∠B= ∠B'= 30°,AB= A'B'= 6,AC= A'C'= 4,若∠C= n°,则∠C'= (
A.30°
B.n°
C.n°或180°-n°
D.30°或150°
C
).A.30°
B.n°
C.n°或180°-n°
D.30°或150°
答案:
C
10 (2025·南京秦淮区期中)如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆 DE 上一点 A 往地面拉两条长度相等的固定绳 AB 和 AC,当点 B,E,C 在同一直线上且固定点 B,C 到杆脚 E 的距离相等时,电线杆 DE 就垂直于 BC,工程人员这种操作方法的依据是(
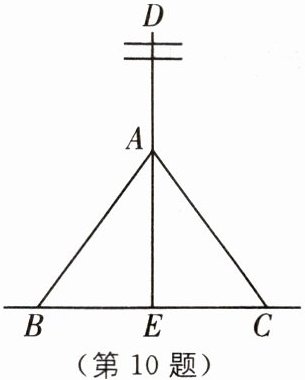
A.等边对等角
B.垂线段最短
C.线段垂直平分线上的点到线段两端的距离相等
D.等腰三角形底边上的高线,中线及顶角平分线重合
D
).
A.等边对等角
B.垂线段最短
C.线段垂直平分线上的点到线段两端的距离相等
D.等腰三角形底边上的高线,中线及顶角平分线重合
答案:
D
查看更多完整答案,请扫码查看


