《2025年课时训练江苏人民出版社八年级数学上册苏科版》

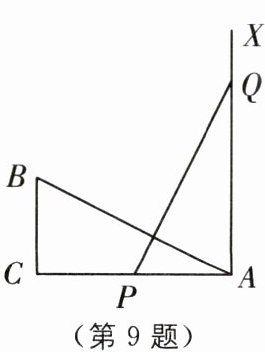
9(2024·山东济南天桥区期末)如图,∠C= 90°,AC= 10,BC= 5,AX⊥AC,点P和点Q从点A出发,分别在线段AC和射线AX上运动,且AB= PQ(不考虑PQ= 0的情况),当点P运动到AP= 5或10时,△ABC与△APQ全等.

答案： 5或10

10 求证：有一条直角边及斜边上的高对应相等的两个直角三角形全等.

答案：
如图,已知在Rt△ABC和Rt△A'B'C'中,
∠ACB = ∠A'C'B' = 90°,CD⊥AB于点D,C'D'⊥A'B’于点D',BC = B'C',CD = C'D'.
求证:Rt△ABC≌Rt△A'B'C'.
　　　　　　　
证明:
∵CD⊥AB于点D,C'D'⊥A'B'于点D',
∴∠CDB = ∠C'D'B' = 90°.
在Rt△CDB与Rt△C'D'B'中,{BC = B'C', CD = C'D',
∴Rt△CDB≌Rt△C'D'B'(HL),
∴∠B = ∠B'.
在Rt△ABC和Rt△A'B'C'中,
∠ACB = ∠A'C'B' = 90°,
BC = B'C',
∠B = ∠B',
∴Rt△ABC≌Rt△A'B'C'(ASA).
思路引导　此题主要考查学生对直角三角形全等的判定的理解和掌握,解题的关键是先证△CDB≌△C'D'B',得到∠B = ∠B',然后利用ASA即可证明Rt△ABC≌Rt△A'B'C'.

11(2024·湖南岳阳华容期末)如图,BD,CE分别是△ABC的高,且BE= CD,求证：Rt△BEC≌Rt△CDB.
]

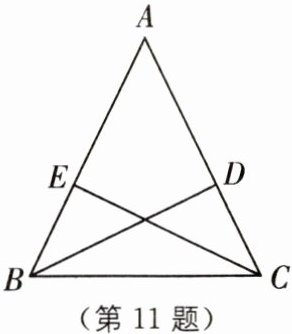
答案：
∵BD,CE分别是△ABC的高，
∴∠BEC = ∠CDB = 90°.
在Rt△BEC和Rt△CDB中,{BC = CB, BE = CD,
∴Rt△BEC≌Rt△CDB(HL).

12 如图,AB= BC,∠BAD= ∠BCD= 90°,点D是EF上一点,AE⊥EF于点E,CF⊥EF于点F,AE= CF,求证：Rt△ADE≌Rt△CDF.
]

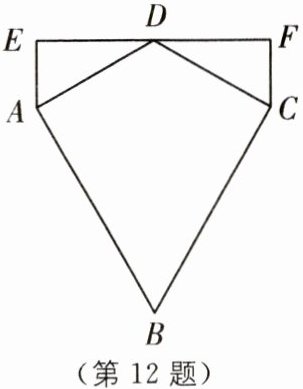
答案：
如图，连接BD,
∵∠BAD = ∠BCD = 90°,
∴在Rt△ABD和Rt△CBD中,{AB = CB, BD = BD,
　　　　　　　　　　　　　　　　
∴Rt△ABD≌Rt△CBD(HL),
∴AD = CD.
∵AE⊥EF于点E,CF⊥EF于点F,
∴∠E = ∠F = 90°,
在Rt△ADE和Rt△CDF中,{AE = CF, AD = CD,
∴Rt△ADE≌Rt△CDF(HL).

13 如图,在Rt△ABC中,∠A= 90°,在边BC上取点D,使得CD= CA,过点D作DE⊥BC交AB于点E. 若AB= 10,DE= 4,求BE的长.
]

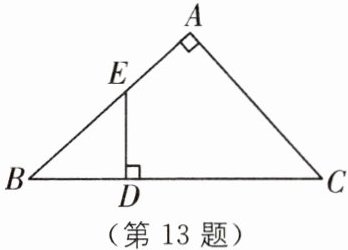
答案： 连接CE.
在Rt△AEC和Rt△DEC中,{CA = CD, CE = CE,
∴Rt△AEC≌Rt△DEC(HL),
∴AE = DE.
∵DE = 4,
∴AE = 4.
∵AB = 10,
∴BE = AB−AE = 10−4 = 6.

14 角平分线模型(2025·无锡江阴期中)在Rt△ABC中,∠ABC= 90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE. AC= DE,BC= BE.
(1)求证：AB= BD.
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG. 当KB平分∠AKG时,求证：AK= DG+KG.
]

答案：

(1)在Rt△ACB和Rt△DEB中,{AC = DE, BC = BE,
∴Rt△ACB≌Rt△DEB(HL),
∴AB = BD.
(2)如图,作BM平分∠ABD交AK于点M.
∵BM平分∠ABD,KB平分∠AKG,BF平分∠ABC,
　　　　　　　　　　　　　　　　
∴∠ABM = ∠MBD = 45°,
∠AKB = ∠BKG,
∠ABF = ∠FBC = 45°.
∵∠FBC = ∠DBG = 45°,
∴∠MBD = ∠GBD.
在△BMK和△BGK中,{∠MBK = ∠GBK, BK = BK, ∠MKB = ∠GKB,
∴△BMK≌△BGK(ASA),
∴BM = BG,MK = KG.
在△ABM和△DBG中,{AB = DB, ∠ABM = ∠DBG, BM = BG,
∴△ABM≌△DBG(SAS),
∴AM = DG.
∵AK = AM + MK,
∴AK = DG + KG.