第76页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
11 传统文化 《九章算术》 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数 a,b,c,其中 a,b 均小于 c,a= $\frac{1}{2}m^{2}-\frac{1}{2}$,c= $\frac{1}{2}m^{2}+\frac{1}{2}$,m 是大于 1 的奇数,则 b=
m
(用含 m 的式子表示).
答案:
m
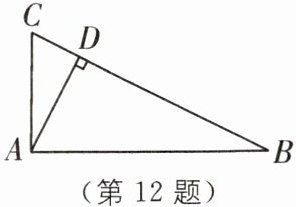
12 如图,在△ABC 中,AD⊥BC,垂足为 D,若 CD= 1,AD= 2,BD= 4,试判断△ABC 的形状,并说明理由.
]
]

答案:
∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∵CD=1,AD=2,BD=4,
∴根据勾股定理,得AC²=5,AB²=20.
∵BC²=(1+4)²=25,
∴AC²+AB²=BC²,
∴△ABC是直角三角形.
∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∵CD=1,AD=2,BD=4,
∴根据勾股定理,得AC²=5,AB²=20.
∵BC²=(1+4)²=25,
∴AC²+AB²=BC²,
∴△ABC是直角三角形.
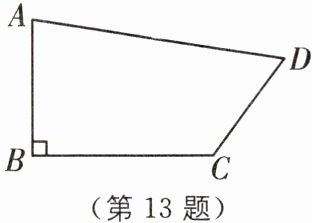
13 教材 P95 练习 T2·改编 (2025·扬州江都区期中)如图,有一张四边形纸片 ABCD,AB⊥BC.经测得 AB= 9 cm,BC= 12 cm,CD= 8 cm,AD= 17 cm.
(1)求 A,C 两点之间的距离;
(2)求这张纸片的面积.
]
(1)求 A,C 两点之间的距离;
(2)求这张纸片的面积.
]

答案:
(1)如图,连接AC.

在Rt△ABC中,AB⊥BC,AB=9 cm,BC=12 cm,
∴AC=√(AB²+BC²)=√(9²+12²)=15(cm).
故A,C两点之间的距离为15 cm.
(2)
∵CD²+AC²=8²+15²=17²=AD²,
∴∠ACD=90°,
∴四边形纸片ABCD的面积=S△ABC+S△ACD
=1/2AB·BC+1/2AC·CD
=1/2×9×12+1/2×15×8
=54+60=114(cm²).
(1)如图,连接AC.

在Rt△ABC中,AB⊥BC,AB=9 cm,BC=12 cm,
∴AC=√(AB²+BC²)=√(9²+12²)=15(cm).
故A,C两点之间的距离为15 cm.
(2)
∵CD²+AC²=8²+15²=17²=AD²,
∴∠ACD=90°,
∴四边形纸片ABCD的面积=S△ABC+S△ACD
=1/2AB·BC+1/2AC·CD
=1/2×9×12+1/2×15×8
=54+60=114(cm²).
14 如图,在△ABC 中,AB= 10,AC= 6,BC= 8,点 D 是 AB 的中点,连接 CD.
(1)若∠B= 50°,求∠DCA 的度数;
(2)若点 E 是 AB 上的一个动点,则线段 CE 的最小值为
]
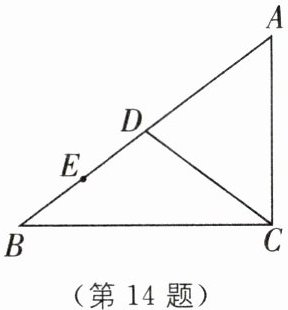
(1)∵AB=10,AC=6,BC=8,
∴AC²+BC²=6²+8²=100,AB²=10²=100,
∴AC²+BC²=AB²,
∴△ABC是直角三角形,
∴∠ACB=90°.
∵点D是AB的中点,
∴CD=DB=1/2AB,
∴∠B=∠DCB=50°,
∴∠DCA=∠ACB-∠DCB=40°.
故∠DCA的度数为40°.
(1)若∠B= 50°,求∠DCA 的度数;
(2)若点 E 是 AB 上的一个动点,则线段 CE 的最小值为
4.8
.]

(1)∵AB=10,AC=6,BC=8,
∴AC²+BC²=6²+8²=100,AB²=10²=100,
∴AC²+BC²=AB²,
∴△ABC是直角三角形,
∴∠ACB=90°.
∵点D是AB的中点,
∴CD=DB=1/2AB,
∴∠B=∠DCB=50°,
∴∠DCA=∠ACB-∠DCB=40°.
故∠DCA的度数为40°.
答案:
(1)
∵AB=10,AC=6,BC=8,
∴AC²+BC²=6²+8²=100,AB²=10²=100,
∴AC²+BC²=AB²,
∴△ABC是直角三角形,
∴∠ACB=90°.
∵点D是AB的中点,
∴CD=DB=1/2AB,
∴∠B=∠DCB=50°,
∴∠DCA=∠ACB-∠DCB=40°.
故∠DCA的度数为40°.
(2)4.8
(1)
∵AB=10,AC=6,BC=8,
∴AC²+BC²=6²+8²=100,AB²=10²=100,
∴AC²+BC²=AB²,
∴△ABC是直角三角形,
∴∠ACB=90°.
∵点D是AB的中点,
∴CD=DB=1/2AB,
∴∠B=∠DCB=50°,
∴∠DCA=∠ACB-∠DCB=40°.
故∠DCA的度数为40°.
(2)4.8
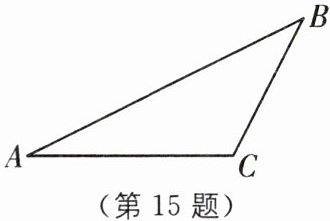
15 中考新考法 证明一般结论 如图,在△ABC 中,∠A,∠B,∠C 所对的边分别为 a,b,c.
(1)若 a= 6,b= 8,c= 12,请直接写出∠A 与∠B 的和与∠C 的大小关系;
(2)求证:△ABC 的内角和等于 180°;
(3)若$\frac{a}{a-b+c}= \frac{\frac{1}{2}(a+b+c)}{c}$,求证:△ABC 是直角三角形.
(1)若 a= 6,b= 8,c= 12,请直接写出∠A 与∠B 的和与∠C 的大小关系;
(2)求证:△ABC 的内角和等于 180°;
(3)若$\frac{a}{a-b+c}= \frac{\frac{1}{2}(a+b+c)}{c}$,求证:△ABC 是直角三角形.

答案:
(1)
∵在△ABC中,a=6,b=8,c=12,
∴∠A+∠B<∠C.
→当c²>a²+b²时,∠C为钝角
(2)如图,过点B作MN//AC.
∵MN//AC,
∴∠MBA=∠A,
∠NBC=∠C.

又∠MBA+∠ABC+∠NBC=180°,
∴∠A+∠ABC+∠C=180°.
即三角形三个内角的和等于180°.
(3)
∵a/(a - b + c)=(1/2(a + b + c))/c,
∴ac=1/2(a + b + c)·(a - b + c)=1/2[(a²+2ac+c²)-b²],
∴2ac=a²+2ac+c²-b²,
∴a²+c²=b².
故△ABC是直角三角形.
(1)
∵在△ABC中,a=6,b=8,c=12,
∴∠A+∠B<∠C.
→当c²>a²+b²时,∠C为钝角
(2)如图,过点B作MN//AC.
∵MN//AC,
∴∠MBA=∠A,
∠NBC=∠C.

又∠MBA+∠ABC+∠NBC=180°,
∴∠A+∠ABC+∠C=180°.
即三角形三个内角的和等于180°.
(3)
∵a/(a - b + c)=(1/2(a + b + c))/c,
∴ac=1/2(a + b + c)·(a - b + c)=1/2[(a²+2ac+c²)-b²],
∴2ac=a²+2ac+c²-b²,
∴a²+c²=b².
故△ABC是直角三角形.
查看更多完整答案,请扫码查看


