《2025年课时训练江苏人民出版社八年级数学上册苏科版》

1 (2025·南京秦淮区期中)如图,M,N 是∠AOB 的边 OA 上的两个点(OM＜ON),∠AOB= 30°,OM= a, MN= 3,若边 OB 上有且只有 1 个点 P,满足 △PMN 是等腰三角形,则 a 的取值范围是 .

答案：
a=3或a＞6 [解析]①作线段MN的垂直平分线交OB于点P，连接PM,PN,如图所示.

则PM=PN,此时△PMN是等腰三角形，过点M作MH⊥OB于点H，当MH＞MN,满足条件的点P恰好只有一个，
∵MN=3,∠AOB=30°.当MH=3时,OM=2MH=6，
∴当a＞6时，满足条件的点P恰好只有一个.②当△PMN是等边三角形时，满足条件的点P恰好只有一个,此时MN=MP,∠NMP=60°.
∵∠AOB=30°,
∴∠MPO=30°，
∴OM=MP=MN=3,
∴a=3.综上所述,满足条件的a的取值范围a=3或a＞6.

变式 1.1 (2025·连云港赣榆区期中)如图,在等腰三角形 ABC 中,AB= AC,∠B= 50°,D 为 BC 的中点,点 E 在 AB 上,∠AED= 69°,若点 P 是等腰三角形 ABC 的腰 AC 上的一点,则当△EDP 为等腰三角形时,∠EDP 的度数为100°或142°.

答案： 100°或142°

变式 1.2 (2025·常州金坛区期中)如图,∠POQ= 90°,点 A 是射线 OP 上定点,点 B 是射线 OQ 上动点 (点 B 不与点 O 重合),C 为 AB 的中点,连接 OC,将△AOC 沿直线 OC 翻折得△DOC,DO 交边 AB 于点 E,若△BOE 是等腰三角形,则∠BOE= 45或54 °.

答案： 45或54 [解析]
∵∠POQ=90°,点A是射线OP上定点,点B是射线OQ上动点(点B不与点O重合),C为AB的中点，
∴OC=AC=BC=$\frac{1}{2}$AB,
∴∠COA=∠CAO.
∵将△AOC沿直线OC翻折得△DOC，
∴由折叠的性质,得∠COA=∠COD，设∠COA=x,则∠CAO=∠COD=x，
∴∠BOE=90°-2x,∠OBA=90°-x,∠BEO=∠EOA+∠EAO=3x.①当BO=BE时,则∠BOE=∠BEO，
∴90°-2x=3x,解得x=18°,
∴∠BOE=54°.②当BO=EO时,则∠OBE=∠BEO，
∴90°-x=3x,解得x=22.5°，
∴∠BOE=45°.③当BE=OE时,则∠BOE=∠OBE，
∴90°-2x=90°-x,解得x=0°(不合题意,舍去).综上所述,∠BOE的度数为45°或54°.

变式 1.3 (2025·南通启东期中)如果两条线段将一个三角形分割成 3 个小等腰三角形,我们把这两条线段叫作这个三角形的"优美线".在△ABC 中, ∠B= 27°,AD 和 DE 是△ABC 的"优美线",点 D 在边 BC 上,点 E 在边 AC 上,且 AD= BD, DE= CE,则∠C 的度数为 .

答案：
18°或42° [解析]设∠C=x°,①当AD=AE时,如图
(1).

∵AD=BD,
∴∠B=∠BAD=27°.
∵DE=EC,
∴∠C=∠EDC=x°,
∴∠AED=2x°.
∵AD=AE,
∴∠ADE=∠AED=2x°，
∴2x+x=27°+27°,
∴x=18°.②当AD=DE时,如图
(2).

同理∠B=∠BAD=27°,∠C=∠EDC=x°,∠DAE=∠AED=2x°，
∴27°+27°+2x+x=180°,
∴x=42°.③当EA=DE时,
∵90°-x+27°+27°+x=180°，
∴x不存在,应舍去.综上所述,满足条件的∠C的度数为18°或42°.

2 如图,AB= 12,C 为边 AB 上一动点(不与点 A,B 重合),以 AC 为边在 AB 的上方作等边三角形 ACD,过点 C 作 CD 的垂线,E 为垂线上任意一点,连接 DE,F 为 DE 的中点,连接 BF,则 BF 的最小值是 .

答案：
6 [解析]如图,连接AF,CF,设交CD于点H.
∵DC⊥EC,
∴∠DCE=90°.
∵F为DE的中点,
∴CF=DF.
∵△ACD为等边三角形，
∴∠CAD=60°,AC=AD.在△ACF和△ADF中,$\left\{\begin{array}{l} AC=AD,\\ CF=DF,\\ AF=AF,\end{array}\right. $
∴△ACF≌△ADF(SSS)，
∴∠CAF=∠DAF=30°,
∴AH⊥CD.当BF⊥AF时,BF的值最小,如图所示,设点F'为垂足，

在Rt△AF'B中,AB=12,∠BAF'=30°,
∴BF=6.

变式 2.1 (2025·南京外国语学校期中)如图,点 E 在等边三角形 ABC 的边 BC 上,BE= 8,射线 CD⊥ BC,垂足为 C,点 P 是射线 CD 上一动点,点 F 是线段 AB 上一动点,当 EP+FP 的值最小时, BF= 10,则 AF 的长为(B).
A.3
B.4
C.5
D.6

答案： B

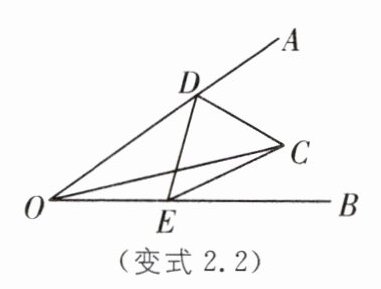
变式 2.2 (2025·苏州松陵一中月考)如图,已知 ∠AOB= α,C 是∠AOB 内部的一点,且 OC= 3, 点 D,E 分别是 OA,OB 上的动点,若△CDE 周长的最小值等于 3,则 α= ( ).


A.45°
B.40°
C.35°
D.30°

答案：
D [解析]如图,作点C关于OA的对称点P,关于OB的对称点F,连接PF,交OA于D,OB于E.此时,△CDE的周长最小.连接OP,OF,CD,EF.
∵点C与点P关于OA对称，
∴OA垂直平分PC，
∴∠POA=∠AOC,PD=CD,OC=OP，同理,可得∠FOB=∠BOC，EF=CE,OF=OC，
∴∠POF=2α.
∵△CDE的周长=CD+DE+EC=PD+EF+ED=PF=3，且OP=OC=OF=3,
∴△POF是等边三角形，
∴2α=60°,
∴α=30°.故选D.