第77页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘 B处离桌面的高度 BC 为7 cm,此时底部边缘 A处与C处间的距离 AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D 是 B 的对应点),顶部边缘 D 处到桌面的距离 DE 为20 cm,则底部边缘 A 处与 E 之间的距离 AE 为(
A.15 cm
B.18 cm
C.21 cm
D.24 cm
A
).A.15 cm
B.18 cm
C.21 cm
D.24 cm
答案:
A
2 新情境 通过限高隧道 一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于(
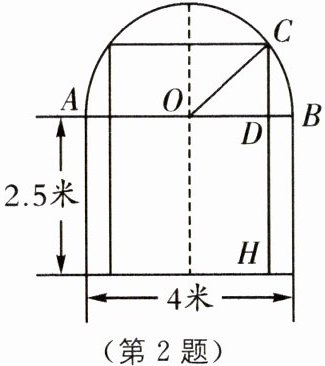
A.4.1米
B.4.0米
C.3.9米
D.3.8米
A
).
A.4.1米
B.4.0米
C.3.9米
D.3.8米
答案:
A
如图,某自动感应门的正上方装着一个感应器 A,离地距离 AB= 2米,当人体进入感应范围内时,感应门就会自动打开,一个身高1.5米的学生CD 刚走到离门间距 CB= 1.2米的地方时,感应门自动打开,则该感应器感应长度 AD 为(
A.1.2米
B.1.3米
C.1.5米
D.2米
B
).A.1.2米
B.1.3米
C.1.5米
D.2米
答案:
B
4 跨学科 发声物体的振动 (2025·盐城期中)小丽在物理课上学习了发声物体的振动实验后,对其做了进一步的探究:在一个支架的横杆点 O 处用根细绳悬挂一个小球 A,小球 A 可以自由摆动,如图,OA 表示小球静止时的位置.当小丽用发声物体靠近小球时,小球从 OA 摆到 OB 位置,此时过点 B 作 BC⊥OA 于点 C(图中的 A,B,O,C 在同一平面上),测得 AC= 2 cm,BC= 8 cm.求 OB 的长.


答案:
设OB=xcm.
∵AC=2cm,
∴OC=OA−AC=OB−AC=(x−2)cm.
∵BC⊥OA,
∴在Rt△OBC中,OB²=BC²+OC²,即x²=8²+(x−2)²,解得x=17.故OB的长为17cm.
∵AC=2cm,
∴OC=OA−AC=OB−AC=(x−2)cm.
∵BC⊥OA,
∴在Rt△OBC中,OB²=BC²+OC²,即x²=8²+(x−2)²,解得x=17.故OB的长为17cm.
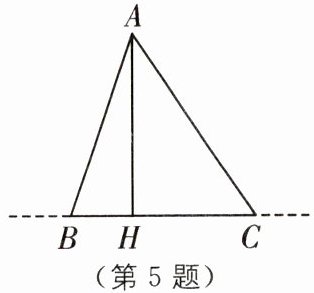
5 教材 P98例1·变式 如图,点 A 是网红打卡地诗博园,市民可在云龙湖边的游客观光车站 B 或C 处乘车前往,且 AB= BC,因市政建设,点 C到点 A 段现暂时封闭施工,为方便出行,在湖边的 H 处修建了一临时车站(点 H 在线段 BC上),由 H 处亦可直达 A 处,若 AC= 1 km,AH= 0.8 km,CH= 0.6 km.
(1)判断△ACH 的形状,并说明理由;
(2)求路线 AB 的长.
(1)判断△ACH 的形状,并说明理由;
(2)求路线 AB 的长.

答案:
(1)△ACH是直角三角形.理由如下:
∵AC=1km,AH=0.8km,CH=0.6km,
∴AC²=AH²+CH²,
∴△ACH是直角三角形.
(2)
∵△ACH是直角三角形,
∴AH⊥BC.设AB=BC=xkm,则BH=BC−HC=(x−0.6)km,由勾股定理,得AB²=AH²+BH²,即x²=0.8²+(x−0.6)²,解得x=$\frac{5}{6}$.故路线AB的长为$\frac{5}{6}$km.
(1)△ACH是直角三角形.理由如下:
∵AC=1km,AH=0.8km,CH=0.6km,
∴AC²=AH²+CH²,
∴△ACH是直角三角形.
(2)
∵△ACH是直角三角形,
∴AH⊥BC.设AB=BC=xkm,则BH=BC−HC=(x−0.6)km,由勾股定理,得AB²=AH²+BH²,即x²=0.8²+(x−0.6)²,解得x=$\frac{5}{6}$.故路线AB的长为$\frac{5}{6}$km.
查看更多完整答案,请扫码查看


