《2025年课时训练江苏人民出版社八年级数学上册苏科版》

1 如图,点 C 在线段 AB 上,$AD// EB$,$∠ADC= ∠BCE$,$AC= BE$.求证:$△ACD\cong △BEC$.

答案：
∵AD//BE,
∴∠A=∠B.在△ACD 和△BEC 中,{∠A=∠B,∠ADC=∠BCE,AC=BE,
∴△ACD≌△BEC(AAS).

2 (2025·镇江丹徒区期末)如图,已知 A,D 是 CF 上的两点,且$AB= DE$,$AB// DE$,$AF= CD$.求证:
(1)$△ABC\cong △DEF$;
(2)$BC// EF$.

答案：
(1)
∵AB//DE,
∴∠BAC=∠EDF.
∵AF=CD,
∴AF+AD=CD+AD,即 DF=AC.在△ABC 和△DEF 中,{AB=DE,∠BAC=∠EDF,AC=DF,
∴△ABC≌△DEF(SAS).
(2)
∵△ABC≌△DEF,
∴∠C=∠F,
∴BC//EF.

3 如图,已知$∠BDC= ∠CEB= 90^{\circ }$,BE,CD 交于点 O,且 AO 平分$∠BAC$.求证:$OB= OC$.

答案：
∵∠BDC=∠CEB=90°,
∴∠ADO=∠AEO=90°.
∵AO 平分∠BAC,
∴∠DAO=∠EAO.在△DAO 和△EAO 中,{∠ADO=∠AEO,∠DAO=∠EAO,AO=AO,
∴△DAO≌△EAO(AAS).
∴OD=OE.在△BDO 和△CEO 中,{∠BDO=∠CEO,OD=OE,∠DOB=∠EOC,
∴△BDO≌△CEO(ASA),
∴OB=OC.

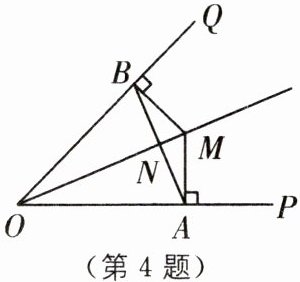
4 如图,OM 平分$∠POQ$,$MA⊥OP$,$MB⊥OQ$,A,B 为垂足,AB 交 OM 于点 N.求证:$∠OAB= ∠OBA$.

答案：
∵MA⊥OP,MB⊥OQ,
∴∠OBM=∠OAM=90°.
∵OM 平分∠POQ,
∴∠BOM=∠AOM.又 OM 是△OBM 和△OAM 的公共边,
∴△OBM≌△OAM(AAS).
∴OB=OA,∠BOM=∠AOM.
∵ON=ON,
∴△OBN≌△OAN(SAS),
∴∠OAB=∠OBA.