第8页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 教材 P13 练习 T3·变式 (2025·广东阳江城区期末改编)如图,△DBC≌△ECB,且 BE 与 CD 相交于点 A,下列结论错误的是(
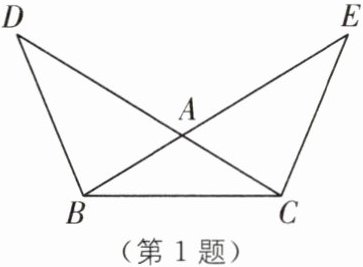
A.BE= CD
B.∠ABD= ∠ACE
C.∠D= ∠E
D.BD= AE
D
).
A.BE= CD
B.∠ABD= ∠ACE
C.∠D= ∠E
D.BD= AE
答案:
D
如图,△ABC≌△ADE,点 D 在 BC 边上,∠E= 35°,∠DAC= 30°,则∠BDA 的度数为(
A.35°
B.40°
C.50°
D.65°
D
).A.35°
B.40°
C.50°
D.65°
答案:
D
3 教材 P12 例·改编 (2025·湖南长沙浏阳期末)如图,点 B,C 在 AD 上,△ACE≌△DBF,AD= 8,BC= 4,则 AB 的长为(
A.1.5
B.2
C.3
D.4
B
).
A.1.5
B.2
C.3
D.4
答案:
B
4 如图,将△ABC 沿 BC 方向平移 1 cm 得到△DEF,若△ABC 的周长等于 10 cm,则四边形 ABFD 的周长等于
12 cm
.
答案:
12 cm
在△ABC 中,∠A= 30°,∠B= 70°,且△ABC≌△DEF,则∠F 的度数为
80°
.
答案:
80°
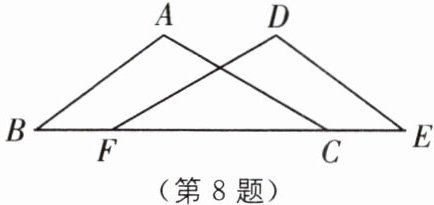
6 新情境 成功发射神舟十五号 (2025·河南南阳邓州期中)为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足△ABD≌△ACE,点 B 和点 C 是对应顶点,若 AB= 8 cm,AD= 3 cm,则 DC= ______cm.

5
答案:
5
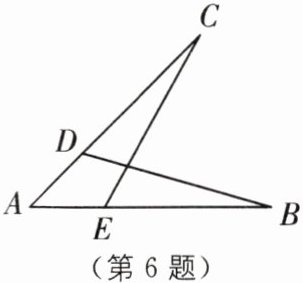
7 教材 P14 习题 T4·变式 (2024·湖南长沙期末)如图,两个三角形是全等三角形,则 x 的值是
30
.
答案:
30
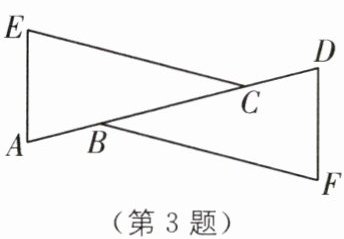
8 (2024·徐州期中)如图,点 B,F,C,E 在同一条直线上,△ABC≌△DEF,AB= 6,BC= 11,BF= 3,∠ACB= 30°.求∠DFE 的度数及 DE,CE 的长.

答案:
∵△ABC≌△DEF,AB=6,BC=11,∠ACB=30°,
∴∠ACB=∠DFE=30°,AB=DE=6,BC=EF=11,
∴BC-CF=EF-CF,即 BF=CE.
∵BF=3,
∴CE=3.
故∠DFE=30°,DE=6,CE=3.
∵△ABC≌△DEF,AB=6,BC=11,∠ACB=30°,
∴∠ACB=∠DFE=30°,AB=DE=6,BC=EF=11,
∴BC-CF=EF-CF,即 BF=CE.
∵BF=3,
∴CE=3.
故∠DFE=30°,DE=6,CE=3.
9 (2024·广西桂林临桂区期中)如图,△ABD≌△EBC,AB= 2 cm,BC= 5 cm.
(1)求 DE 的长.
(2)若 A,B,C 在一条直线上,则 DB 与 AC 垂直吗?为什么?
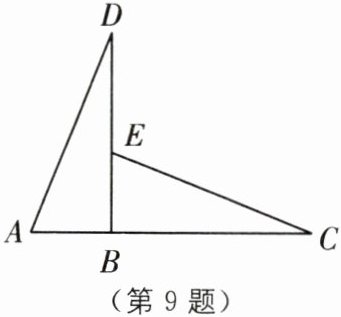
(1)求 DE 的长.
(2)若 A,B,C 在一条直线上,则 DB 与 AC 垂直吗?为什么?

答案:
(1)
∵△ABD≌△EBC,BC=5 cm,AB=2 cm,
∴BD=BC=5 cm,AB=EB=2 cm,
∴DE=BD-BE=3 cm.
(2)DB 与 AC 垂直.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC.
又 A,B,C 在一条直线上,
∴∠EBC+∠ABD=180°,
∴∠ABD=∠EBC=90°,
∴DB 与 AC 垂直.
(1)
∵△ABD≌△EBC,BC=5 cm,AB=2 cm,
∴BD=BC=5 cm,AB=EB=2 cm,
∴DE=BD-BE=3 cm.
(2)DB 与 AC 垂直.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC.
又 A,B,C 在一条直线上,
∴∠EBC+∠ABD=180°,
∴∠ABD=∠EBC=90°,
∴DB 与 AC 垂直.
查看更多完整答案,请扫码查看


