第32页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 教材 P36 练习 T1·改编(2025·上海黄浦区期中)到三角形三个顶点距离都相等的点是(
A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
B
).A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
答案:
B
2 教材 P35 讨论·变式 如图,AC= AD,BC= BD,则下列判断正确的是(
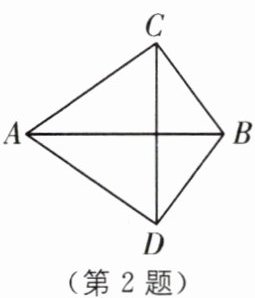
A.CD 平分∠ACB
B.AB 平分∠CAD
C.CD 垂直平分 AB
D.AB 与 CD 互相垂直平分
B
).
A.CD 平分∠ACB
B.AB 平分∠CAD
C.CD 垂直平分 AB
D.AB 与 CD 互相垂直平分
答案:
B
3 教材 P39 习题 T2·改编(2025·南通海门区期中)如图,在△ABC 中,∠C= 90°,AC= 3,BC= 4,AB= 5,分别以 A,B 为圆心,AC 为半径画弧,两弧分别交于 E,F,直线 EF 交 BC 于点 D,连接 AD,则△ACD 的周长等于(
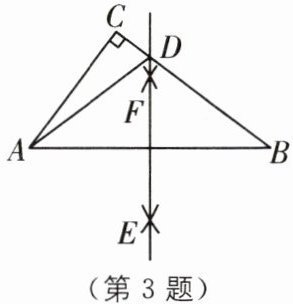
A.7
B.8
C.9
D.$\frac{17}{2}$
A
).
A.7
B.8
C.9
D.$\frac{17}{2}$
答案:
A
4 (2025·南京鼓楼区期中)如图,AB= AC,DB= DC,点 E 在 AD 上,求证:EB= EC.
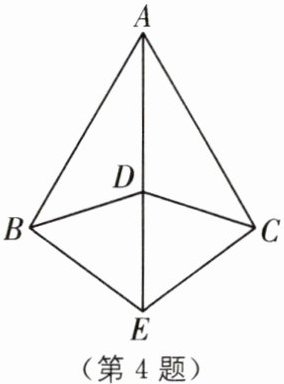

答案:
∵AB=AC,DB=DC,
∴AD 是线段 BC 的垂直平分线.
∵点 E 在 AD 上,
∴EB=EC.
归纳总结 本题考查的是线段的垂直平分线的性质和判定,掌握线段的垂直平分线上的点到线段的两个端点的距离相等和到线段的两个端点的距离相等的点在线段的垂直平分线上是解题的关键.
∵AB=AC,DB=DC,
∴AD 是线段 BC 的垂直平分线.
∵点 E 在 AD 上,
∴EB=EC.
归纳总结 本题考查的是线段的垂直平分线的性质和判定,掌握线段的垂直平分线上的点到线段的两个端点的距离相等和到线段的两个端点的距离相等的点在线段的垂直平分线上是解题的关键.
5 在如图所示的方格纸中,每个小方格都是边长为 1 的正方形,A,B 是方格纸中的两个格点. 若要找出格点 C,使 AC= BC,则满足条件的格点 C 有
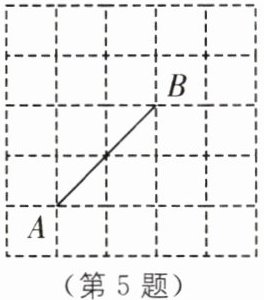
5
个.
答案:
5
6 教材 P39 习题 T3·改编(2025·广东广州期中)如图,在△ABC 中,AB= AC.
(1)利用尺规,作 AB 边的垂直平分线交 AC 于点 D,交 AB 于点 E;(不写作法,保留作图痕迹)
(2)在(1)中,连接 BD,若 BC= 6,AB= 8,求△BDC 的周长.
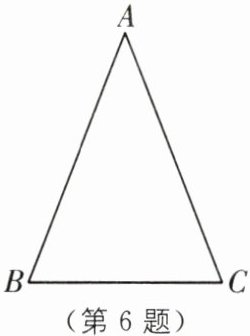
(1)利用尺规,作 AB 边的垂直平分线交 AC 于点 D,交 AB 于点 E;(不写作法,保留作图痕迹)
(2)在(1)中,连接 BD,若 BC= 6,AB= 8,求△BDC 的周长.

答案:
(1)如图所示,直线 DE 即为所求.
(2)
∵DE 垂直平分 AB,
∴AD=BD,
∴△BCD 的周长为 BD+CD+BC=AD+CD+BC=AC+BC=8+6=14.

(1)如图所示,直线 DE 即为所求.
(2)
∵DE 垂直平分 AB,
∴AD=BD,
∴△BCD 的周长为 BD+CD+BC=AD+CD+BC=AC+BC=8+6=14.

7 教材 P41 习题 T10·改编 某市政府计划修建一处公共服务设施,使它到三所公寓 A,B,C 的距离相等.
(1)若三所公寓 A,B,C 的位置如图所示,请你在图中确定这处公共服务设施(用点 P 表示)的位置(尺规作图,保留作图痕迹,不写作法);
(2)若∠BAC= 77°,求∠BPC 的度数.
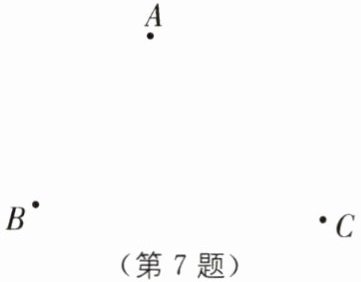
(1)若三所公寓 A,B,C 的位置如图所示,请你在图中确定这处公共服务设施(用点 P 表示)的位置(尺规作图,保留作图痕迹,不写作法);
(2)若∠BAC= 77°,求∠BPC 的度数.

答案:
(1)如图,点 P 即为所求.
(2)如图,连接 PA,PB,PC,BC.
∵点 P 在线段 AB,AC 的垂直平分线上,
∴PA=PB=PC,
∴∠PBA=∠PAB,∠PCA=∠PAC,
∴∠PBC+∠PCB=180°-∠PBA-∠BAC-∠PCA=180°-2∠BAC=180°-2×77°=26°,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-26°=154°.
素养考向 本题考查作图—应用与设计、线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.

(1)如图,点 P 即为所求.
(2)如图,连接 PA,PB,PC,BC.
∵点 P 在线段 AB,AC 的垂直平分线上,
∴PA=PB=PC,
∴∠PBA=∠PAB,∠PCA=∠PAC,
∴∠PBC+∠PCB=180°-∠PBA-∠BAC-∠PCA=180°-2∠BAC=180°-2×77°=26°,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-26°=154°.
素养考向 本题考查作图—应用与设计、线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.

查看更多完整答案,请扫码查看


