第53页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
10 (2025·广东肇庆高要区期末)如图,要测量河两岸相对的两点A,B的距离,可在河的一侧取AB的垂线BM上两点C,D,使BC= CD,再画出BM的垂线DE,使E在AC的延长线上,若BD= 10 m,DE= 12 m,CE= 13 m,则A,B两点的距离是(
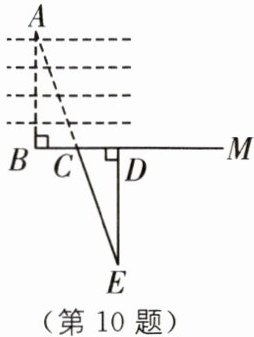
A.5 m
B.10 m
C.12 m
D.13 m
C
).
A.5 m
B.10 m
C.12 m
D.13 m
答案:
C
11 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图(1),在△ABC中,∠B= 2∠C,线段AC的垂直平分线交AC于点D,交BC于点E. 求证:AE是△ABC的一条特异线;
(2)如图(2),若△ABC是特异三角形,∠A= 30°,∠B为钝角,求出所有可能的∠B的度数.
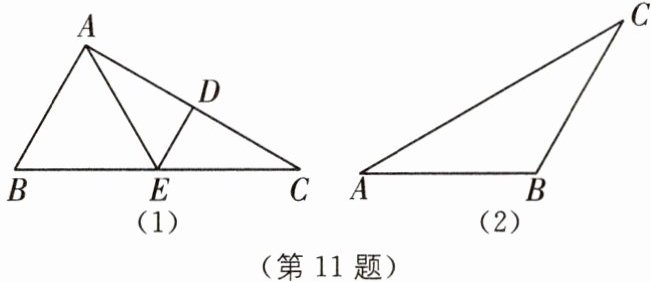
(1)如图(1),在△ABC中,∠B= 2∠C,线段AC的垂直平分线交AC于点D,交BC于点E. 求证:AE是△ABC的一条特异线;
(2)如图(2),若△ABC是特异三角形,∠A= 30°,∠B为钝角,求出所有可能的∠B的度数.

答案:
(1)
∵DE是线段AC的垂直平分线,
∴EA = EC,即△EAC是等腰三角形,
∴∠EAC = ∠C,
∴∠AEB = ∠EAC + ∠C = 2∠C.
又∠B = 2∠C,
∴∠AEB = ∠B,
∴△EAB是等腰三角形,
∴AE是△ABC的一条特异线.
(2)当BD是特异线时,
如图
(1),若AB = BD = DC,则∠ABC = ∠ABD + ∠DBC = 120° + 15° = 135°;
如图
(2),若AD = AB,DB = DC,则∠ABC = ∠ABD + ∠DBC = 75° + 37.5° = 112.5°;
如图
(3),若AD = DB,DC = CB,则∠ABC = ∠ABD + ∠DBC = 30° + 60° = 90°(舍去);
当AD是特异线时,如图
(4),若AB = BD,AD = DC,则∠ABC = 180° - 20° - 20° = 140°;
当CD为特异线时,不合题意.
综上所述,符合条件的∠ABC的度数为135°或112.5°或140°.
(1)
∵DE是线段AC的垂直平分线,
∴EA = EC,即△EAC是等腰三角形,
∴∠EAC = ∠C,
∴∠AEB = ∠EAC + ∠C = 2∠C.
又∠B = 2∠C,
∴∠AEB = ∠B,
∴△EAB是等腰三角形,
∴AE是△ABC的一条特异线.
(2)当BD是特异线时,
如图
(1),若AB = BD = DC,则∠ABC = ∠ABD + ∠DBC = 120° + 15° = 135°;
如图
(2),若AD = AB,DB = DC,则∠ABC = ∠ABD + ∠DBC = 75° + 37.5° = 112.5°;
如图
(3),若AD = DB,DC = CB,则∠ABC = ∠ABD + ∠DBC = 30° + 60° = 90°(舍去);
当AD是特异线时,如图
(4),若AB = BD,AD = DC,则∠ABC = 180° - 20° - 20° = 140°;
当CD为特异线时,不合题意.
综上所述,符合条件的∠ABC的度数为135°或112.5°或140°.
12 跨学科 声音的产生 小亮同学在物理课上学习了发声物体的振动实验后,对其做了进一步的探究:如图(1),在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,摆动过程中绳子的伸长不考虑且绳子始终是绷直的. 如图,OA表示小球静止时的位置. 当小明用发声物体靠近小球时,如图(2),小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,过点C作CE⊥OA于点E,测得BD= 7 cm,OE= 7 cm. (图中的A,B,O,C在同一平面上),求证此时OB⊥OC.
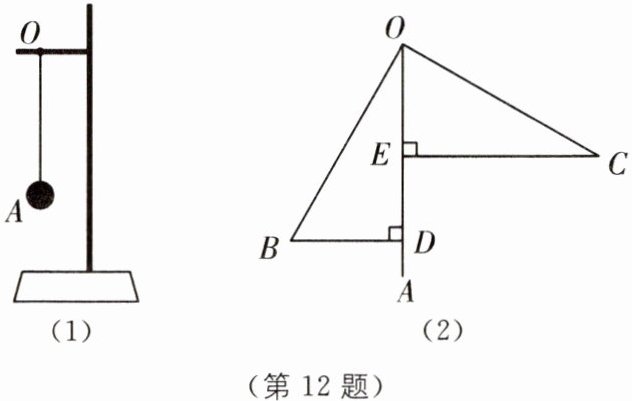

答案:
∵BD⊥OA,CE⊥OA,
∴∠OEC = ∠ODB = 90°,
∴∠B + ∠BOD = 90°.
∵BD = 7cm,OE = 7cm,
∴BD = OE,
∴Rt△OBD≌Rt△COE(HL),
∴∠B = ∠COE,
∴∠COE + ∠BOD = 90°,
即∠BOC = 90°,
∴OB⊥OC.
∵BD⊥OA,CE⊥OA,
∴∠OEC = ∠ODB = 90°,
∴∠B + ∠BOD = 90°.
∵BD = 7cm,OE = 7cm,
∴BD = OE,
∴Rt△OBD≌Rt△COE(HL),
∴∠B = ∠COE,
∴∠COE + ∠BOD = 90°,
即∠BOC = 90°,
∴OB⊥OC.
查看更多完整答案,请扫码查看


