第71页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 教材 P86问题·改编 (2025·连云港赣榆区期中)如图,三个正方形围成一个直角三角形,图中的数据是它们的面积,则正方形 A 的面积为(
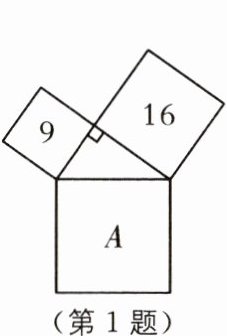
A.9
B.16
C.25
D.5
C
).
A.9
B.16
C.25
D.5
答案:
C
2 (2025·苏州姑苏区期中)如图,在Rt△ABC中,分别以这个三角形的三边为边长作正方形,面积分别记为$S_1,S_2,S_3,$若$S_1+S_3-S_2= 20,$则阴影部分面积为(
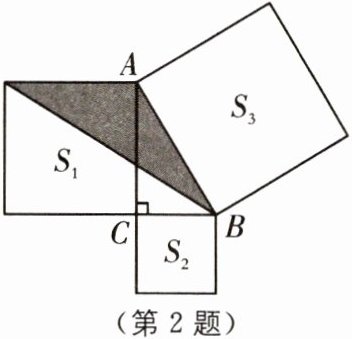
A.10
B.5
C.20
D.15
B
).
A.10
B.5
C.20
D.15
答案:
B
(1)若a= 6,b= 8,则c=
(2)若a= 40,c= 41,则b=
(3)若c= 26,a:b= 5:12,则a=
10
;(2)若a= 40,c= 41,则b=
9
;(3)若c= 26,a:b= 5:12,则a=
10
,b= 24
.
答案:
(1)10
(2)9
(3)10 24
(1)10
(2)9
(3)10 24
在Rt△ABC中,∠C= 90°.若BC= 9,AC= 12,则AB=
15
.
答案:
15
5 (2025·山东济南钢城区期末)勾股定理是数学中一颗璀璨的明珠,在人类的文明史上有杰出的贡献.如图(1),在Rt△ABC中,∠ACB= 90°,BC= 3,分别以Rt△ABC的各边为一边向Rt△ABC外部作正方形,把两个较小的正方形按图(2)放置,若图形①的面积是4,则图形②的面积是______
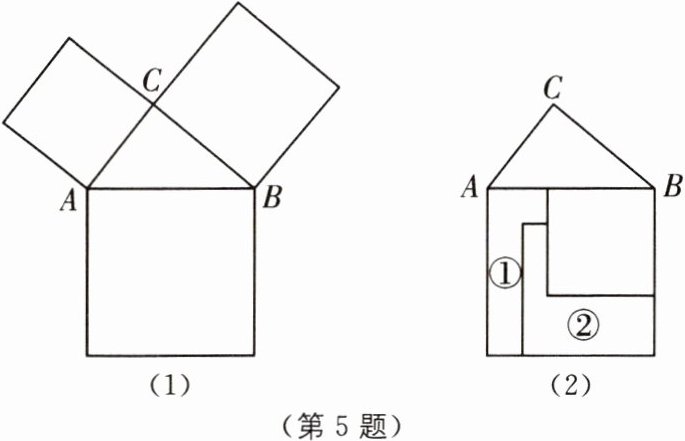
5
.
答案:
5
6 方程思想 (2024·苏州昆山月考)在Rt△ABC中,∠C= 90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)若a:b= 3:4,c= 10,求a,b的值;
(2)若c-a= 4,b= 16,求a的值.
(1)若a:b= 3:4,c= 10,求a,b的值;
(2)若c-a= 4,b= 16,求a的值.
答案:
(1)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a:b=3:4,
∴设a=3x,则b=4x.
∵a²+b²=c²,即(3x)²+(4x)²=10²,
解得x=2(负值舍去),
∴a=3x=6,b=4x=8.
求解之后要根据实际情况对值进行取舍
(2)在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
∴a²+b²=c².
∵c−a=4,b=16,
∴a²+16²=(a+4)²,解得a=30.
(1)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a:b=3:4,
∴设a=3x,则b=4x.
∵a²+b²=c²,即(3x)²+(4x)²=10²,
解得x=2(负值舍去),
∴a=3x=6,b=4x=8.
求解之后要根据实际情况对值进行取舍
(2)在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
∴a²+b²=c².
∵c−a=4,b=16,
∴a²+16²=(a+4)²,解得a=30.
7 (2025·扬州江都区期中)如图,在Rt△ABC中,已知∠A= 90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证$:BE^2-AE^2= AC^2;$
(2)若AC= 6,BD= 5,求AE的长.
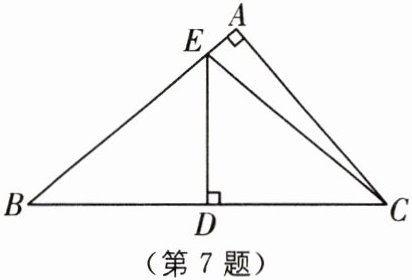
(1)求证$:BE^2-AE^2= AC^2;$
(2)若AC= 6,BD= 5,求AE的长.

答案:
(1)
∵DE⊥BC,D是斜边BC的中点,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理,可得CE²=AC²+AE²,
∴BE²=AC²+AE²,
∴BE²−AE²=AC².
(2)
∵BD=5,D是斜边BC的中点,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理,可得AB=8,
∴AB=BE+AE=8.
设AE=x,则BE=CE=8−x,
在Rt△ACE中,由勾股定理可得CE²=AC²+AE²,
即(8−x)²=6²+x²,解得x=$\frac{7}{4}$,即AE=$\frac{7}{4}$.
(1)
∵DE⊥BC,D是斜边BC的中点,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理,可得CE²=AC²+AE²,
∴BE²=AC²+AE²,
∴BE²−AE²=AC².
(2)
∵BD=5,D是斜边BC的中点,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理,可得AB=8,
∴AB=BE+AE=8.
设AE=x,则BE=CE=8−x,
在Rt△ACE中,由勾股定理可得CE²=AC²+AE²,
即(8−x)²=6²+x²,解得x=$\frac{7}{4}$,即AE=$\frac{7}{4}$.
查看更多完整答案,请扫码查看


